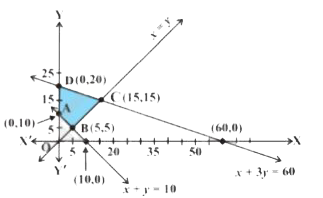
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum?
Point B
Point C
Point D
every point on the line segment CD
The correct Answer is:C
Step by step video & image solution for Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CBSE TERM -1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM -1 SAMPLE PAPER 1EXERCISE - SECTION - B
20 Videos
- CBSE TERM -1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM -1 SAMPLE PAPER 1EXERCISE - SECTION - C
4 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION - C
9 Videos
- SAMPLE PAPER (SELF-ASSESSMENT) -10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF-ASSESSMENT) -10EXERCISE - SECTION - C
5 Videos
Similar Questions
Knowledge Check
In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
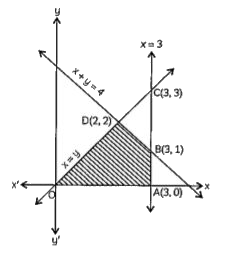 AOBBCCDD
AOBBCCDDConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
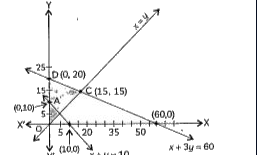
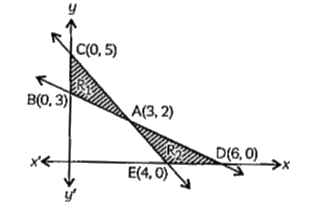
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IVThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R1 is the feasible region, and the ojective function is Z1=2x−y, then the maximum value of Z1 occurs at:
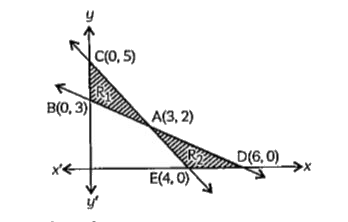 A(0,5)B(0,3)C(3,2)D(6,0)
A(0,5)B(0,3)C(3,2)D(6,0)
In the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
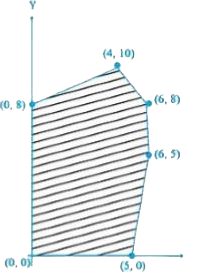
View SolutionThe shaded part of the given figure indicates the feasible region
Then the constraints are
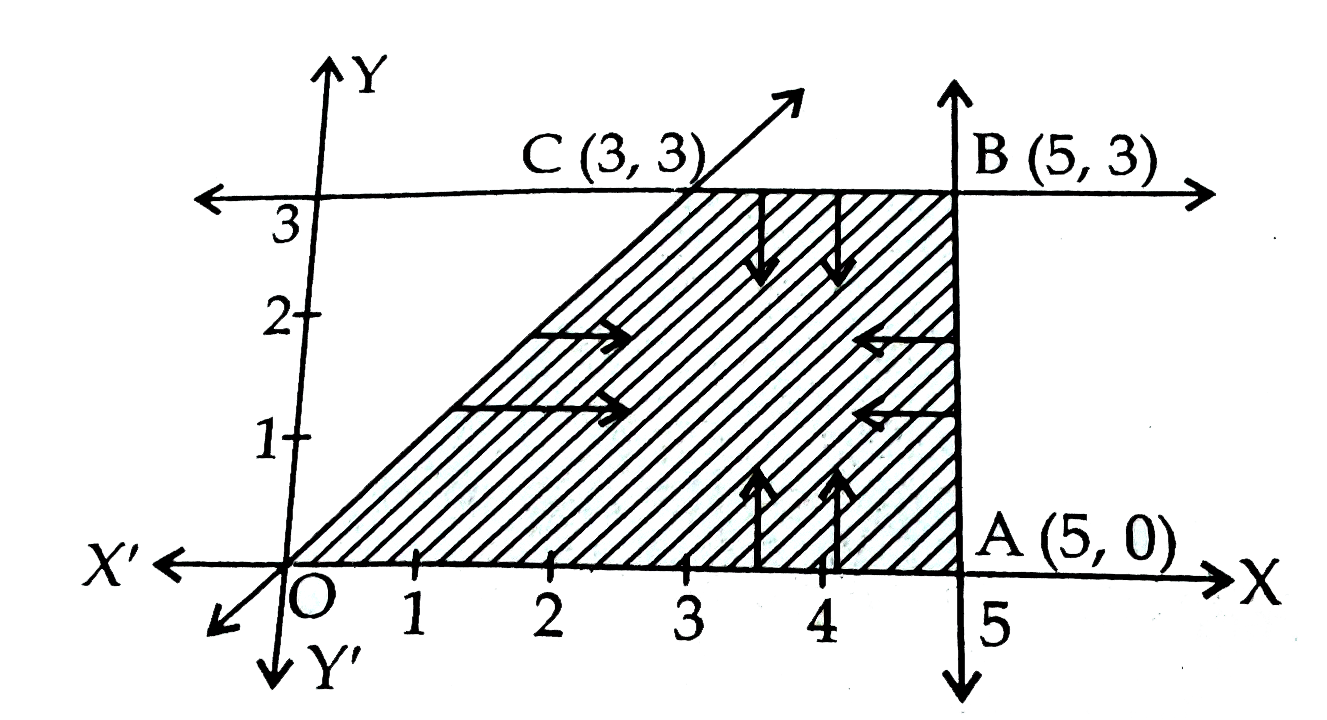
View SolutionThe shaded part of the given figure indicates the feasible region
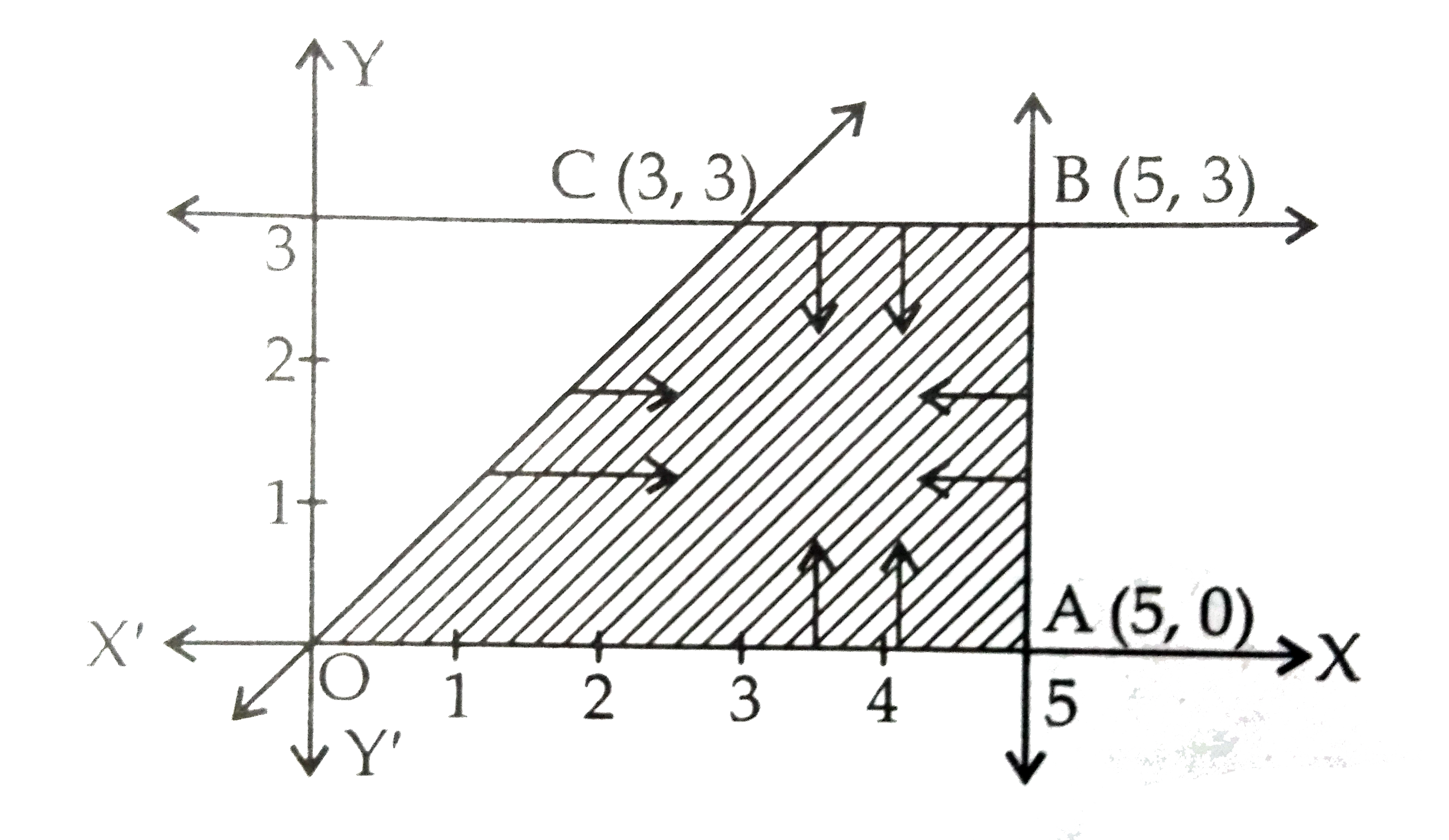
Then the constraints are
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:
View Solution