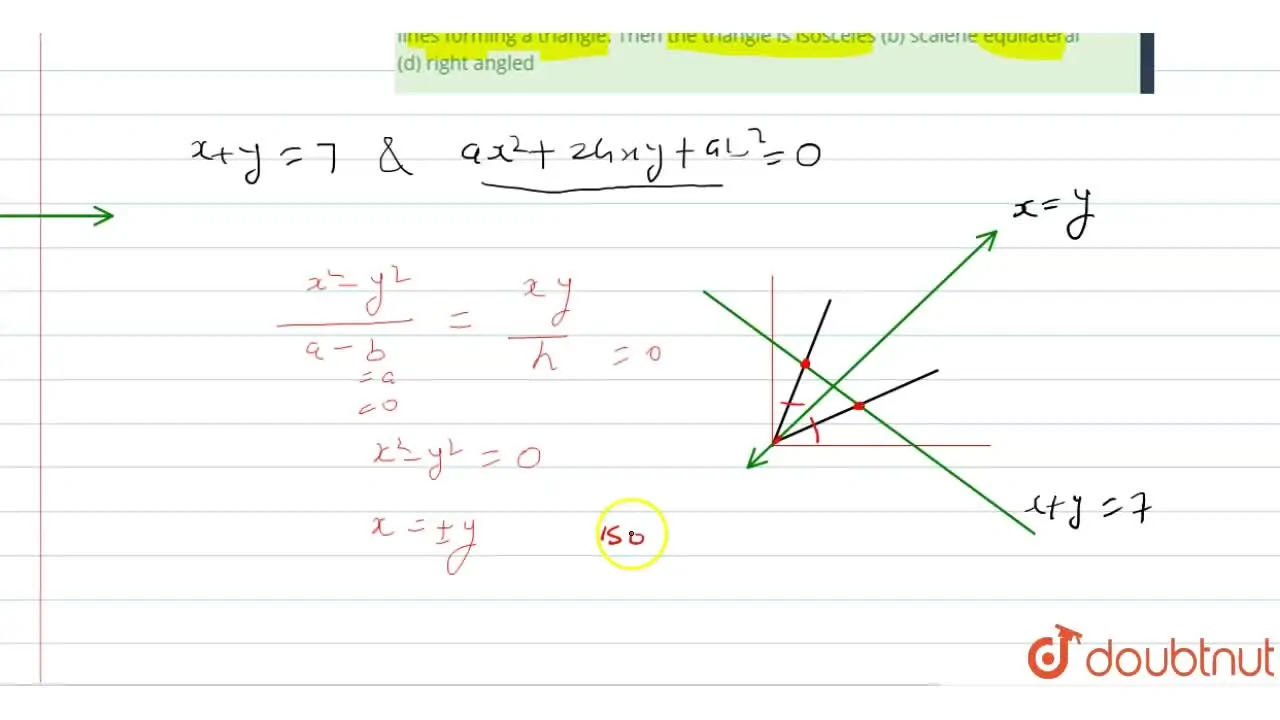
x+y=7 and ax2+2hxy+ay2=0,(a≠0) , are three real distinct lines forming a triangle. Then the triangle is isosceles (b) scalene equilateral (d) right angled
isosceles
scalene
equilateral
right - angled
The correct Answer is:1
ax2+2hxy+ay2=0. Is symmetrical about y=x.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Multiple Correct Answer Type9videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Linked Comprehension Type6videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.27videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Matching Column Type1videos
PARABOLA
Similar Questions
x+y=7 and ax2+2hxy+ay2=0,(a≠0) , are three real distinct lines forming a triangle. Then the triangle is (a) isosceles (b) scalene equilateral (d) right angled
View SolutionThe straight lines x+y=0,3x+y−4=0andx+3y−4=0 form a triangle which is (A) isosceles (B) right angled (C) equilateral (D) scalene
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionCan an equilateral triangle be a, an acute-,b. a right-, and c. an obtuse-angled triangle ? What about isosceles and scalene triangles ?
View SolutionWrite the coordinates of the orthocentre of the triangle formed by the lines xy=0 and x+y=1.
View Solution. The lines (a+b)x+(a−b)y−2ab=0,(a−b)x+(a+b)y−2ab=0andx+y=0 form an isosceles triangle whose vertical angle is
View Solution. The lines (a+b)x+(a−b)y−2ab=0,(a−b)x+(a+b)y−2ab=0andx+y=0 form an isosceles triangle whose vertical angle is
View SolutionShow that the straight lines x2+4xy+y2=0 and the line x-y=4 form an equilateral triangle .
View Solution
The triangle formed by complex numbers z,iz,i2z is
(a)Equilateral
(b) Isosceles
(c)Right angle
(d) ScaleneView SolutionShow that the common tangents to the parabola y2=4x and the circle x2+y2+2x=0 form an equilateral triangle.
View Solution