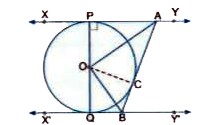
XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
In △OPA and △OCA
OP=OC (Radii of the same circle)
AP=AC (Tangent from point A)
AO=AO (Common side)
By SSS congruency, △OPA and △OCA are congruent.
Thus, ∠POA=∠COA
Similarly, we can show
∠QOB=∠COB
Since POQ is a diameter of the circle, it is a straight line. Thus,
∠POA+∠COA+∠COB+∠QOB=180∘
2∠COA+2∠COB=180∘
∠COA+∠COB=90∘
∠AOB=90∘
Similar Questions
In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
 View Solution
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View Solution
Knowledge Check
- Question 1 - Select One
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘ - Question 2 - Select One
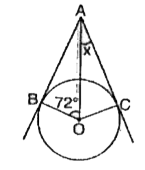
TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘ - Question 3 - Select One
AB and AC are tangents to the circle with centre O. Then x equals.
 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘
landm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
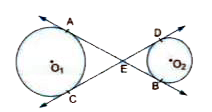
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
 View Solution
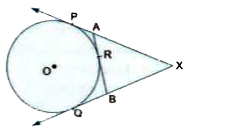
View SolutionIn Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
 View Solution
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View SolutionAB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the ∠BDOis
View Solution

