XY is a diameter of a circle. PAQ is a tangent to the circle at the point A lying on the circumference. The perpendicular drawn on the tangent to the circle from X intersects PAQ at Z. Prove that XA is a bisector of ∠YXZ. [GP−X]Solution in Bengali
Let XY be a diameter of the circle with centre at O. PAQ is a tangent to the circel at point A. The perpendicular XZ drawn from X to PAQ intersects PAQ at Z.
To prove : XA is a bisector of ∠YXZ,i.e.,∠YXA=∠ZXA
Construction : Let us join O, A.
Proof : PAQ is a tangent to the circle with centre O at the point A and OA is radius passing through point pf contact A.
∴OA⊥PAQ [by theorem -40]
∴∠OAP=90∘or,∠OAZ=90∘........(1)
Again given that XZ⊥PAQ,∴∠XZA=90∘....(2)
From (1) and (2) we get, XZ∣∣OAandXA is their transversal ∴∠OAX=∠ZXA.....(3)
[∵ alternate angles]
or,∠ZXA=∠AXO[∵OX=OA= radii of same circle]
or∠ZXA=∠YXA
Hence XA is the bisector of ∠YXZ. (Proved)

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View Solutionमाना कि केंद्र बिन्दु O वाले वृत्त पर P और Q दो बिन्दू है । यदि वृत्त के दो बिन्दू P और Q से होकर खींची गई स्पर्श रेखाएं A पर मिलती है, तो ∠PAQ=48∘,then ∠APQ कितना होगा ?
View Solutionदो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते है । A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित है । सिद्ध कीजिए कि BP=BQ है ।
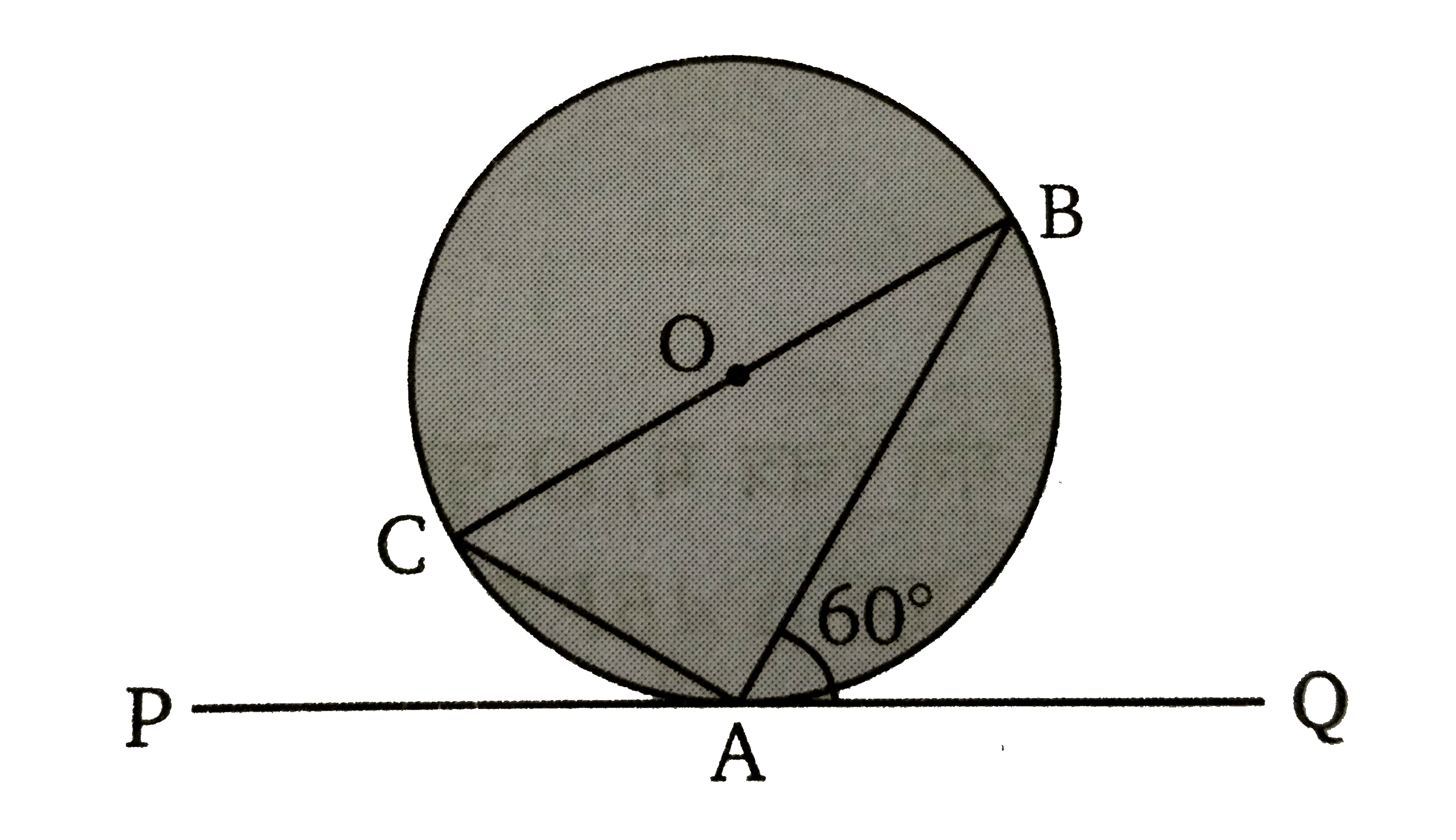
View Solutionदिये गए चित्र में O केन्द्र वाले एक वृत्त के बिन्दु A पर PAQ एक स्पर्शी है तथा ∠BAQ=60∘ तब ∠ABC का मान ज्ञात कीजिए ।
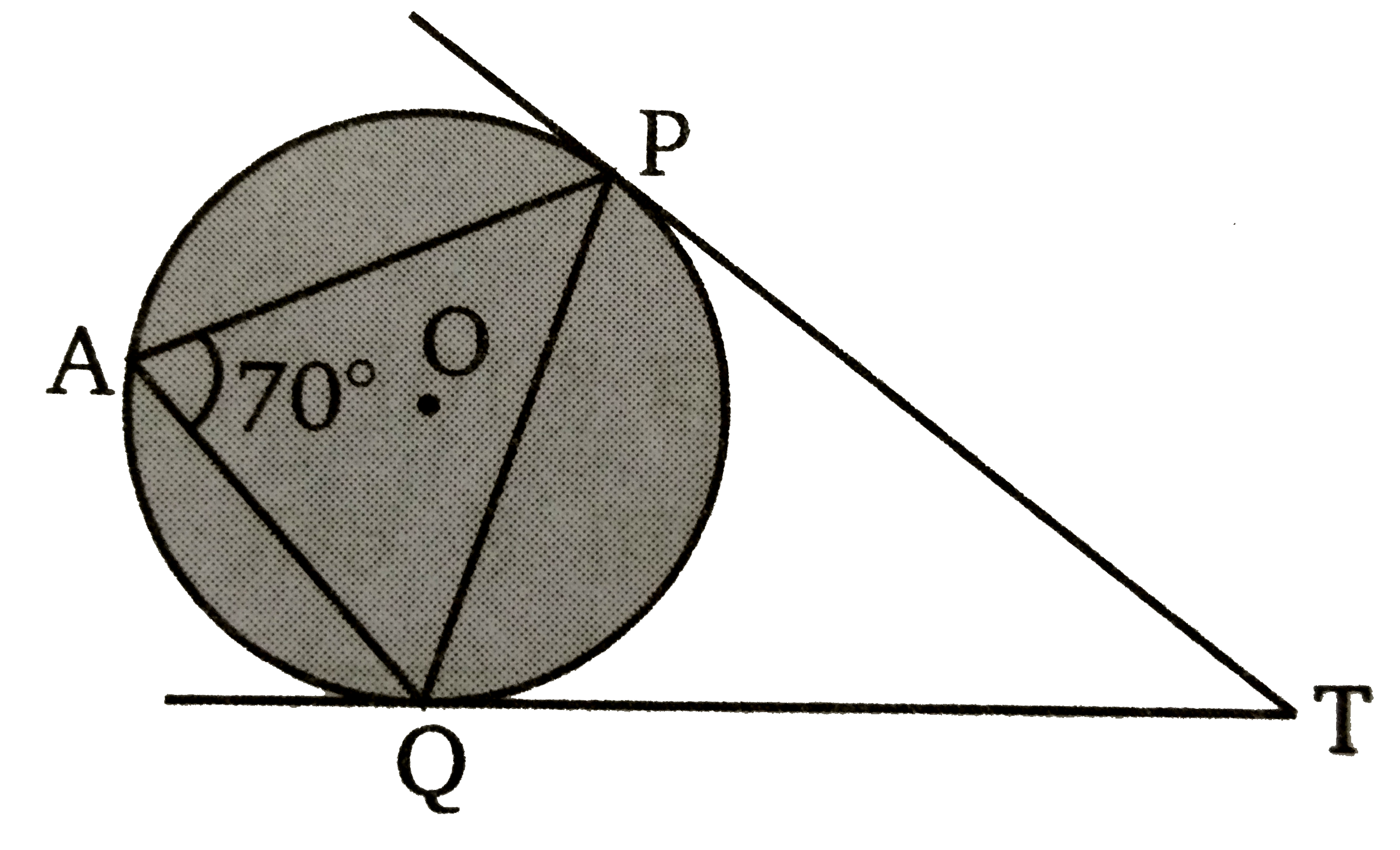
View Solutionदिये गए चित्र में, O वृत्त का केन्द्र है। वृत्त के बाहर एक बिन्दु T से वृत्त पर दो स्पर्शी TP व TQ खींची गयी है। यहाँ स्पर्श जीवा वृत्त के शेष भाग से ∠PAQ=70∘ बनाती है। तब दोनों स्पर्शियाँ के बीच का कोण ज्ञात कीजिए ।
View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat SP=SR.[GP−X]
View SolutionTwo tangents are drawn from an external point A of the circle with centre at O which touches the circle at the points B and C. Prove that AO is the perpendicular bisector of BC.
View SolutionProve that the internal bisector of the angle between two tangents drawn from an external point of a circle will pass through the centre of the circle.
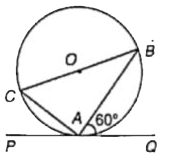
View SolutionIn the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ=60∘, find ∠ABC :
View SolutionProve that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
View Solutionপ্রমাণ করো যে, স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব বৃত্তের কেন্দ্রগামী
View SolutionO কেন্দ্রীয় একটি বৃত্ত এঁকেছি যার একটি ব্যাস AB এবং A বিন্দুতে বৃত্তের স্পর্শক PAQ,PAQ-এর সমান্তরাল জ্যা RS,যুক্তি দিয়ে প্রমাণ করো যে AB, RS-এর লম্বসমদ্বিখন্ডক।
View Solution
