y=−5t2+2t+20
x=2t
A cannonball is shot out of a cannon at a 45∘ angle with an approxiate speed of 283m/s. The cannon from which the ball was fired sits on the edges of a cliff, and its height above the ground is 20 meters. The equations given above represent the cannonball's height above the ground(y) and its horizontal distance (x) from the face of the cliff, t seconds after the ball was fired, where t≥0. How many seconds after the ball was fired does its vertical height above the ground equal its horizontal distance from the cliff?
1
2
3
4
The correct Answer is:B
Difficult: Medium
Category: Passport to Advanced Math/ Quadratics
Strategy Advice: In real-world scenario's a good bit of the text is probably just providing the context of the question. Be sure to focus on what the question is asking (here, find t when x and y are equal).
Getting to the Answer: Because both equations are given in terms of t, set the the equation equal to each other and simplify:
−5t2+2t+20=0
−5t2+20=0
The resulting equation is quadratic, so you can either factor and solve, or use square rooting.
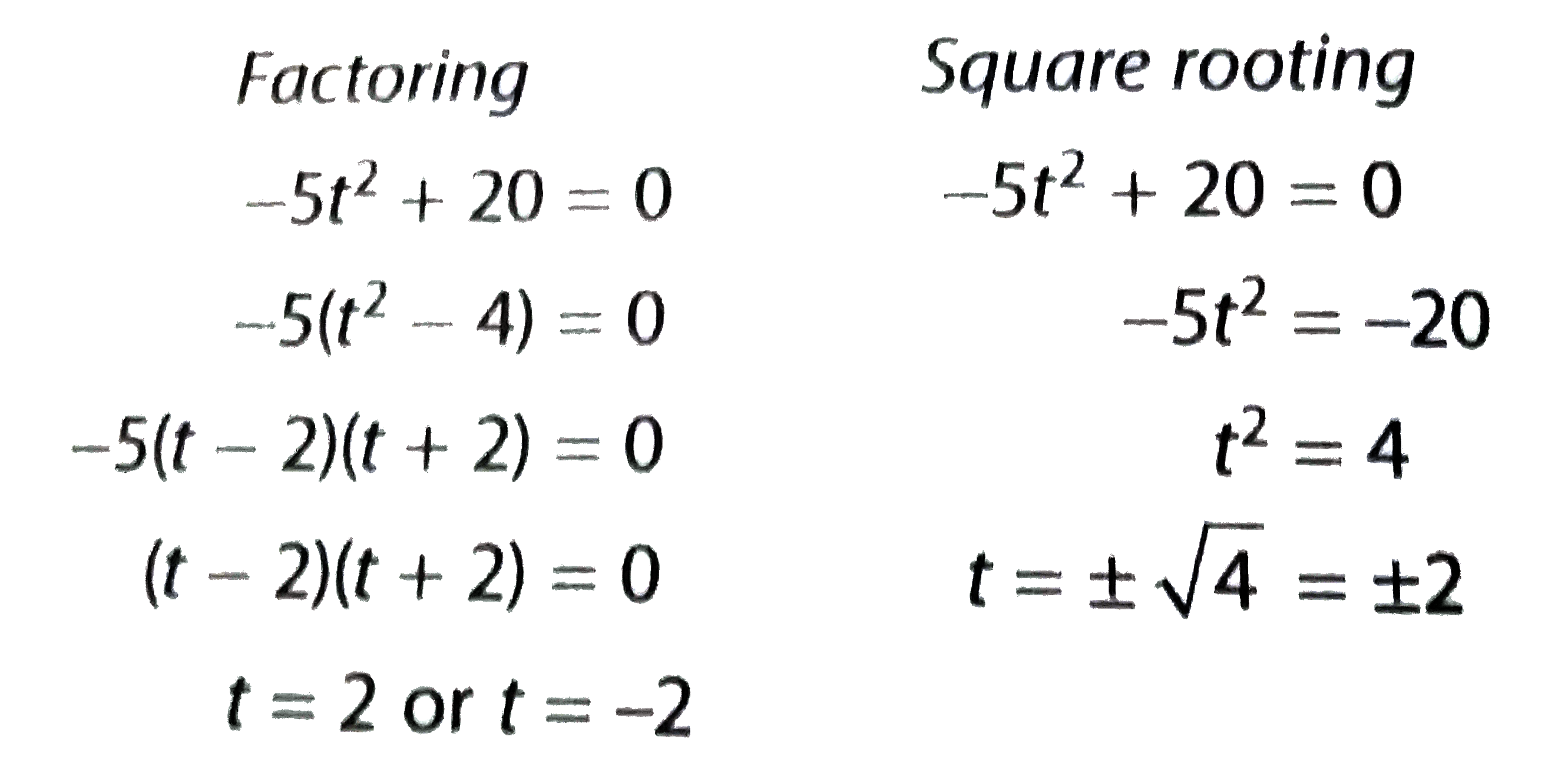
Time can't negative, so t must equal 2. This matches (B).
Topper's Solved these Questions
Similar Questions
Knowledge Check
Joe throws a ball upwards from a certain height above the ground level. The height of the ball above the ground after time t seconds from when the ball was thrown is given by the expression h(t)=−(t−a)2+b. The ball reaches a maximum height of 25 feet after 4 seconds. After how much time [in seconds] will the ball reach the ground level?
A6B7C8D9
Find the time taken for the ball to strike the ground . If a ball is thrown straight upwards with a speed v from a point h meters above the ground .
View SolutionA lamp is 50ft above the ground. A ball is dropped from the same height from a point 30ft away from the light pole. If ball falls a distance s=16t2ft in t second, then how fast is the shadow of the ball moving along the ground 12s later?
View Solutionh(t)=144t−16t2
The function above represents the height, in feet, a ball reaches t seconds after it is tossed in the air from groud level.
a. What is the maximum height of the ball?
b. After how many seconds will the ball hit the ground before rebounding?
View SolutionA ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA ball thrown horizontally with velocity v from the top of a tower of height h reaches the ground in t seconds. If another ball of double the mass is thrown horizontally with velocity 3v from the top of another tower of height 4h it reaches the ground in (seconds). In the above problem if the first ball reaches the ground at a horizontal distance d, the second ball reaches the ground at a horizontal distance
View SolutionA ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find a. the time it takes to reach the ground, b. the horizontal distance it travels before reaching the ground c. the velocity (direction and magnitude) with which it strikes the ground.
View SolutionTwo 20kg cannon balls are chained together and fired horizontally with a velocity of 200m/s from the top of a 30m wall. The chain breaks during the flight of the cannon balls and one of them strikes the ground at t=2s, at a distance of 250m from the foot fo the wall, and 5m to the right of line of fire determine the position of the other cannon ball at that instant Neglect the resistance of air.

View Solution
