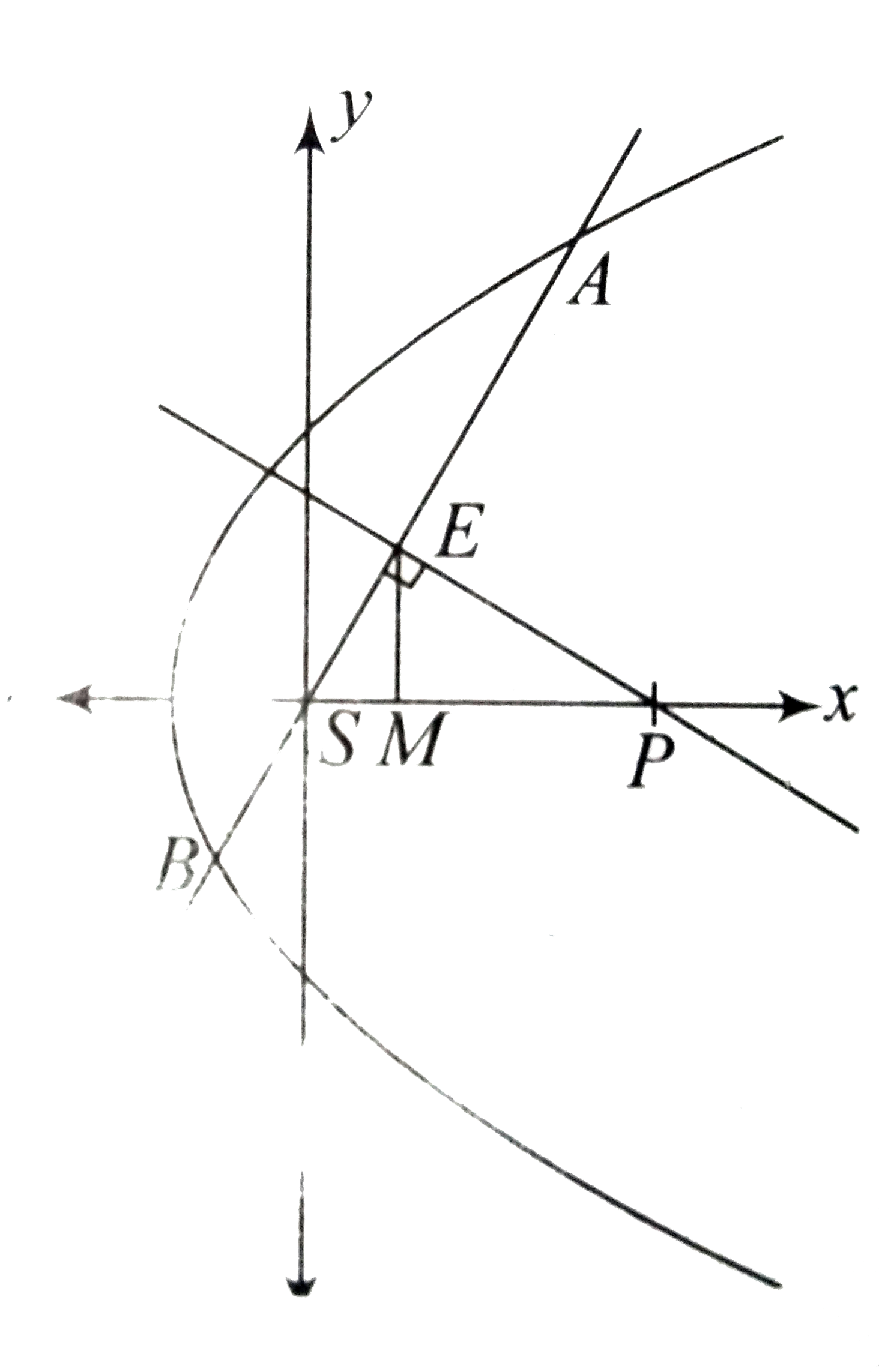
y=√3x+λ is drawn through focus S of the parabola y2=8x+16. If two intersection points of the given line and the parabola are A and B such that perpendicular bisector of AB intersects the x-axis at P then length of PS is
8/7
7/17
8√3
16/3
The correct Answer is:D
y2=8x+16
⇒y2=8(x+2)
Thus, focus is (0,0)
So, line is y=√3x. Solving this line with parabola,
3x2−8x−16=0
i.e., x1+x2=83
⇒x1+x22=43
So, x-coordinate of E is 4/3.
∠PSE=60∘
∴SP=2SE
SE=SMsec60∘=83∴SP=16/3.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type10videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type2videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type18videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
The sraight line 3x−4y+c=0 Intersects the parabola x2=4y at the points A and B. Ifthe tangents to the parabola at A and B are perpendicular, then c =
View SolutionThe locus of the point of intersection of tangents to the parabola y2=4(x+1) and y2=8(x+2) which are perpendicular to each other is
View Solution
Knowledge Check
- Question 1 - Select One
A focal chord for parabola y2=8(x+2) is inclined at an angle of 60∘ with positive x-axis and intersects the parabola at P and Q. Let perpendicular bisector of the chord PQ intersects the x-axis at R, then the distance of R from focus is :
A83B16√33C163D8√3 - Question 2 - Select One
A focal chord for parabola y2=8(x+2) is inclined at an angle of 60∘ with positive x-axis and intersects the parabola at P and Q. Let perpendicular bisector of the chord PQ intersects the x-axis at R, then the distance of R from focus is :
A83B16√33C163D8√3 - Question 3 - Select One
A line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
Amin(−∞,−1)∪(1,∞)Bm∈(−∞,0)∪(0,∞)Cmin(−∞,0)∪(0,∞)Dnone of these
P is a point on the parabola y2=4x and Q is IS a point on the line 2x+y+4=0. If the line x−y+1=0 is the perpendicular bisector of PQ, then the co-ordinates of P can be:
View SolutionA circle is drawn having centre at C(0,2) and passing through focus (S) of the parabola y2=8x, if radius (CS) intersects the parabola at point P, then
View SolutionA tangent is drawn to the parabola y2=8x at P(2, 4) to intersect the x-axis at Q, from which another tangent is drawn to the parabola to touch it at R. If the normal at R intersects the parabola again at S, then the coordinates of S are
View SolutionThe equation of a straight line drawn through the focus of the parabola y2=−4x at an angle of 120∘ to x axis is
View SolutionA line L passing through the focus of the parabola y2=4(x−1), intersects the parabola in two distinct points. If 'm' be the slope of the line 'L' then
View Solution

