y<x+k1
y>2x+k2
Suppose that on a coordinate plane (0, 0) is a solution to the system of inequalities given above. Which of the following conclusions about k1andk2 must be true?
k1<k2
k2<k1
|k1|<|k2|
k1=−k2
The correct Answer is:B
To solve the problem step by step, we need to analyze the given inequalities and determine the conditions for k1 and k2 based on the fact that the point (0, 0) is a solution to the system of inequalities.
Step 1: Write down the inequalities
The inequalities given are:
1. y<x+k1
2. y>2x+k2
Step 2: Substitute the point (0, 0) into the inequalities
Since (0, 0) is a solution, we substitute x=0 and y=0 into both inequalities.
For the first inequality:
0<0+k1
This simplifies to:
0<k1
This means that k1 must be greater than 0.
For the second inequality:
0>2(0)+k2
This simplifies to:
0>k2
This means that k2 must be less than 0.
Step 3: Analyze the relationship between k1 and k2
From the results of the substitutions:
- We found that k1>0
- We found that k2<0
Step 4: Conclude the relationship between k1 and k2
Since k1 is positive and k2 is negative, we can conclude that:
k1>k2
Final Conclusion
The conclusion we can draw from the inequalities is that k1 must be greater than k2.
---
The inequalities given are:
1. y<x+k1
2. y>2x+k2
Since (0, 0) is a solution, we substitute x=0 and y=0 into both inequalities.
0<0+k1
This simplifies to:
0<k1
This means that k1 must be greater than 0.
0>2(0)+k2
This simplifies to:
0>k2
This means that k2 must be less than 0.
From the results of the substitutions:
- We found that k1>0
- We found that k2<0
Since k1 is positive and k2 is negative, we can conclude that:
k1>k2
The conclusion we can draw from the inequalities is that k1 must be greater than k2.
Topper's Solved these Questions
Similar Questions
Find the vlaue of k for which the roots of the following equation are real and equal k2x2−2(2k−1)x+4=0
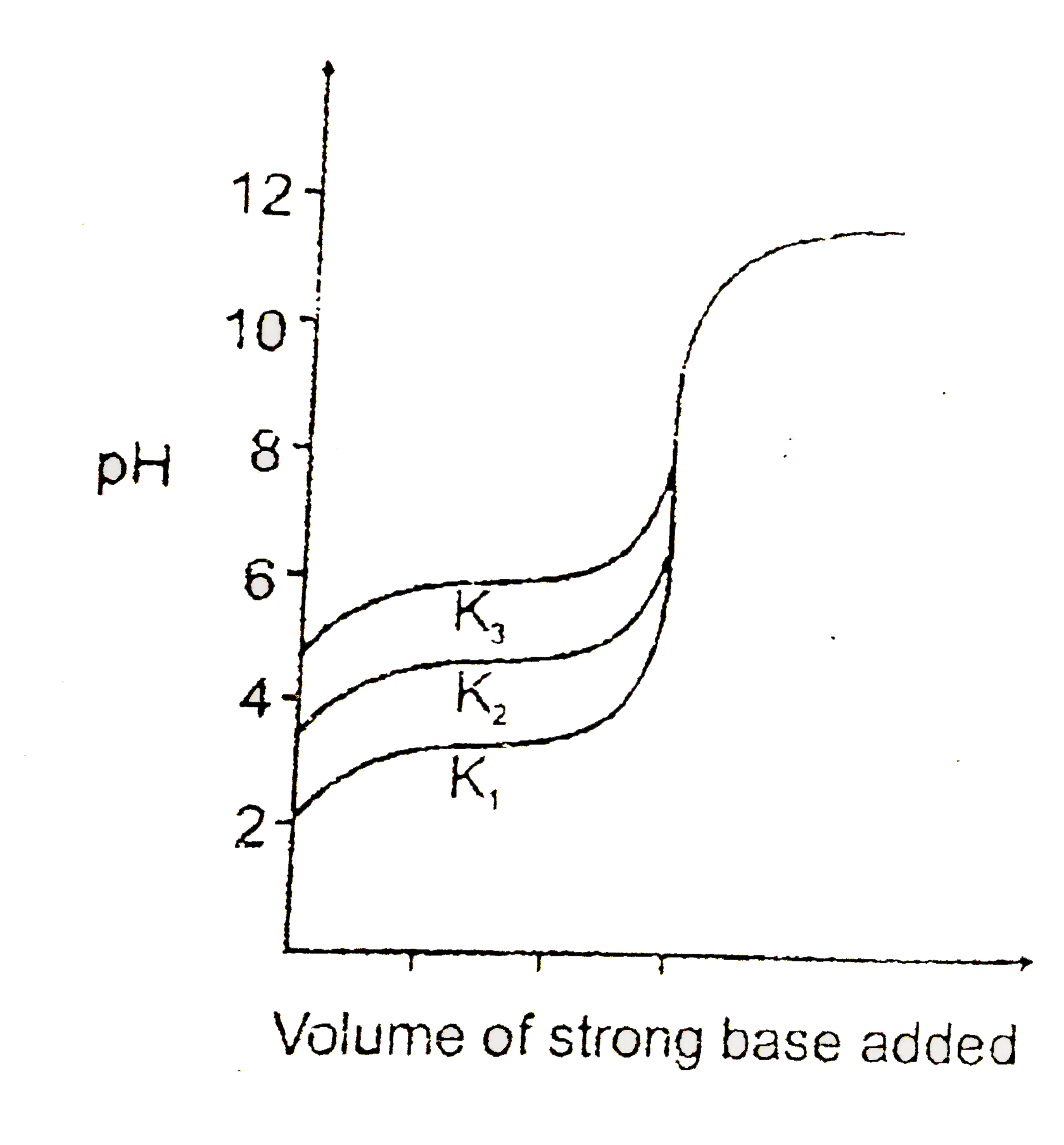
View SolutionTitration curves of 0.1M solution of three weak acids HA1,HA2 and HA3 with ionization constants K1,K2 and K3 respectively with a strong base are plotted as shown in the figure. Which of the following options is//are true?
View Solution
Knowledge Check
If 0<k<1, then which one of the following must be less than k?
A3k/2B1/kC|k|Dk2
Write the value of k for which the system of equations x+y−4=0 and 2x+ky−3=0 has no solution
View SolutionFind the value of k for which the following system of equation has no solution: x+2y=0, 2x+ky=5
View Solution(k−1)x+13y=4
k(x+2y)=7
In the system of linear equations above, k is a constant. If the system has no system, what is the value of k?
View SolutionWrite the value of k for which the system of equations 3x−2y=0 and kx+5y=0 has infinitely many solutions.
View SolutionWrite the values of k for which the system of equations x+ky=0, 2x−y=0 has unique solution.
View SolutionFind the value of k for which following system of equations have infinitely many solution: kx+3y=2k+1, 2(k+1)x+9y=7k+1
View SolutionFind the value of k for which following system of equations have infinitely many solution: 2x−3y=7, (k+2)x−(2k+1)y=3(2k−1)
View Solution
