Complete Solutions to EXERCISE of chapter 2020 QUESTION PAPER (1) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | 2020 QUESTION PAPER (1) |
| AGRAWAL PUBLICATION | EXERCISE |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Two right circular cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1, what is the ratio of their volumes?
View SolutionUsing the empirical formula, find the mode of a distribution whose mean is 8.32 and the median is 8.05.
View SolutionThe probability that it will rain tomorrow is 0.85. What is the probability that it will not rain tomorrow?
View SolutionWhat is the arithmetic mean of the first 'n' natural numbers?
View SolutionFind the `11^(th)` term from the last term of the AP 12, 8, 4,…………..-84.
View SolutionSolve the equation: 1 + 5 + 9 + 13 +…….+x = 1326.
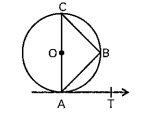
View SolutionIn the figure, AB is a chord with centre O, AOC is the diameter and AT is a tangent touching the circle at A. Prove that `angle BAT` = `angle ACB`.
View SolutionIf `tan theta = 3/4`, find the value of `(1 - cos^2 theta)/(1 + cos^2 theta)`
View SolutionIf `tan theta = sqrt 3`, find the value of `(2 sec theta)/(1 + tan^2 theta)`
View SolutionStudents of Class XII presencted a gift to their school in the from of an electric lamp in the shape of a glass hemispherical base surmounted by a metallic cylindrical top of same radius 21 cm and height 3.5 cm. The top was silver coated and the glass surface was painted red
What is the cost of silver coating the top at the rate of `Rs.5 per 100 cm^2`?
View SolutionStudents of Class XII presencted a gift to their school in the from of an electric lamp in the shape of a glass hemispherical base surmounted by a metallic cylindrical top of same radius 21 cm and height 3.5 cm. The top was silver coated and the glass surface was painted red
What is the surface area of glass to be painted red?
View SolutionFind the probability that a leap year selected at random will contain 53 Sundays and 53 Mondays.
View SolutionFind the value of p, if the mean of the following distribution is 7.5

View SolutionFind a, b and c if its is given that the numbers a, 7, b, 23, c are in an AP.
View SolutionIf m times the `m^(th)` term of an AP is equal to n times its `n^(th)` term, show that the `(m + n)^(th)` term of the AP is zero.
View SolutionFind the value of k, for which the quadratic equation `(k + 4)^2 + (k +1)x+1 = 0` has equal roots.
View SolutionOn dividing `(x^(3)-3x^(2)+x+2)` by a polynomial g(x), the quotient and remainder are (x-2) and (-2x+4) respectively. Find g(x).
View SolutionIf the sum of the squares of zeroes of the quadractic polynomial f(x) = `x^2 - 8x + k` is 40, find the value of k.
View SolutionIn what ratio does the point P(-4,y) divide the line segmetn joining the points A(-6,10) and B(3, -8) if its lies on AB. Also, find the value of y.
View SolutionProve that a tangent to a circle is perpendicular to the radius throught the point of contact.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionIn a right triangle, prove that the squre of the hypotenuse is equal to the sum of squares of the other two sides.
View SolutionIf `sin theta + cos theta` = p and `sec theta + cosec theta` = q. show that `q(p^2 - 1)= 2p`.
View Solution500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of the water level in the pond, if the average displacement of the water by a person is `0.04 m^3`?
View SolutionShow that `(12)^n` cannot end with digit 0 or 5 for any natural number n.
View SolutionProve that `(sqrt 2 + sqrt 5)`is irrational.
View SolutionA train covered a certain distance at a uniform speed. If the train would have been `6 km/hr`. Faster it would have taken 4 hours less than the scheduled time and it the train would have slowed down by `6 km/hr`. It would have taken 6 hours more than the scheduled time. find the length of the journey.
View SolutionIf an equilateral triangle ABCD is a point on the side BC such that BD = `1/3`, prove that `9 AD^2 = 7AB^2`.
View SolutionProve that the sum of squres of the sides of a rhombus is equal to the sum of the squares of its diagonals.
View SolutionIf the angle of elevation of a cloud from a point 10 metres above a lake is s`30^@` and the angle of depression of its reflection in the lake is `60^@`. Find the height of the cloud from the surface lake.
View SolutionA vertical tower of height 20 m stands on a horizontal plane and is surmounted by a vertical flag staff of heigh h. At a point on the plane, the angle of elevation of the bottom and tap of the flaga staff are `45^@` and `60^@` respectively. Find the value of h.
View SolutionA solid iron cuboidal block of dimensions `4.4 m xx 2.6 mxx 1 m` is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. find the length of the pipe.
View SolutionFor the following frequency distribution, draw a cumulatiave frequency curve of more than type and hence obtain the median value.

View Solution
EXERCISE questions and complete solutions for chapter 2020 QUESTION PAPER (1) of AGRAWAL PUBLICATION of Class 10