Complete Solutions to EXERCISE of chapter SAMPLE PAPER 6 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SAMPLE PAPER 6 |
| AGRAWAL PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
`(cot A+tanB)/(cotB+tanA)` is :
View SolutionFor any two positive integers 'a' and b, what is the value of HCF `(a,b),`LCM (a, b)?
View SolutionUsing prime factorisation method, find the HCF and LCM of 210 and 175
View SolutionFind the mean of first 10 odd natural numbers.
View SolutionIf `2x ,x+10 ,3x+2` are in A.P., find the value of `xdot`
View SolutionBy taking `A = 90^@ and B = 30^@` , show that sin (A - B) = sin A cos B-cos A sin B.
View SolutionThe value of `(cos 0^(@) + sin 45^(@) + sin 30^(@)) (sin 90^(@) - cos 45^(@) + cos 60^(@))` is
View SolutionThe degree of the polynomial `(x+1)(x^(2)-x-x^(4)+1)` is:
View SolutionFind the ratio of the volume of a right circular cone to that of the volume of right circular cylinder, of equal diameter and height.
View SolutionWrite a quadratic polynomial sum of whose zeros is 3 and product is -6.
View SolutionThe value of c for which the pair of equations `cx -y=2 and 6x- 2y=3` will have infinitely many solutions is
View SolutionDetermine the probability of getting a number which is neither prime nor composite in single throw of a fair dice.
View SolutionFind the mean of the following data:
1,7,9,3,4,5,6.
View SolutionIf P(E) = 0.001, then find the value of `P(vecE)`.
View SolutionOne card is drawn at random from a well shuffled deck of 52 cards. What is the probability to get a face card ?
View SolutionA die is thrown once. What is the probability of getting a prime number?
View SolutionThe ratio of the length of a rod and its shadow is `1:sqrt(3)` .The angle of elevationn of the sun is :
View SolutionWhat is the sum of the roots of the quadratic equation `x^2 - 2x - 15 = 0` ?
View SolutionForm cubic polynomial in x with the sum, sum of the products of its zeros taken two at a time, and product of its zeros are 8, 0 and 9 respectively.
View SolutionWhat is the value of 'p' for which the quadratic equation `2px^2 + 6x + 5 = 0` has equal roots.
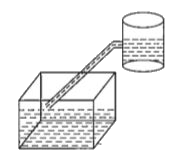
View SolutionSelvi is setting up a water purifier system in her house which includes setting up an overhead tank in the shape of a right circular cylinder. This is filled by pumping water from a sump (underground tank) which is in the shape of a cuboid.
The underground water tank (sump) is a sturdy single moulded piece built to with stand underground pressure and is available in the storage capacity of 2000 L.

These, along with hassle-free installation and minimum maintenance needs make it the ideal water storage solution.
Dimensions (sump): 1.57 m `xx` 1.44 m `xx` 95 cm.
Dimensions (overhead tank):
Radius 60 cm and Height 95 cm
Water flow conditions at the required overload capacity should be checked for critical pressure drop to ensure that valves are adequately sized.
On the basis of the above information, answer the following qeuestions:
The ratio of the capacity of the sump to the capacity of the overhead tank is
View SolutionSelvi is setting up a water purifier system in her house which includes setting up an overhead tank in the shape of a right circular cylinder. This is filled by pumping water from a sump (underground tank) which is in the shape of a cuboid.
The underground water tank (sump) is a sturdy single moulded piece built to with stand underground pressure and is available in the storage capacity of 2000 L.
These, along with hassle-free installation and minimum maintenance needs make it the ideal water storage solution.
Dimensions (sump): 1.57 m `xx` 1.44 m `xx` 95 cm.
Dimensions (overhead tank):
Radius 60 cm and Height 95 cm
Water flow conditions at the required overload capacity should be checked for critical pressure drop to ensure that valves are adequately sized.
On the basis of the above information, answer the following qeuestions:
If overhead tank need to be painted to save it from corrosion, how much area need to be painted?
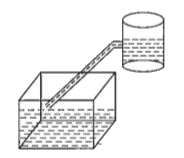
View SolutionSelvi is setting up a water purifier system in her house which includes setting up an overhead tank in the shape of a right circular cylinder. This is filled by pumping water from a sump (underground tank) which is in the shape of a cuboid.
The underground water tank (sump) is a sturdy single moulded piece built to with stand underground pressure and is available in the storage capacity of 2000 L.
These, along with hassle-free installation and minimum maintenance needs make it the ideal water storage solution.
Dimensions (sump): 1.57 m `xx` 1.44 m `xx` 95 cm.
Dimensions (overhead tank):
Radius 60 cm and Height 95 cm
Water flow conditions at the required overload capacity should be checked for critical pressure drop to ensure that valves are adequately sized.
The capacity (in litres) of the overhead tank is
View SolutionSelvi is setting up a water purifier system in her house which includes setting up an overhead tank in the shape of a right circular cylinder. This is filled by pumping water from a sump (underground tank) which is in the shape of a cuboid.
The underground water tank (sump) is a sturdy single moulded piece built to with stand underground pressure and is available in the storage capacity of 2000 L.
These, along with hassle-free installation and minimum maintenance needs make it the ideal water storage solution.
Dimensions (sump): 1.57 m `xx` 1.44 m `xx` 95 cm.
Dimensions (overhead tank):
Radius 60 cm and Height 95 cm
Water flow conditions at the required overload capacity should be checked for critical pressure drop to ensure that valves are adequately sized.
On the basis of the above information, answer the following qeuestions:
If the amount of water in the sump, at an instant, is 1500 litres, then the water level in the sump at that instant is
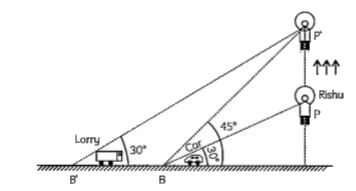
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of `30^@`. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of 45o and a lorry parked at B' at an angle of depression of `30^@`. (Use `sqrt3` = 1.73)
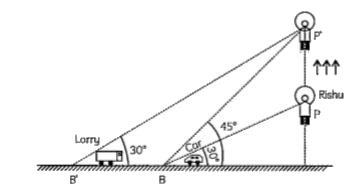
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
If the height of the balloon at point P is 'h' m and distance AB is 'x' m, then 'x' and 'h' are related as:
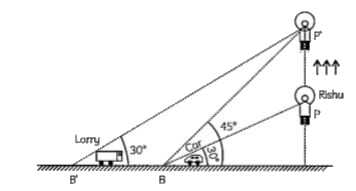
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of `30^@`. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of `45^(@)` and a lorry parked at B' at an angle of depression of `30^@`. (Use `sqrt3` = 1.73)
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
The height of the balloon at point P' and distance AB are related as:
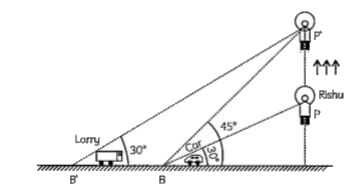
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of `30^@`. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of `45^@` and a lorry parked at B' at an angle of depression of `30^@`. (Use `sqrt3` = 1.73)
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
The height of the balloon at point P, then
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of `30^@`. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of 45o and a lorry parked at B' at an angle of depression of `30^@`. (Use `sqrt3` = 1.73)
The distance AB on the ground is
View SolutionA factory is using an inclined conveyor belt to transport its product from level 1 to 2 which is 3 m above level - 1 as shown in the figure below. The inclined conveyor is supported from one end to level 1 and from the other end to a post located 8 m away from level 1 supporting point.

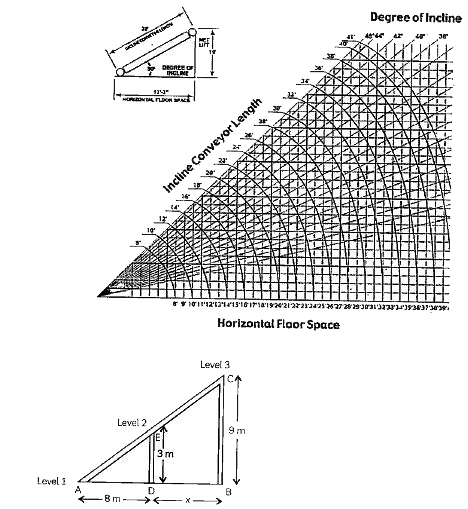
The factory wants to extend the conveyor belt to reach at a new level 3 which is 9 m above level 1 while maintaining the inclination angle.
Which concept of geometry helps in determining the distance at which level 3 should be placed?
View SolutionA factory is using an inclined conveyor belt to transport its product from level 1 to 2 which is 3 m above level - 1 as shown in the figure below. The inclined conveyor is supported from one end to level 1 and from the other end to a post located 8 m away from level 1 supporting point.

The factory wants to extend the conveyor belt to reach at a new level 3 which is 9 m above level 1 while maintaining the inclination angle.
The distance at which a new post is to be installed to support the conveyor belt at level 3, is
View SolutionA factory is using an inclined conveyor belt to transport its product from level 1 to 2 which is 3 m above level - 1 as shown in the figure below. The inclined conveyor is supported from one end to level 1 and from the other end to a post located 8 m away from level 1 supporting point.

The factory wants to extend the conveyor belt to reach at a new level 3 which is 9 m above level 1 while maintaining the inclination angle.
How much distance is extended from D to B?
View SolutionA factory is using an inclined conveyor belt to transport its product from level 1 to 2 which is 3 m above level - 1 as shown in the figure below The inclined conveyor is supported from one end to level 1 and from the other end to a post located 8 m away from level 1 supporting point.

The factory wants to extend the conveyor belt to reach at a new level 3 which is 9 m above level 1 while maintaining the inclination angle.
The length of the conveyor belt up to level 3 is
View SolutionA factory is using an inclined conveyor belt to transport its product from level 1 to 2 which is 3 m above level - 1 as shown in the figure below The inclined conveyor is supported from one end to level 1 and from the other end to a post located 8 m away from level 1 supporting point.

The factory wants to extend the conveyor belt to reach at a new level 3 which is 9 m above level 1 while maintaining the inclination angle.
The length of the conveyor belt up to level 2 is
View SolutionIn order to conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flowerpots have been placed at a distance of 1 m from each other along AD, as shown in given figure below. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th distance AD on the eighth line and posts a red flag.
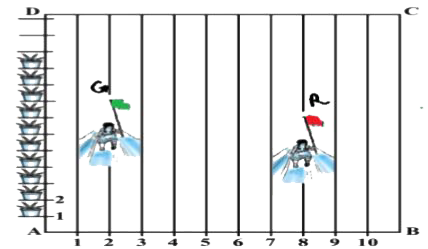
Find the position of green flag
View SolutionIn order to conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flowerpots have been placed at a distance of 1 m from each other along AD, as shown in given figure below. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th distance AD on the eighth line and posts a red flag.
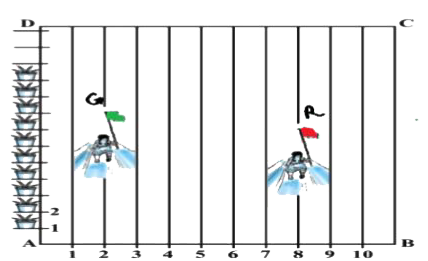
Find the position of red flag
View SolutionIn order to conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flowerpots have been placed at a distance of 1 m from each other along AD, as shown in given figure below. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th distance AD on the eighth line and posts a red flag.
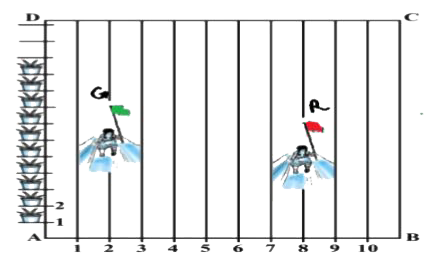
What is the distance between both the flags?
View SolutionDetermine the AP whose 3rd term is 5 and the `7^(th)` term is 9 .
View SolutionThe zeroes of `3x^(2)-4-x` are :
View SolutionFind the coordinates of the point which divides the line Joining (1,-2) and (4,7) internally in the ratio 1:2.
View SolutionFind the third vertex of a triangle, if two of its vertices are at `(-3, 1)` and `(0, -2)` and the centroid is at the origin.
View SolutionTwo dice are thrown simultaneously and the outcomes are noted. Find the probability that:
sum of numbers on the two dice is 5.
View SolutionIf 0.3528 is expressed in the form of `p/(2^m 5^n)` find the simallest values of m, n and p.
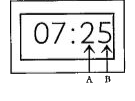
View SolutionAmrish wakes up in the morning and notices that his digital cock recde 07: 25 am. After noon, he looks at the clock again.
What is the probability that
the number in column A is 4 ?
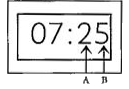
View SolutionAmrish wakes up in the morning and notices that his digital cock recde 07: 25 am. After noon, he looks at the clock again.
What is the probability that
the number in column B is 8 ?
View SolutionThe persons start walking together and their steps measure 40 cm, 42 cm and 45 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
View SolutionThere is a circular park of radius 24 m and there is a pole at a distance of 26 m from the centre of the park os shown in the figure. It is planned to enclose the park by planting trees along line segments PO and PR tangential to the park.
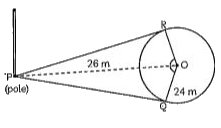
Find the length of PQ and PR.
View Solution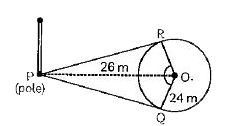
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.
View SolutionThe perpendicular from A on side BC of a `Delta`ABC meets BC at D such that DB = 3CD. Prove that `2AB^2 = 2AC^2 + BC^2`
View SolutionDraw a line segment of length 8 cm and divide it internally in the ratio 4:5.
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.

View SolutionThe mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies `f_1` and `f_2`:
View SolutionSolve for x and y :
`7x - 4y = 49, 5x - 6y=57`
View SolutionThe sum of the reciprocals of Meena's ages (in years) 3 years ago and 5 year hence is `(1)/(3).` Find her present age.
View SolutionA natural number when increased by 12, equals 160 times its reciprocal. Find number.
View SolutionA number consists of two digits. When it id divided by the sum of its digits, the quotient is 6 with no remainder. When the number is diminished by 9, the digits are reversed. Find the number.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are `60o`and `30o`, respectively. Find the hei
View SolutionProve that: `(tantheta/(1-tantheta))-(cottheta/(1-cottheta))=(costheta+sintheta)/(costheta-sintheta)`
View SolutionState and prove Basic Proportionality Theoram (Thales Theoram)
View SolutionWrite the denominator of the rational number ` ( 771)/( 3000)`in the form ` 2 ^(p) 5 ^(q)` , where p and q are non - negative integers
View SolutionIf two positive integers m and n are expressible as as ` m = ab^(2) and n = a^(3) b`, where a and b are prime numbers, then find LCM (m, n)
View SolutionFind the value of the remainder, when ` x^(2) + (a + b) x + ab ` is divided by (x + a)
View SolutionIf the sum of a positive number and its square is 240 , then find the number
View SolutionIf x, x - 2 and 3x are in AP, then find the value of x
View SolutionDetermine the ` 12^(th)` term of the AP, 5, 8, 11, 14, . . . . . .
View SolutionThe sum and the product of the roots of the quadratic equations ` 2 x^(2) + 14 x + 24 = 0 `
View SolutionFind the ratio in which x-axis divides the join of (2,-3) and (5,6).
View SolutionThe distance between the points `(a cos theta+bsin theta, 0)` and `(0, a sin theta - bcos theta)`.
View SolutionPlotting the points A ( - 4, 6) and B ( - 4, -6) on the coordinate axes check if P ( - 4, 2) lies on the line segment AB
View SolutionCheck if the three sides of lengths 3 cm 6 cm and 8 cm can form a right triangle
View SolutionFind the length of a altitude in on equilateral triangle of side 'a' cm
View SolutionState and prove the Pythagoras theorem.
View SolutionFrom the external point P tangents PA and PB are drawn to a circle with centre O. If `angle PAB = 50^(@)`, then find `angle AOB`.
View SolutionSimplify ` (1 + tan ^(2) theta ) ( 1 + sin theta ) ( 1 - sin theta )`
View SolutionIf ` 3 sec theta = 5`, then find the value of ` cot theta `
View SolutionThe total surface area of a cylinder of base radius r and height h is______.
View SolutionIf the area of a circle is `154cm^(2)`, then find its circumference.
View SolutionTwo unbiased coins are tossed simultaneously, then the probability then the probability of getting no head is ` (p)/(q)` . Find the value of ` (p+ q)^(2)`
View SolutionA playgroup school is looking to refurnish the playground area that is in almost a triangular shape (ABC) .There is a small tree ,almost a vertical line in shape lets say AD, at the corner of the playground area
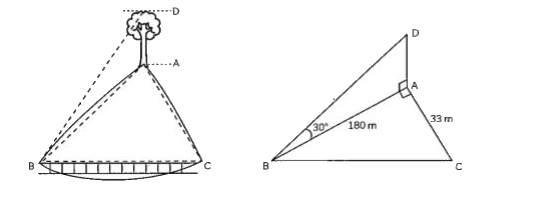
A path runs along the edge BC of the field .As part of material purchase planning ,the playgroup manager needs to scope out the surrounding area including the dimensions of the tree.
The height of the tree AD is :
View SolutionA playgroup school is looking to refurnish the playground area that is in almost a triangular shape (ABC) .There is a small tree ,almost a vertical line in shape lets say AD, at the corner of the playground area
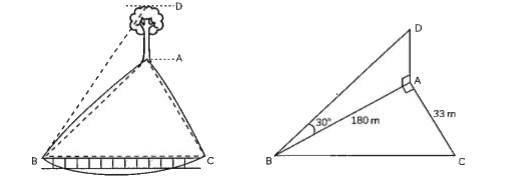
A path runs along the edge BC of the field .As part of material purchase planning ,the playgroup manager needs to scope out the surrounding area including the dimensions of the tree.
On the basis of the above information , answer any four of the following questions :
The length of the path BC is :
View SolutionA playgroup school is looking to refurnish the playground area that is in almost a triangular shape (ABC) .There is a small tree ,almost a vertical line in shape lets say AD, at the corner of the playground area
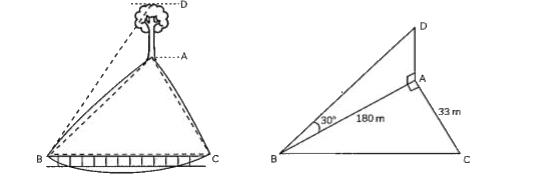
A path runs along the edge BC of the field .As part of material purchase planning ,the playgroup manager needs to scope out the surrounding area including the dimensions of the tree.
On the basis of the above information , answer any four of the following questions :
The area (in sq m) of the field ABC is :
View SolutionA playgroup school is looking to refurnish the playground area that is in almost a triangular shape (ABC) .There is a small tree ,almost a vertical line in shape lets say AD, at the corner of the playground area
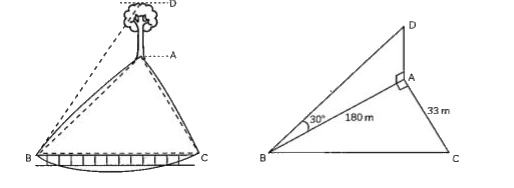
A path runs along the edge BC of the field .As part of material purchase planning ,the playgroup manager needs to scope out the surrounding area including the dimensions of the tree.
The length BD is :
View SolutionIn CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions .
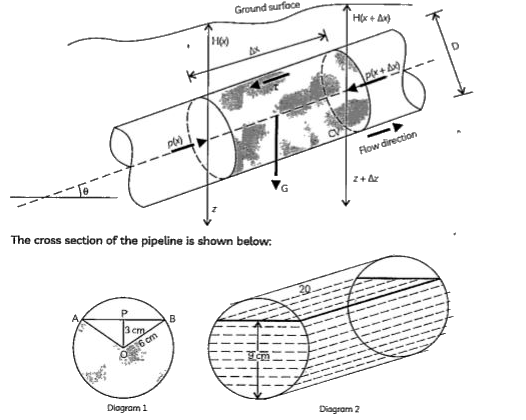
In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm.
The measure of `angleAOB` is :
View SolutionIn CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions .
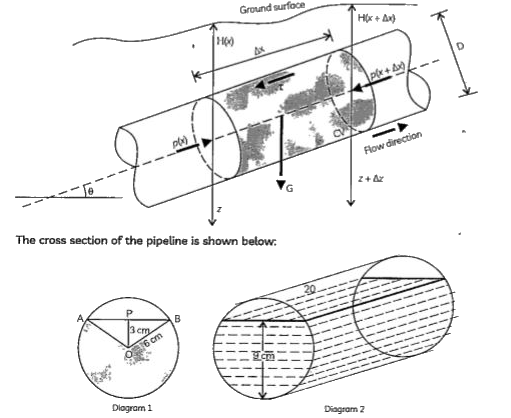
In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm.
The area (in sq cm ) of `DeltaAOB` is :
View SolutionResident Welfare Association (RWA) of a M2 K Society in Azadpur have put up three electric poles A,B and C in a society 's common park near Tower A . Despite these poles ,some parts of the park are still in dark. So , RWA decides to have one more electron pole D in the park.

The position of the pole C is :
View SolutionResident Welfare Association (RWA) of a M2 K Society in Azadpur have put up three electric poles A,B and C in a society 's common park near Tower A . Despite these poles ,some parts of the park are still in dark. So , RWA decides to have one more electron pole D in the park.

The distance of the pole B from the corner O of the park is :
View SolutionResident Welfare Association (RWA) of a M2 K Society in Azadpur have put up three electric poles A,B and C in a society 's common park near Tower A . Despite these poles ,some parts of the park are still in dark. So , RWA decides to have one more electron pole D in the park.

The position of the fourth pole D so that four points A,B,C and D form a parallelogram is :
View SolutionResident Welfare Association (RWA) of a M2 K Society in Azadpur have put up three electric poles A,B and C in a society 's common park near Tower A . Despite these poles ,some parts of the park are still in dark. So , RWA decides to have one more electron pole D in the park.

On the basis of the above information ,answer any four of the following questions :
The distance between poles A and C is :
View SolutionResident Welfare Association (RWA) of a M2 K Society in Azadpur have put up three electric poles A,B and C in a society 's common park near Tower A . Despite these poles ,some parts of the park are still in dark. So , RWA decides to have one more electron pole D in the park.

Plot a point D so that ABCD becomes parallelogram .The distance between poles B and D is :
View SolutionFind the greatest positive integer that will divide 434 and 539 leaving remainders 9 and 12 respectively .
View SolutionFor any positive real number `x` , prove that there exists an irrational number `y` such that `0
View SolutionIf the zeroes of the polynomial `x^3-3x^2+x+1` are `a"\ ""\ "b ,"\ "a ,"\ "a"\ "+"\ "b` , find a and b.
View SolutionThe nth terms of an A.P.`(1)/(m),(m+1)/(m),(2m+1)/(m),...` is:
View SolutionIf `x=rsinAcosC ,\ \ y=rsinAsinC` and `z=rcosA` , prove that `r^2=x^2+y^2+z^2`
View Solution`(tan^2 theta)/((sec theta-1)^2)=(1+cos theta)/(1-cos theta)`
View SolutionThe diameter of a cycle wheel is 21 cm. How many revolutions will it make in moving 66 m ?
View SolutionWithout actually performing the long divison, find if `(987)/(10500)` will have terminating or non-terminating (repeating) decimal expansion. Give reasons for your answer
View SolutionShow that the sum of an A.P. whose first term is a, the second term is b and the last term is c, is equal to `((a+c)(b+c−2a))/(2(b−a))
View SolutionA person on tour has Rs. 4200 for his expenses. If he expenses. If he extends his tour for 3 days, he has to cut down his daily expenses by Rs. 70. Find the original duration of the tour.
View SolutionTheorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
View SolutionSixteen glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 20 cm `xx` 10 cm `xx` 10 cm and then the box is filled with water. Find the volume of water filled in the box.
View Solution
EXERCISE questions and complete solutions for chapter SAMPLE PAPER 6 of AGRAWAL PUBLICATION of Class 10