Complete Solutions to EXERCISE of chapter SAMPLE PAPER 10 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SAMPLE PAPER 10 |
| AGRAWAL PUBLICATION | EXERCISE |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
What is the HCF of the smallest prime number and the smallest composite number?
View SolutionWrite a quadratic equation, sum of whose roots is `-3 sqrt(2)` and their product is 4.
View SolutionIn an A.P. if `S_(n) = 5n^(2) -3n` find the A.P.
OR
From the adjoining figure of a rectangle, find the values of x ond y.

View SolutionFind a point which divides the join of A (-3, 4) and B (9,6) internally in the ratio 3: 2.
View SolutionIf the distance between the points P(2, - 3) and Q (10, y) is 10 units, then find the value of 'y'.
View SolutionDraw a line segment of length 7 cm and divide it in the ratio 2:3.
View SolutionWhat number should be added to the polynomial, `x^(2)+7x-35`, so that 3 is the zero of the polynomial?
View SolutionFor what value of k, do the equations `3x - y + 8 = 0` and `6x - ky = -16` represent coincident lines ?
View SolutionThe 4th term from the end of an AP -11, -8, -5, …, 49 is
View SolutionIf the curved surface ared of a sphere is `4 pi` sq m. then find the diameter of the sphere.
View SolutionWhat is surface area of the resultant cuboid, obtained on joining 2 identical cubes each of edge 2 cm?
View SolutionIf `Delta`ABC is right angled at C, then find the value of cos (A + B)
View SolutionA letter is drawn at random from the letters of the word ERROR. What is probability that the drawn latter is R ?
View SolutionIf cos (A+B) =0 and sin (A-B) = `(sqrt(3))/(2)` then calculate the value of A.
View SolutionIn triangle ABC, right-angled at B. if `tan A = 1/sqrt(3)`,find the value of:`sin A cos C+cos A sin C`
View SolutionIf a fair dice is thrown once, find the probability of getting a number which is even as well as prime.
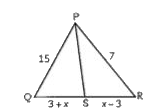
View SolutionIn the given figure, PS is the bisector of `angleQPR` . If PO = 15, PR = 7, QS = 3 + x and SR = x - 3, find the value of x.
View SolutionIf in two triangles ABC and PQR, `(AB)/(PQ) = (BC)/(RP)`, then for the two triangles to be similar, which of the following condition is necessary?
View SolutionIf `6^(th)` term and `8^(th)` term of an A.P. are 12 and 22 respectively, then find its `2^(nd)` term.
View SolutionDetermine zeros of polynomial p(x) `= x^(3) -7x ` .
View SolutionUttar Bantra Sarbojanin Durgotsav Committee had started planning for their Durga puja a year in advance with a mega budget in mind.
Bholeram Tents is given a contract by the municipal corporation of Budaun (Uttar Pradesh), India to setup a mega function pandal (tent). The architect has designed a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m and height 4.4 m surmounted by a right circular cone. This tent is setup in a rectangular park of dimensions 70 m `xx` 60 m as shown below.
The tent is made of canvas. (Take `pi=3.14`)
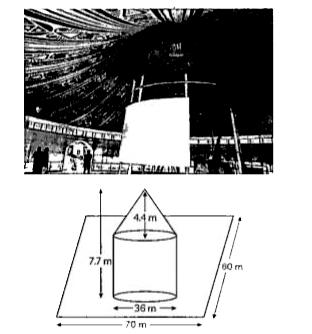
For the workers to finalise the purchase of material, the height of the conical part is:
View SolutionUttar Bantra Sarbojanin Durgotsav Committee had started planning for their Durga puja a year in advance with a mega budget in mind.
Bholeram Tents is given a contract by the municipal corporation of Budaun (Uttar Pradesh), India to setup a mega function pandal (tent). The architect has designed a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m and height 4.4 m surmounted by a right circular cone. This tent is setup in a rectangular park of dimensions 70 m `xx` 60 m as shown below.
The tent is made of canvas. (Take `pi=3.14`)
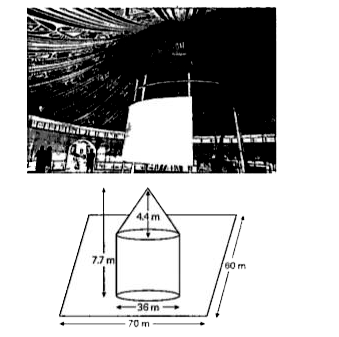
The slant height of the conical part is:
View SolutionUttar Bantra Sarbojanin Durgotsav Committee had started planning for their Durga puja a year in advance with a mega budget in mind.
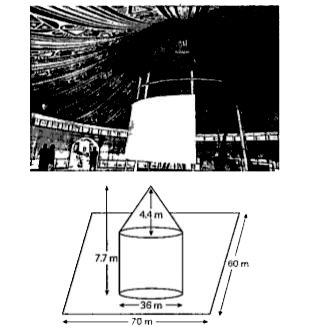
Bholeram Tents is given a contract by the municipal corporation of Budaun (Uttar Pradesh), India to setup a mega function pandal (tent). The architect has designed a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m and height 4.4 m surmounted by a right circular cone. This tent is setup in a rectangular park of dimensions 70 m `xx` 60 m as shown below.
The tent is made of canvas. (Take `pi=3.14`)

To purchase the canvas, the area of the canvas to be used approx in making the tent, is:
View SolutionUttar Bantra Sarbojanin Durgotsav Committee had started planning for their Durga puja a year in advance with a mega budget in mind.
Bholeram Tents is given a contract by the municipal corporation of Budaun (Uttar Pradesh), India to setup a mega function pandal (tent). The architect has designed a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m and height 4.4 m surmounted by a right circular cone. This tent is setup in a rectangular park of dimensions 70 m `xx` 60 m as shown below.
The tent is made of canvas. (Take `pi=3.14`)
The cost of canvas at ₹ 4.50, sq m is:
View SolutionUttar Bantra Sarbojanin Durgotsav Committee had started planning for their Durga puja a year in advance with a mega budget in mind.
Bholeram Tents is given a contract by the municipal corporation of Budaun (Uttar Pradesh), India to setup a mega function pandal (tent). The architect has designed a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m and height 4.4 m surmounted by a right circular cone. This tent is setup in a rectangular park of dimensions 70 m `xx` 60 m as shown below.
The tent is made of canvas. (Take `pi=3.14`)
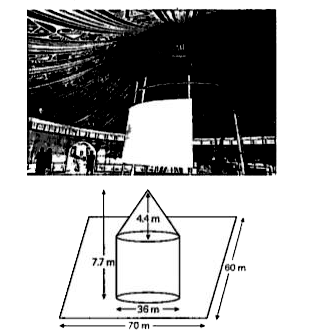
The area of the rectangular park outside the tent is:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
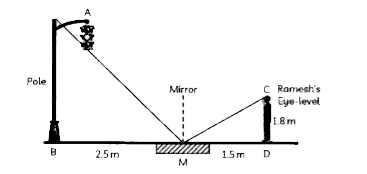
The two similar triangles shown in the figure are:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

Which criterion of similarity is applicable to similar triangles?
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
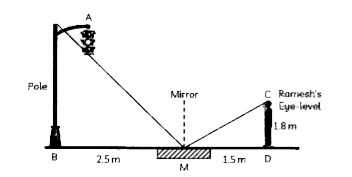
The height of the pole is:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
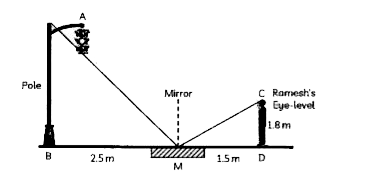
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:
View Solution4 boys are having a night in and one of the boy's mother decides to play a game. 17 cards numbered 1, 2, 3_17 are put in a box and mixed thoroughly.
The mother asks each boy to draw a card and after each draw, the card is replaced back in the box. She shows some magic tricks and at the end, decides to test their mathematical skills.

The probability of drawing an odd number card in the first draw by the first boy is:
View Solution4 boys are having a night in and one of the boy's mother decides to play a game. 17 cards numbered 1, 2, 3 . 17 are put in a box and mixed thoroughly. The mother asks each boy to draw a card and after each draw, the card is replaced back in the.box. She shows some magic tricks and at the end, decides to test their mathematical skills.

The probability of drawing a prime number card in the second draw by the second boy is
View Solution4 boys are having a night in and one of the boy's mother decides to play a game. 17 cards numbered 1, 2, 3_17 are put in a box and mixed thoroughly.
The mother asks each boy to draw a card and after each draw, the card is replaced back in the box. She shows some magic tricks and at the end, decides to test their mathematical skills.

If the card is not replaced after the second draw, the probability of drawing a card bearing a multiple of 3 greater than 4 in the third draw by the third boy is:
View SolutionUsing prime factorisation, find the LCM of 90 and 120.
View SolutionUsing the quadratic formula, find the roots of the quadratic equation: `x^(2) + x - 12 = 0.`
View SolutionIf tan A `= (7)/(24)` find the value of sin A cos A.
View SolutionProve that `sin^(2) A+ sin^(2) A tan^(2) A = tan^(2) A . `
View SolutionIf the centroid of `Delta ABC` having vertices A(a, b), B(b, c) and C(c, a) is the origin, then find the value of (a+b+c).
View SolutionThe perimeter of a sheet of paper in the shape of a quadrant of a circle is 75 cm. Find its area
View SolutionIf `sin theta + cos theta = sqrt 3`, then what is `tan theta + cot theta` equal to ?
View SolutionEvaluate : `(sin 30^(@) + tan45^(@) - cosec 60^(@))/(sec 30^(@) + cos 60^(@) + cot 45^(@))`
View SolutionIf the points `A(1,-2),B(2,3),C(a,2)andD(-4,-3)` forms a parallelogram, find the value of 'a'.
View SolutionIn the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
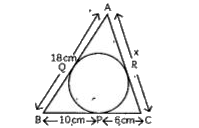
View SolutionThe product of the LCM and HCF of two numbers is 24.The difference of the two numbers is 2.Find the numbers?
View SolutionHow many spherical lead shots each 4.2 cm in diameter can be obtained from a rectangular solid of lead with dimensions 66cm, 42cm, 21cm. `(u s epi=(22)/7)dot`
View SolutionThe first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
View SolutionA tree is broken by the wind. The top of that tree struck the ground at an angle of` 30^(@)` and at a distance of 30 m from the root. Find the height of the whole tree. ( `sqrt(3)` = 1.73)
View SolutionTheorem 6.8 : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionWrite any two irrational numbers whose product is rational number.
View SolutionLCM of `( 2^(3) xx 3 xx5) and ( 2^(4) xx 5xx 7) ` is
View SolutionA quadratic polynomial , whose zeroes are `-3` and 4 is
View SolutionDiscuss the nature of the quadratic equation `2x^(2)+x+4=0`
View SolutionWrite the 2nd term of the AP, if its `S_(n)=n^(2)+2n`.
View SolutionFind the roots of `x+(1)/(x)=2`
View SolutionWrite a pair of linear equations which has the unique solution `x=-1,y=3`
View SolutionIf the distance between the points (4,p) and (1,0) is 5 , then find the value of p.
View SolutionFind the distance between the points (0, 6) and (0, -2).
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
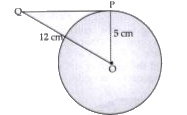
View SolutionState and prove the Pythagoras theorem.
View SolutionFrom a tank containing 10 male fish and 12 female fish, a fish is taken out, then probability that it is a female fish is?
View SolutionFind the number if eight times of its is added to its square, the sum so obtained is -16.
View SolutionFind the value of `(1+cos A)(1-cos A)cosec^(2)A`.
View SolutionFind the maximum value of `(1)/(cosectheta)`
View SolutionIf tan `theta + cot theta = 2` then the value of `tan^2 theta + cot^2 theta` is
View SolutionCase Study-1:
Due to covid-19 lockdown, Ramesh decides to redo his house garden with some plantation work with his son. They have an equilateral triangle shaped garden and he has planted the garden with 6 different types of flowers (each of radius 1 m within a circular area). This left the remaining part of garden (that is outside the circular plants area) with lush green grass.
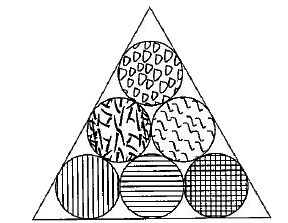
Now, comes the part of adding boundaries to corner the garden off nicely and he needs to know some calculations for it.
A boundary wall of height 25 cm is to be made around the garden leaving a space of 1 m wide for a gate on one side. The total length of boundary wall is
View SolutionThe students of a shool decided to beautifly the school on the annual day by fixing colourful flags on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 m. The flags are stored at the position of the middle most flag. Ruchi was given the responsibility of placing the flags.
Ruchi kept her books where the flags wer stored. She could carry only one flag at a time. How much distance she did cover in completing this job and returning back to collect her books ? What is the maximum distance she travelled carrying a flag ?
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by `h=-16t^(2)+64t+80`
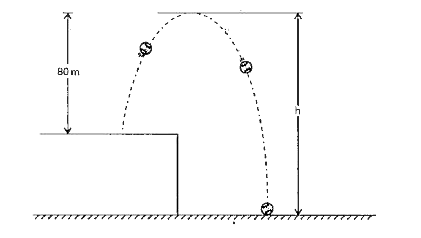
What is the height reached by the ball after 1 second ?
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by `h=-16t^(2)+64t+80`

What is the maximum height reached by the ball ?
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by `h=-16t^(2)+64t+80`
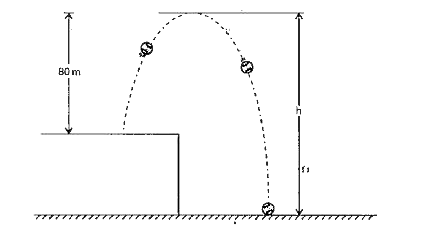
How long will the ball take to hit the ground ?
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by `h=-16t^(2)+64t+80`
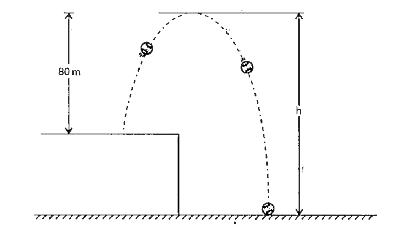
What are the two possible times to reach the ball at the same height of 128 m ?
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by `h=-16t^(2)+64t+80`

After 6 seconds, where is the ball ?
View SolutionAssuming that `sqrt(2)` is irrational, show that `5+sqrt(2)` is an irrational number.
View SolutionFind the greatest number that divides 338 and 59 and leaves remainders of 2 and 5 respectively.
View SolutionThree consecutive vertices of a parallelogram are (-2,-1), (1,0) and (4,3). Find the fourth vertex
View SolutionThe perpendicular bisector of the line segment joining the points A(1,5) and B(4,6) cuts the Y-axis at
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionFind the angle of elevation of the sun when the shadow of a pole 'h' metres high is `sqrt3h` metres long.
View SolutionThe ratio of the volume of a cube to that of a sphere which will fit inside the cube is
View SolutionThe volume of the largest right circular cone that can be cut out of a cube of edge 7 cm ?
(Use `pi = (22)/(7)`)
View SolutionDetermine the zeroes of the polynomial `p(x)=x^(3)-2x^(2)`. Also verify the relationship between the zeroes and the coefficient.
View Solution₹ 250 were divided equally among a certain number of children. If there were 25 more children, each would have received 50 paise less. Find the number of children.
View SolutionIf the centre of a circle is (2a,a-7) ,then Find the value of a , if the ciecle passes through the point (11,-9) and has diameter `10sqrt(2)` units .
View SolutionIn the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
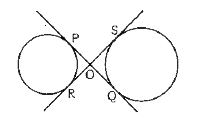
View SolutionIn `DeltaABC, angleA` is acute. BD and CE are perpendicular on AC and AB respectively. Prove that `ABxxAE=ACxxAD`.
View SolutionDraw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is `60^(@)`. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
View SolutionIf `x=acos^(3)theta and y = bsin^(3)theta`, prove that `((x)/(a))^(2//3)+((y)/(b))^(2//3)=1.`
View SolutionI toss three coins together. The possible outocmes are no heads, 1 head 2 head and 3 heads. So, I say that prbability of no heads is `(1)/(4)`. What is wrong with this conclusion?
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View SolutionProve that `(1+sec A-tan A)/(1+sec A+tan A)=1-sin A/(cos A)`
View Solution
EXERCISE questions and complete solutions for chapter SAMPLE PAPER 10 of AGRAWAL PUBLICATION of Class 10