In the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
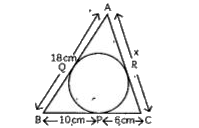
Step by step video & image solution for In the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure, sides of △ABC are tangents to the circle touching the circle at points P, Q abd R as shown. If AQ=3 cm, BR=7 cm and PC= 4 c m, then perimeter of △ABC is

View SolutionIn the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ
(ii) Area (△ABC)=12(Perimeter of△ABC)×r

View Solution
Knowledge Check
In figure , the sides AB, BC and CA of triangle ABC, touch a circle at P,Q and R, respectively . If PA = 4 cm , BP = 3 cm and AC = 11 cm , then length of BC is
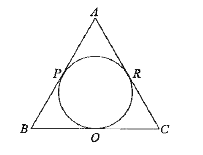 A11 cmB15 cmC14 cmD10 cm
A11 cmB15 cmC14 cmD10 cmIn the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
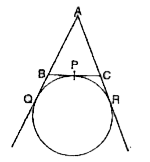 AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABCΔABC is an isosceles triangle and AB = AC. If all the sides AB. BC and CA of a ΔABC touch a circle at D, E and F respectively. Then BE is equal to :
A12 BCB13 BCC14 BCD23 BC
A circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
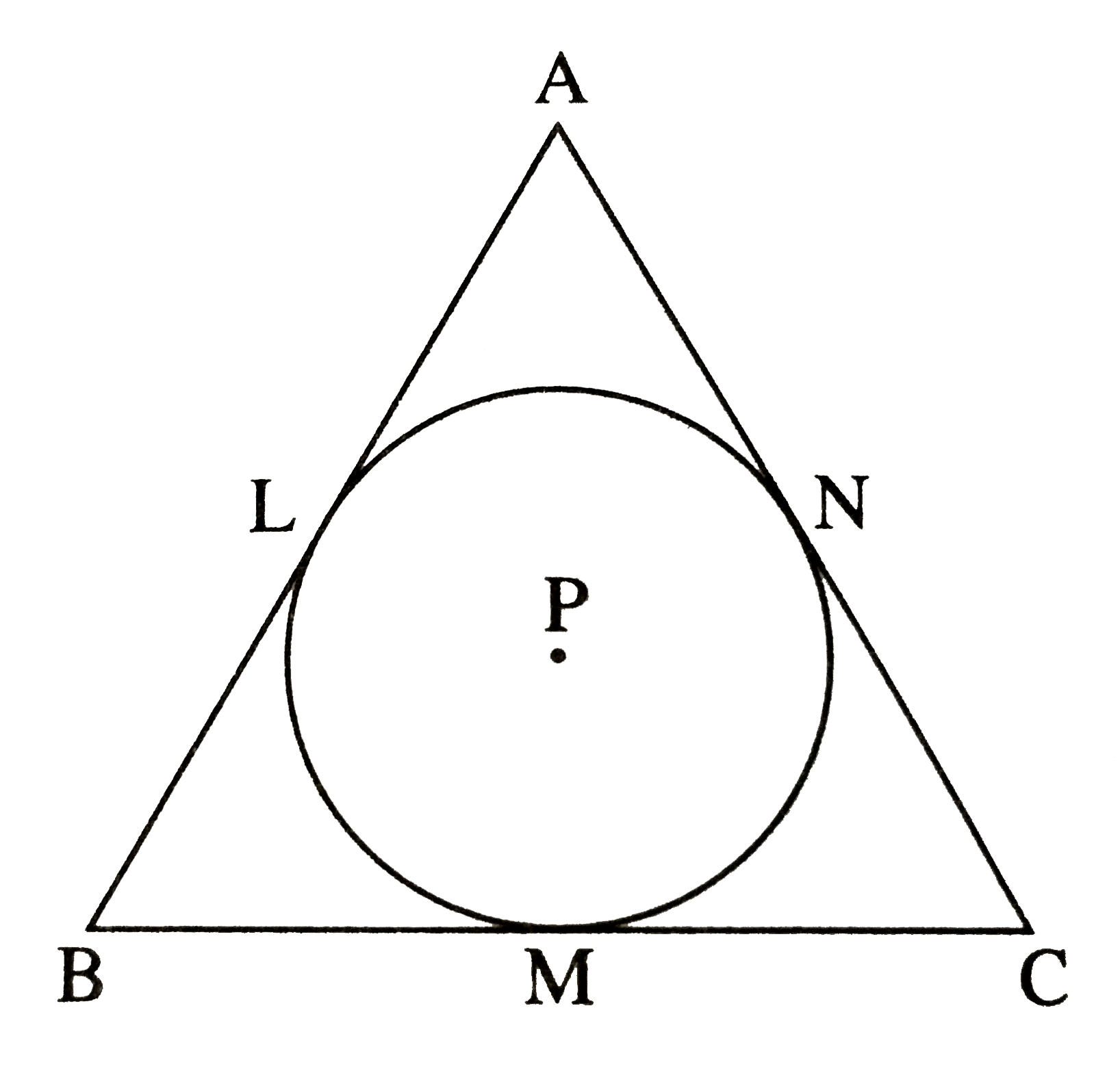
View Solution25. In figure, the sides AB, BC and CA of triangle ABC touch a circle with centre and radius r at P, Q and R respectively. Prove that (i ) AB+CQ=AC+BQ (ii) Area ΔABC=12 perimeter of ΔABC).r.
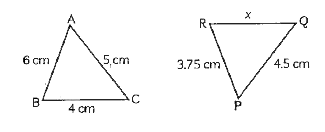
View SolutionIn the given figure ΔABC−ΔPQR. Find the value of x.
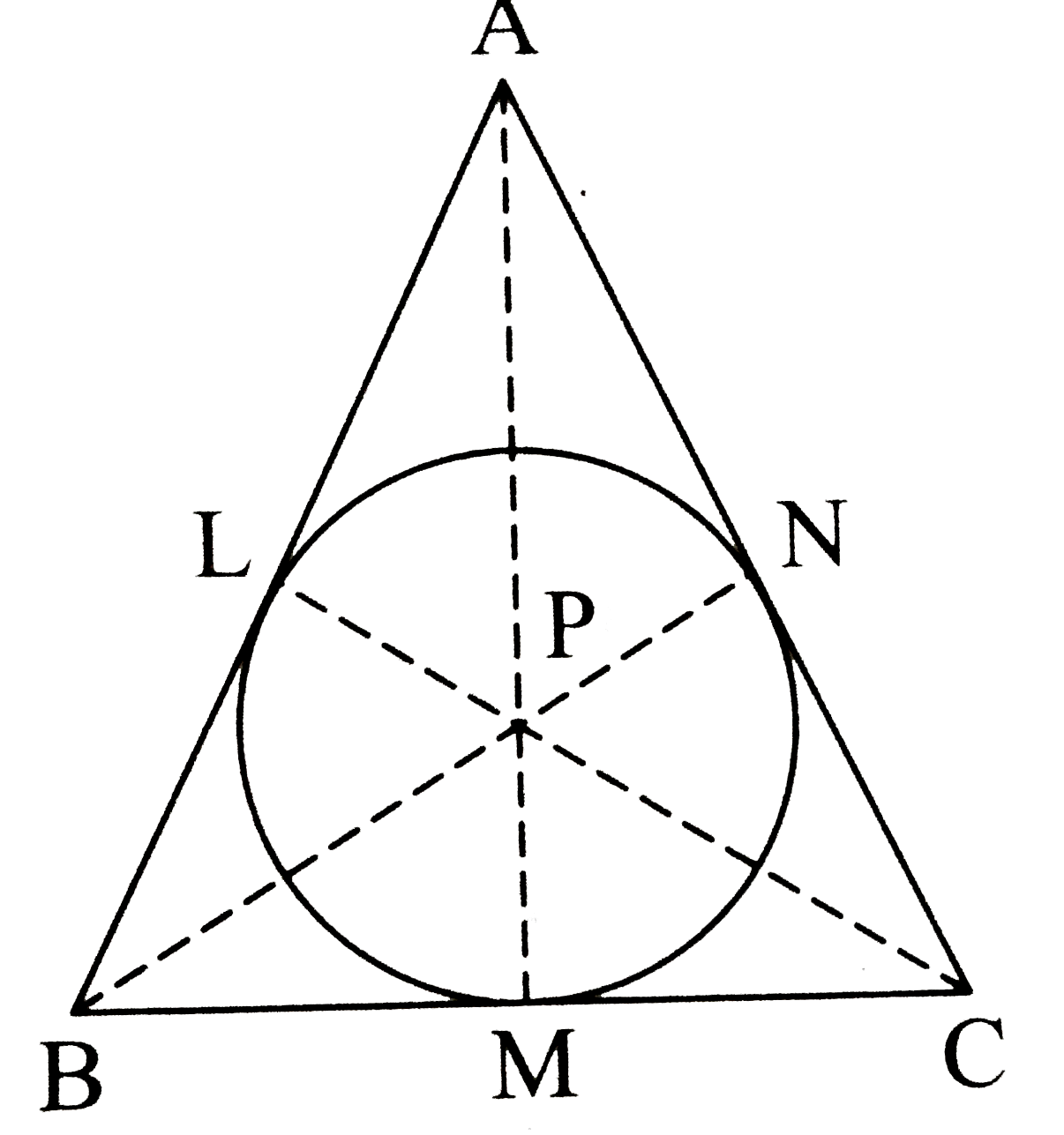
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionState the type of circle which touches all the sides of a triangle and the circle passing through all the vertices of a triangle.
View Solution