Complete Solutions to SHORT ANSWER TYPE QUESTIONS of chapter SOME APPLICATIONS OF TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SOME APPLICATIONS OF TRIGONOMETRY |
| SUPPORT MATERIAL | SHORT ANSWER TYPE QUESTIONS |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
In the figure, find the value of BC.

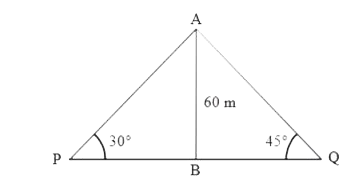
View SolutionIn the figure, two persons are standing at the opposite direction P & Q of the tower. If the height of the tower is 60 m then find the distance between the two persons.
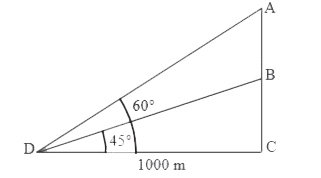
View SolutionIn the figure, find the value of AB.
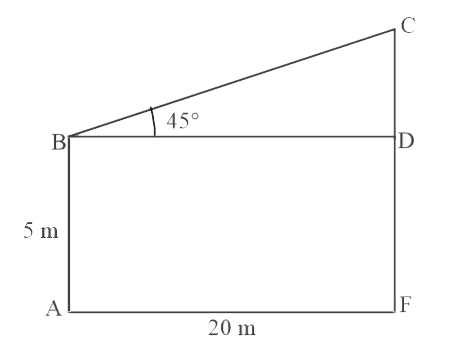
View SolutionIn the figure, find the value of CF.
View SolutionIf the horizontal distance of the boat from the bridge is 25 m and the height of the bridge is 25 m, then find the angle of depression of the boat from the bridge.
View SolutionState True/False.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
View SolutionIf a man standing on a plat form 3 m above the surface of a lake observes a cloud and its reflection in the lake at this time the height of reflection of cloud in lake is (h+3) because in lake platform height is also added to reflection of cloud.
So, angle of depression is different in the lake from the angle of elevation of the cloud is equal to the angle of depressin of its reflection.
View SolutionThe angle of elevation of the top of a tower is `30^(@)`. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
View SolutionFrom the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be `30^0a n d45^0` . Find the height of the hill.
View SolutionThe string of a kite is 150 m long and it makes an angle `60^(@)` with the horizontal. Find the height of the kite above the ground. (Assume string to be tight)
View SolutionThe shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from `45^(@)` to `30^(@)`. Find the height of the tower.
View SolutionAn aeroplane at an altitude of 200 m observes angles of depression of opposite points on the two banks of the river to be `45^(@)` and `60^(@)`, find the width of the river.
View SolutionThe angle of elevation of a tower at a point is `45^(@)`. After going 40 m towards the foot of the tower, the angle of elevation of the tower becomes `60^(@)`. Find the height of the tower.
View SolutionThe upper part of a tree broken over by the wind makes an angle of `30^(@)` with the ground and the distance of the root from the point where the top touches the ground is 25 m. What was the total height of the tree?
View SolutionA vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation of its top is found to be `45^(@)`. Find the height of the flagstaff.
View SolutionThe length of a string between kite and a point on the ground is 90 m. If the string makes an angle with the level ground and `sin alpha=(3)/(5)`. Find the height of the kite. There is no slack in the string.
View SolutionAn aeroplane, when 3000 m high, passes vertically above anthoer aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are `45^(@)" and "60^(@)` respectively. Find the vertical distance between the tow planes.
View SolutionA 7 m long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are `45^(@)"and " 30^(@)` respectively. Find the height of the tower.
View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.
View SolutionAnand is watching a circus artist climbing a 20m long rope which is tightly stretched and tied from the top of vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is `30^(@)`.
View Solution
SHORT ANSWER TYPE QUESTIONS questions and complete solutions for chapter SOME APPLICATIONS OF TRIGONOMETRY of CBSE COMPLEMENTARY MATERIAL MATHS (HINGLISH) of Class 10