Complete Solutions to ANSWER THE FOLLOWING QUESTIONS of chapter PRACTICE QUESTION PAPER 13 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | PRACTICE QUESTION PAPER 13 |
| CPC CAMBRIDGE PUBLICATION | ANSWER THE FOLLOWING QUESTIONS |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
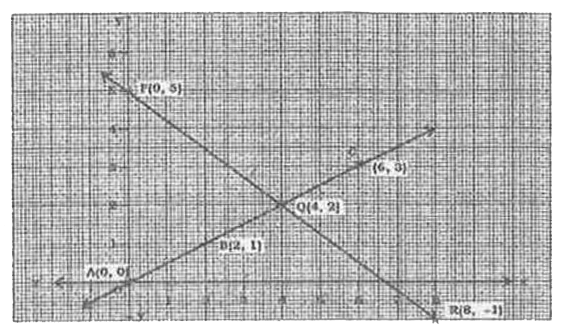
The given graph represents a pair of linear equations in two variables : write how many solutions these pair of equations have
View Solution17 = `6 xx2`+5 is compared with Euclid's Division lemma a = bq +r then which number is representing the remainder
View SolutionFind the zeroes of the polynomial P (x) = `x^(2)-3`
View SolutionWrite the degree of the polynomial P (x) = `2x^(3)-x^(2)+5`
View SolutionFind the value of the discriminant of the quadratic equation `2x^(2)-4x+3=0`
View SolutionWrite the foumula to calculate the curved surface area of the frustum of a cone .
View SolutionFind the sum of first twenty terms of Arithmetic series 2 +7+12 + `cdots ` using suitable formula.
View SolutionIn `Delta` ABC , AD `bot`BC and `AD^(2)= BD xx CD`. Prove that `AB^(2) + AC^(2)`= `(BD + CD)^(2)`

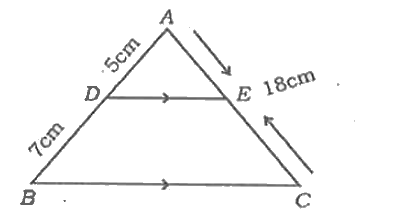
View SolutionIn `Delta` ABC , DE `||` BC . If AD= 5 cm , BD = 7 cm and AC = 18 cm , find the length of AE.
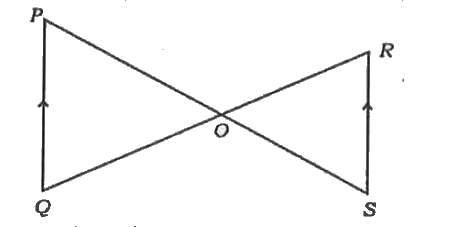
View SolutionIn the given figure PQ `||` RS , prove that `Delta POQ~Delta SOR.`
View SolutionSolve the following pair of linear equations by any suitable method.
x+y = 5 `" "` 2x-3y=5
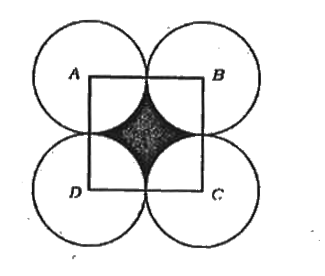
View SolutionIn the figure , ABCD is a square of side 14 cm. A, B, C and D are the centres of four congruent circle such that each circle touches externally two of the remaining three circles . Find the area of the shaded reginon.
View SolutionDraw a circle of radius 4 cm and construct a pair of tangents such that the angle between then is `60^@`.
View SolutionFind the co - ordinates of points which divides the line segment joining the points A `(4,-3)` and B (8,5) in the ratio `3:1` internally .
View SolutionProve that `3+sqrt5` is an irrational number.
View SolutionSolve `2x^(2)`-5x+3 = 0 by using formula.
View SolutionThe length of a rectangular field is 3 time its breadth . If the area of the field is 147 sq.m, find its length and breadth.
View SolutionIf sin `theta = (12)/(13)` find the values of cos `theta` and tan`theta`. `" " (2)`
View SolutionIf `sqrt3 tan theta = 1 and theta` is acute, find the value of `sin 3 theta + cos 2 theta`
View SolutionProve that `((1+cos theta)/(1-cos theta))=("cosec"theta + "cot"theta)^(2)`
View SolutionA cubical die numbered from 1 to 6 are rolled twice . Find the probability of getting the sum of numbers on its faces is 10 .
View SolutionThe radii of two circular ends of a frustum of a cone shaped dustbin are 15 cm and 18 cm . If its depth is 63 cm find the volume of the dustbin
View SolutionProve that "the lengths of tangents drawn from an external points to a circle are equal ".
View SolutionIn the given figure PQ & RS are two parallel tangents to a circle o and another tangent AB with point of contact C intersecting PQ at A and RS at B. Prove that `angleAOB = 90^@`

View SolutionCalculate the median of the following frequency distribution tabel :
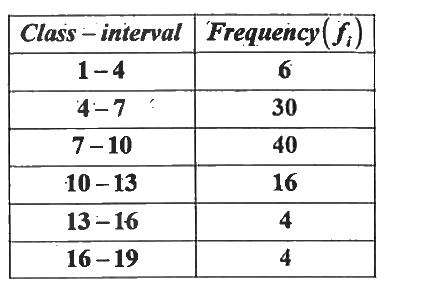
View SolutionCalculate the mode for the following frequency distribution table

View SolutionThe seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression.
View SolutionA line segment is divided into four parts forming an arithmetic progression . The sum of the lengths of 3 rd and 4 th parts is three times the sum of the lengths of first two part. If the length of fourth part is s14 cm, find the total length of the line segment.
View SolutionThe vertices of a `Delta ABC` are A(-3,2) . B (-1,-4) and C(5,2) . If M and N are the mid-points of AB and AC res.ly. Show that 2MN = BC.
View SolutionThe vertices of a `Delta ABC` are A(-5,-1) B(3.-5) , C-(5.2).Show that the area of the `DeltaABC` is four times the area of the triangle formed by joining the mid-points of the sides of the triangle ABC.
View SolutionFind the sol.n of the following pair of linear by the graphical method.
`2x+y=6`
`2x-y=2`
View SolutionThe angle of elevation of the top of a tower from two points at a distance of 4m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
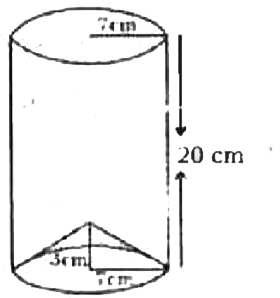
View SolutionThe bottom of a light cylindrical shaped vessel made from metallic sheet is closed by a cone shaped vessel as shown in the figure. The radius of the circular base of the cylinder and radius of the circular base of the cone each is equal to 7 cm . If the height of the cylinder is 20 cm & height of the cone is 3 cm, calculate the cost of milk of fill completely this vessel at the rate of Rs. 20/liter.
View SolutionA hemispherical vessel of radius 14 cm is filled fiuld with sand. This sand is poured on a ground. The heap of sand forms a conc shape of height 7 cm . Calculate the area of ground occupied by the circular base of the heap of the sand.
View Solution
ANSWER THE FOLLOWING QUESTIONS questions and complete solutions for chapter PRACTICE QUESTION PAPER 13 of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 10