Complete Solutions to EXERCISE 17(A) of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| SELINA PUBLICATION | EXERCISE 17(A) |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
In the given figure. O is the centre of the circle. `angle OAB and angle OCB ` are `30 ^(@) and 40 ^(@) ` respectively . Find ` angle AOC ` . Show your steps of working.

View SolutionIn the given figure `angle BAD = 60 ^(@) ,angle ABD = 70^(@) angle BDC = 45^(@) `
(i) prove that AC is a diameter of the circle
(ii) Find ` angle ACB `
` (##SEL_RKB_ICSE_MAT_X_C17_E02_002_Q01.png" width="80%">
View SolutionGiven O is the centre of the circle and ` angle AOB = 70 ^(@) ` , Calculate the value of
(i) ` angle OCA.`
(ii) ` angle OAC `.

View SolutionIn each of the following figure. O is the centre of the circle. Find the values of a,b and c.

View SolutionIn each of the following figure. O is the centre of the circle . Find the values of a,b c. and d

View SolutionIn the figure , AB is common chord of the two circles. If AC and AD are diameter. Prove that D,B and C are in a straight line. `O_1 and O_2` are the centres of two circles.

View SolutionIn the figure , given below. Find
(i) ` angle BCD `
(ii) ` angle ADC `
(iii) ` angle ABC.`
Show steps of your working.

View SolutionIn the given figure O is the centre of the circle If ` angle AOB = 140 ^(@) and angle OAC = 50^(@) ` , find :
(i) ` angle ACB `
(ii) `angle OBC `
(iii) ` angle OAB `
(iv) ` angle CBA `

View SolutionCalculate :
(i) ` angle CDB `
(ii) ` angle ABC `
(iii) ` angle ACB `

View SolutionIn the figure , given below .ABCD is a cyclic quadrilateral in which ` angle BAD = 75 ^(@) , angle ABD = 58 ^(@) and angle ADC = 77^(@) , ` Find :
(i) ` angle BDC , `
(ii) ` angle BCD .`
(iii) ` angle BCA.`

View SolutionIn the following figure , O is centre of the circle and `Delta ABC ` is equilateral Find :
(i)` angle ADB `
(ii) ` angle AEB`

View SolutionGiven : `angle CAB = 75 ^(@) `
and ` angle CBA = 50 ^(@) ` Find the value of
` angle DAB + angle ABD `.

View SolutionABCD is a cyclic quadrilateral in a circle with centre O.
If ` angle ADC = 130 ^(@) ` , find ` angle BAC ?
View SolutionIn the figure , given alongside , AOB is a diameter of the circle and ` angle AOC = 110 ^(@) ` Find ` angle BDC.`

View SolutionIn the following figure. O is the centre of the circle .
` angle AOB = 60 ^(@) ` and
` angle BDC = 100^(@) `
Find ` angle OBC `.

View SolutionIn cyclic quadrilateral ABCD , `angle DAC = 27^(@) `
` angle ADB = 33 ^(@) `
Calculate :
(i) ` angle DBC `
(ii)` angle DCB `
(iii)` angle CAB .`

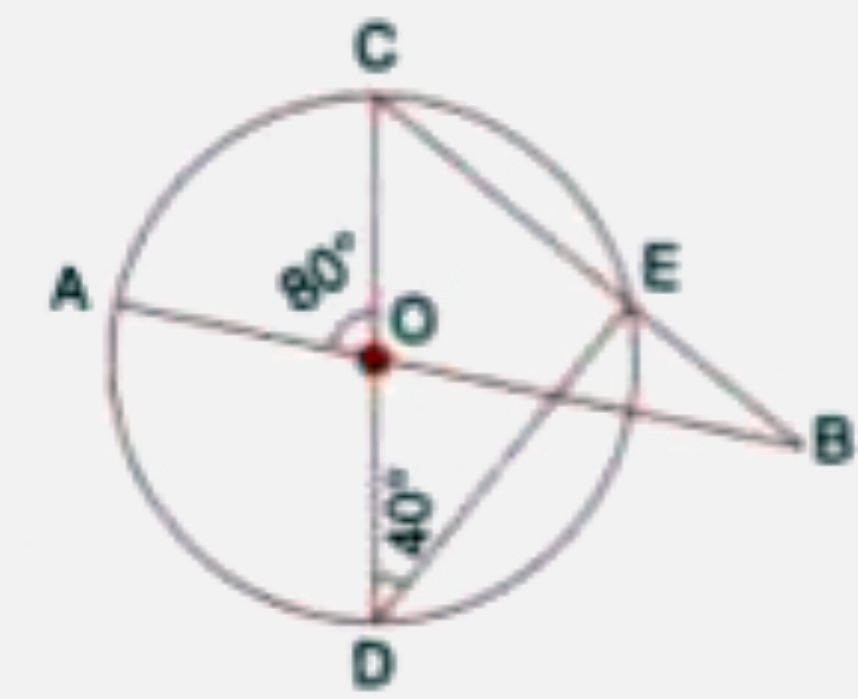
View SolutionIn the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ` angle AOC = 80 ^(@) and angle CDE= 40 ^(@) ` , find ` angle DCE`
View SolutionIn the given figure AC is a diemeter of a circle O, A circle is described on AO as diameter AE, a chord of the larger circle , intersects the smaller circle at B .
Prove that : AB = BE

View SolutionIn the following figure .
(i) if ` angle BAD = 96^(@) , " find " angle BCD and angle BFE. `
(ii) Prove that AD is parallel to PE.
` (##SEL_RKB_ICSE_MAT_X_C17_E02_019_Q01.png" width="80%">
(b) ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q . Show that quadrilateral PCDQ is cyclic.
View SolutionProve that :
the parallelogram , inscirbed in a circle , is a rectangle.
View SolutionProve that :
the rhombus , inscribed in a circle is a square.
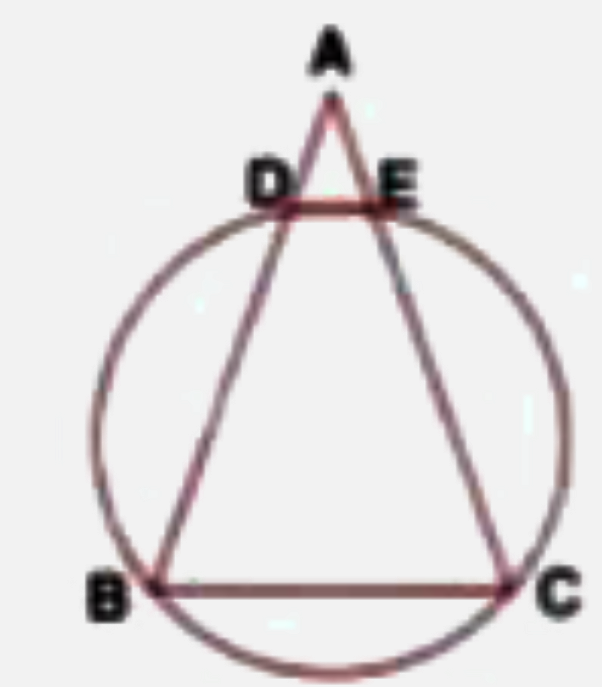
View SolutionIn the given figure AB = AC . Prove that DECB is an isoseles traqezium.
View SolutionTwo cirlces intersect at P and Q . Through P diameter PA and PB of the two circles are drawn. Show that the points A,Q and B are collinear.
View SolutionThe figure given below, shows a circle with centre O.
Given ` : angle AOC = a and angle ABC = b `
Find the relationship between a and b.
(ii) Find the measure of angle OAB ,if OABC is a parallelogram

View SolutionTwo chords AB and CD intersect at P inside the circle . Prove that the sum of the angles substended by the arcs AC and BD at the centre O is equal to twice the angle APC.
View SolutionIn the given figure ,RS is a diameter of the circle NM is parallel to RS and `angle MRS = 29 ^(@) ` Calculate :
(i) ` angle RNM. `
(ii) ` angle NRM `

View SolutionIn the figure , given alongside. AB //CD and O is the centre of the circle. If ` angle ADC = 25^(@) ` find the angle AEB Give reasons in support of your answer.

View SolutionTwo circles intersects at P and Q. through P, a straight line APB is drawn to meet the circles in A and B. Through Q,a straight line is drawn to meet the circles at C and D . Prove that AC is parallel to BD.

View SolutionABCD is a cyclic quadrilateral in which AB and DC on being produced , meet at P such that PA = PD. Prove that AD is parallel to BC .
View SolutionAB is a diameter of the circle APBR at shown in the figure. APQ and RBQ are straight lines
Find :
(i) ` angle PRB `
(ii) ` angle PBR `
(iii) ` angle BPR. `
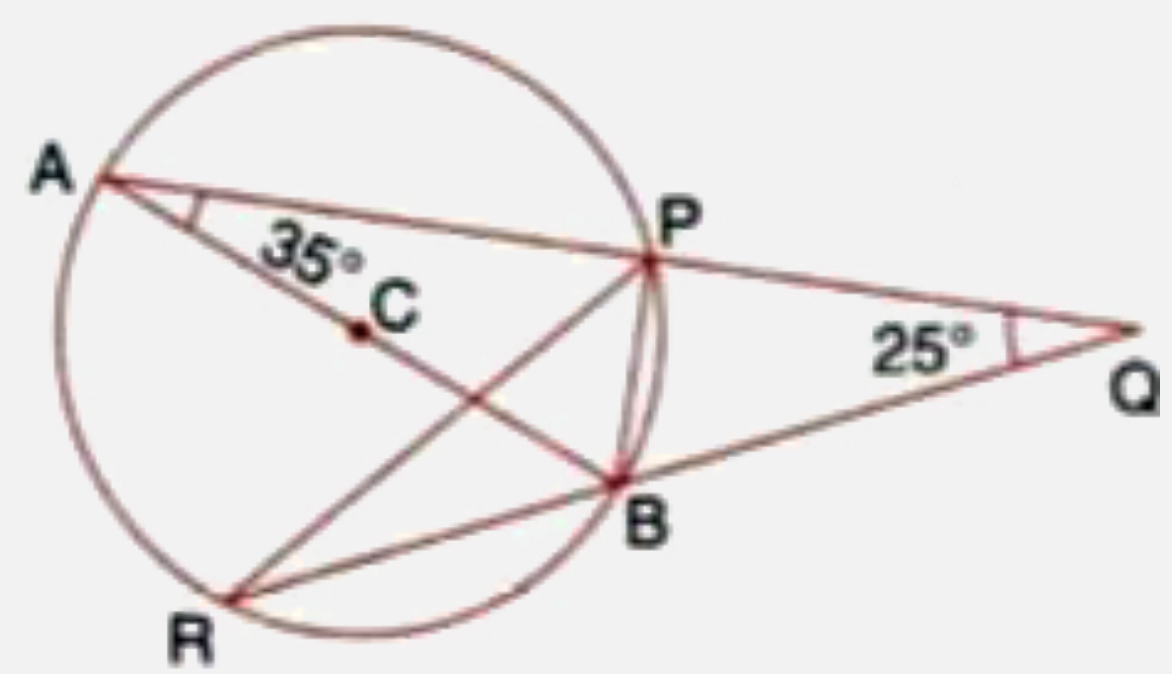
View SolutionIn the given figure . SP is bisector of ` angle RPT ` and PQRS is a cyclic quadrilateral . Prove that SQ = SR

View SolutionIn the figure O is the centre of the circle `angle AOE = 150 ^(@) , angle DAO = 51 ^(@) `. Calculate the sizes of the angles CEB and OCE.
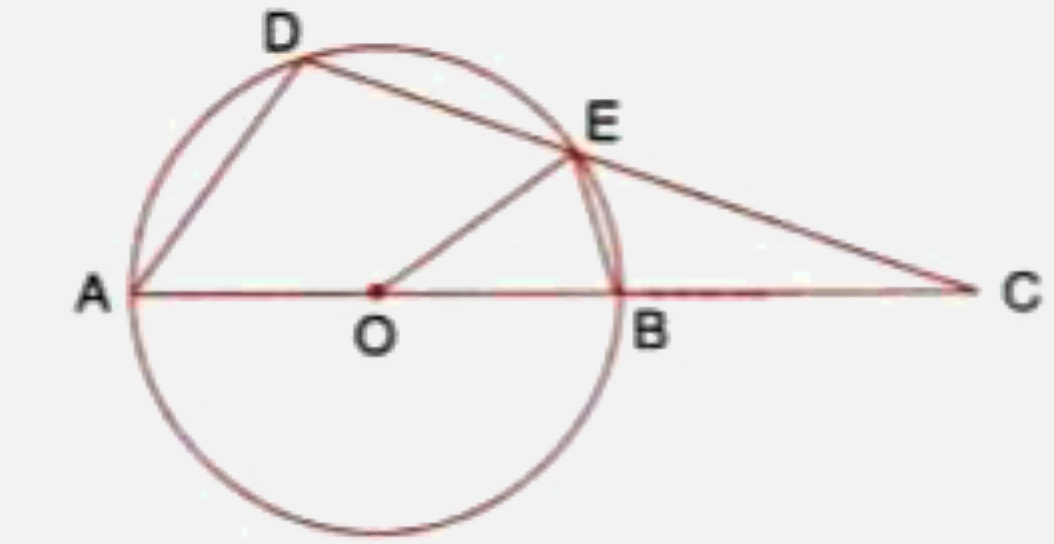
View SolutionIn the figure , given below P and Q are the centres of two circles intersecting at B and C . ACD is a straight line. Calculate the numerical value of x.

View SolutionThe figure shows two circles which intersects at A and B . The centre of the smaller circle is O and lies on the circumference of the Calculate. In terms of ` a^(@) ` , the value of
(i) abtuse ` angle AOB `
(ii) ` angle ADB `
Give reassons for your answers clearly.

View SolutionIn the given figure ,O is the centre of the circle and ` angle DAB = 50 ^(@) ` Calculate the values of x and y.

View SolutionIn the given figure. A is the centre of the circle , ABCD is a parallelogram and CDE is a straight line.
Prove that `: angle BCD = 2 angle ABE `
` (##SEL_RKB_ICSE_MAT_X_C17_E02_036_Q01.png" width="80%">
View SolutionABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ` angle BED = 65^(@) ` , Calculate
(i) ` angle DAB `
(ii) ` angle BDC `
View SolutionIn the given figure AB is a diameter of the circle. Chord ED is parallel to AB and `angle EAB = 63 ^(@) ` Calculate
` (i) angle EBA `
(ii) ` angle BCD `
View SolutionIn the given figure AB is a diameter of the circle with centre O. DO is parallel to CB and ` angle DCB = 120 ^(@) ` Calculate :
(i) ` angle DAB `
(ii) ` angle DBA `
(iii) ` angle DBC, `
(iv) ` angle DBC `
Also , show that the ` Delta ` AOD is an equilateral triangle.

View SolutionIn the given figure, I is the incentre of ` Delta ABC` BI when produced meets the circumcircle of ` Delta ABC ` at D. Given ` angle BAC = 55 ^(@) and angle ACB = 65^(@) , ` Calculate:
(i) ` angle DCA . `
(ii) ` angle DAC `
(iii) ` angle DCI.`
` angle AIC.`

View SolutionA triangle ABC is inscribed in a circle. The bisector of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P,Q and R respectively . Prove that :
(i) ` angle ABC = 2 angle APQ .`
(ii) `angle ACB = 2 angle APR `.
(iii) ` angle QPR = 90 ^(@) -(1)/(2) angle BAC. `

View SolutionCalculate the angles x,y and z if
` (x)/(3) = (y)/(4) =(z)/(5)`
` (##SEL_RKB_ICSE_MAT_X_C17_E02_042_Q01.png" width="80%">
View SolutionIn the given figure , AB = AC = CD and ` angle ADC = 38^(@) ` . Calculate :
(i) ` angle ABC `
(ii) ` angle BEC `

View SolutionIn the given figure ,AC is the diameter of circle , centre O. Chord BD is perpendicular to AC. Write down angles p,q and r in terms of x.

View SolutionIn the given figure ,AC is the diameter of the circle with centre O,CD and BE are parallel Angle ` angle AOB = 80 ^(@) and angle ACE = 10 ^(@) ` Calculate
(i) Angle BEC
(ii) Angle BCD,
(iii) Angle CED

View SolutionIn the given figure . AE is the diamter of the circle . Write down the numerical value of `angle ABC + angle CDE . ` Give reasons for your answers.

View SolutionIn the given figure. AOC is a diameter and AC is parallel to ED . If ` angle CBE = 64^(@) ` calculate ` angle DEC.`

View SolutionUse in the given figure to find :
(i) ` angle BAD .`
(ii) ` angle DQB `

View SolutionIn the given figure , AOB is a diameter and DC is parallel to AB . If ` angle CAB = x^(@) , ` find (in terms of x) the values of :
(i) ` angle COB `
(ii) ` angle DOC `
(iii) ` angle DAC `
(iv) ` angle ADC. `
View SolutionIn the given figure ,AB is the diameter of a circle with centre O. ` angle BCD = 130 ^(@) ` Find :
(i) ` angle DAB `
(ii) ` angle DBA `

View SolutionIn the given figure, PQ is the diameter of the circle whose centre is O. Given ` angle ROS = 42^(@) ` Calculate ` angle RTS .`

View SolutionIn the given figure, PQ is a diameter Chord SR is parallel to PQ . Given that ` angle PQR = 58^(@) ` Calculate:
(i) ` angle RPQ `
(ii) ` angle STP `

View SolutionAB is the diameter of the circle with centre O. OD is parallel to BC and ` angle AOD = 60 ^(@) `
Calculate the numerical values of :
(i) `angle ABD `
(ii) ` angle DBC `
(iii) ` angle ADC `.

View SolutionIn the given figures , the centre O of the small circle lies on the circumference of the bigger circle. If ` angle APB = 75^(@) and angle BCD = 40 ^(@) ` find :
(i) ` angle AOB `
(ii) ` angle ACB .`
(iii) ` angle ABD .`
(iv) ` angle ADB .`

View SolutionIn the given figures , `angle BAD = 65 ^(@) , angle ABD = 70 ^(@) and angle BDC = 45^(@) `, Find :
(i) ` angle BCD `
(ii) ` angle ACB `
Hence , show that AC is a diameter

View SolutionIn a cyclic quadrilateral ABCD ` angle A : angle C = 3: 1 and ` angle B : angle D = 1 : 5 ` find each angle of the quadrilateral
View SolutionThe given figures shows a circle with centre O and ` angle ABP = 42 ^(@) `

Calculate the measure of :
(i) ` angle PQB`
(ii) ` angle QPB + angle PBQ `
View SolutionIn the given figure, M is the centre of the circle Chords AB and CD are perpendicular to each other. If ` angle (i) express ` angle AMD ` in terms of x.
(ii) express ` angle ABD ` in terms of y .
(iii) Prove that : x=y

View Solution
EXERCISE 17(A) questions and complete solutions for chapter CIRCLES of SELINA MATHS (ENGLISH) of Class 10