Complete Solutions to QUESTIONS of chapter CYLINDER, CONE AND SPHERE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CYLINDER, CONE AND SPHERE |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
The area of the curved surface of a cylinder is `4,400 cm^(2)` and the circumference of its base is 110 cm. Find :
(i) the height of the cylinder,
(ii) the volume of the cylinder.
View Solution50 identical circular plates are placed one above the other to form a solid cylinder. For each plate, diameter = 21 cm and thickness = 15 cm. Find :
(i) curved surface area of the cylinder formed.
(ii) volume of the cylinder fomred.
View SolutionThe volume of a solid cylinder is `96228 cm^(3)` and the ratio of its radius to its height is 9:14. Find the total surface area of the cylinder.
View SolutionA cylindrical tube, open at both ends, is made of metal. The internal diameter of the tube is 112 cm and its length is 21 cm. The metal everywhere is 0.4 cm in thickness. Calculate the volume of the metal correct to one place of decimal.
View SolutionFind the volume of the largest cylinder formed when a rectangular piece of paper 22 cm by 15 cm is rolled along its longer side.
View SolutionWhen a metal cube is completely submerged in water contained in a cylindrical vessel with diameter 30 cm, the level of water rises by `1 (41)/(99) cm.` Find :
(i) the length of edge of the cube.
(ii) the total surface area of the cube.
View SolutionThe radius of the base and the height of a right circular cone are 7 cm and 24 cm respectively. Find the volume and the total surface area of the cone.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
View SolutionThe ratio of the base area and the curved surface area of a conical tent is 40:41. If its height is 18 m, find the air capacity of the tent in terms of `pi.`
View SolutionFind what length of canvas, 2 m in width, is required to make a conical tent 12 m in diameter and 63 m in slant height?
Also, find the cost of the canvas at the rate of Rs. 150 per metre.
View SolutionA vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 20 cm and diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged ?
View SolutionFind the area of the canvas required to make a conical tent 14 m high and 96 m in diameter. Given that:
(i) 20% of the canvas is used in folds and stitchings.
(il) canvas used in folds and stitchings is 20% of the curved surface area of the tent.
View SolutionThe capacity and the base area of a right circular conical vessel are 9856 `cm^(3)` and 616 `cm^(2)` respectively. Find the curved surface area of the vessel.
View SolutionIf the surface area of a sphere is 616 `cm^(2),` find its volume.
View SolutionThe internal and external diameters of a hollow hemispherical vessel are 42 cm and 45 cm respectively. Find its capacity and also its outer curved surface area.
View SolutionA solid spherical ball of iron with radius 6 cm is melted and recast into three solid spherical balls. The radii of the two balls are 3 cm and 4 cm respectively, determine the diameter of the third ball.
View SolutionThe internal and external diameters of a hollow hemispherical vessel are 21 cm and 25.2 cm respectively. Find the cost of painting it, all over, at the rate of 1.50 per `cm^(2).`
View SolutionThe radius of the base of a cone and the radius of a sphere are the same, each being 8 cm. Given that the volumes of these two solids are also the same, calculate the slant height of the cone.
View SolutionA metallic sphere of radius 10.5 cm is melted and then recast into small cones each of radius 3.5 cm and height 3 cm. Find the number of cones thus formed.
View SolutionA hollow metal sphere of internal and external radii 2 cm and 4 cm respectively is melted into a solid cone of base radius 4 cm. Find the height and slant height of the cone.
View SolutionA vessel is in the form of an inverted cone. Its height is 11 cm and the radius of its top, which is open, is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm, are dropped into the vessel `(2)/(5)` of the water flows out. Find the number of lead shots dropped into the vessel.
View SolutionA toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm. Determine the surface area and the volume of the toy `(pi = 3.14).`
View SolutionThe given block is made of two solids : a cone and a hemisphere. If the height and the base-radius of the cone are 24 cm and 10 cm respectively and the diameter of the hemisphere is 10 cm, find the total surface area of the block. (Take `pi = 3.14`)

View SolutionThe height of a solid cone is 30 cm. A small cone is cut off from the top of it such that the base of the cone cut off and the base of the given cone are parallel to each other. If the volume of the cone cut and the volume of the original cone are in the ratio 1:27, find the height of the the remaining part of the given cone.
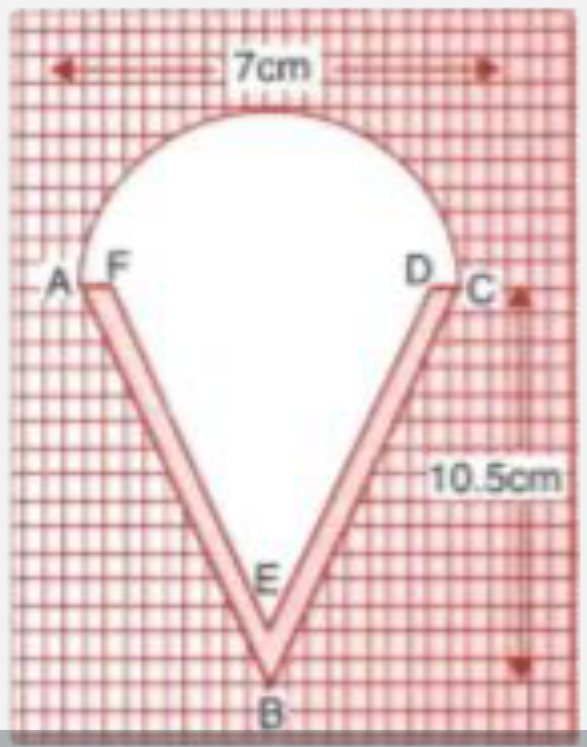
View SolutionThe given figure shows the cross-section of an ice cream cone consisting of a cone surmounted by a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 10-5 cm. The outer shell ABCDEF is shaded and is not filled with ice-cream. AF = DC = 0.5 cm, AB // FE and BC // ED. Calculate :
(i) the volume of the ice-cream in the cone (the internal volume of the cone including the hemisphere) in `cm ^(3),`
(ii) the volume of the outer shell (the shaded portion) in `cm ^(3).`
In each case, give your answer correct to the nearest `cm ^(3).`
View SolutionFrom a solid cylinder of height 36 cm and radius 14 cm, a conical cavity of radius 7 cm and height 24 cm is drilled out. Find the volume and the total surface area of the remaining solid.
View SolutionA girl fills a cylindrical bucket 32 cm in height and 18 cm in radius with sand. She empties the bucket on the ground and makes a conical heap of the sand. If the height of the conical heap is 24 cm, find :
(i) the radius and
(ii) the slant height of the heap. Give your answer correct to one place of decimal.
View SolutionFrom a solid cylinder, whose height is 8 cm and radius is 6 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume of the remaining solid.
View SolutionA cylindrical beaker, whose base has a radius of 15 cm, is filled with water up to a height of 20 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the beaker. Find the increase in the level of water.
View SolutionThe cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
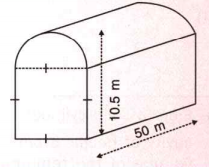
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per `m^(2).`
View SolutionWater flows through a cylindrical pipe of internal diameter 7 cm at 5 metre per second. Calculate :
(i) the volume, in litres, of water discharged by the pipe in one minute,
(ii) the time, in minutes, the pipe would take to fill an empty rectangular tank `4m xx 3m xx 2.31 m.`
View Solution
QUESTIONS questions and complete solutions for chapter CYLINDER, CONE AND SPHERE of SELINA MATHS (ENGLISH) of Class 10