Complete Solutions to Exercise 22 B of chapter HEIGHTS AND DISTANCES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | HEIGHTS AND DISTANCES |
| SELINA PUBLICATION | Exercise 22 B |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
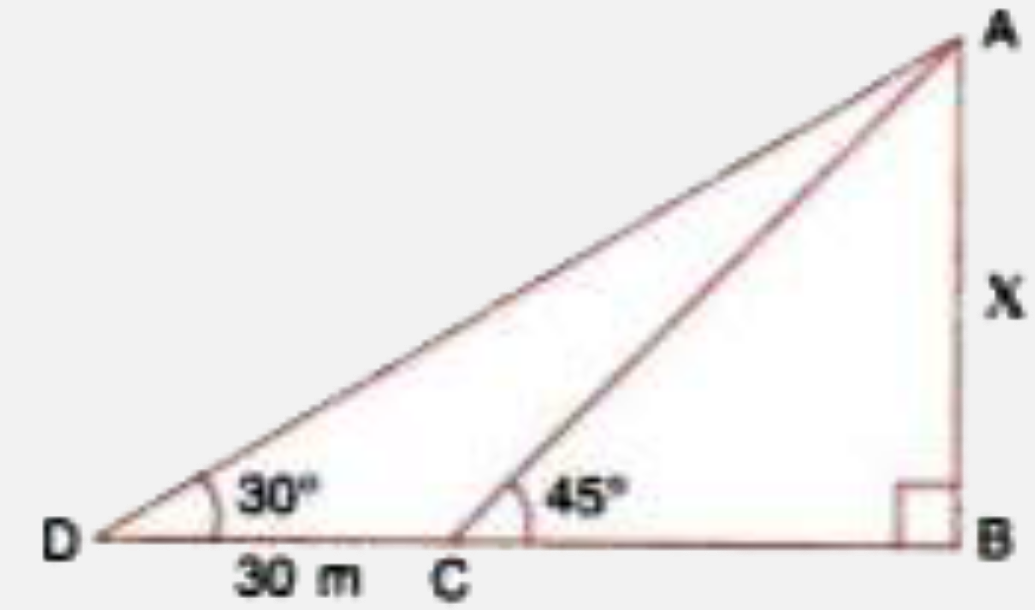
In the figure, given below, it is given that AB is perpendicular ot BD and is of length X metres. DC = 30 m, `angle ADB = 30^(@) and angle ACB = 45^(@)`. Without using tables, find X
View SolutionFind the height of a tree it is found that on walking away from is 20 m, in a horizontal line through is base , the elevation of its top changes from `60^(@) t o 30^(@)`
View SolutionFind the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from `30^(@) t o 45^(@)`
View SolutionFrom the top of a light house 100 m high, t he angles of depression of two ships are observed as `48^(@) and 36^(@)` respectively. Find the distance between the two ships (in the nearest metre ) if :
the ships are on the same side of the light house.
View SolutionFrom the top of a light house 100 m high, t he angles of depression of two ships are observed as `48^(@) and 36^(@)` respectively. Find the distance between the two ships (in the nearest metre ) if :
the ships are on the same side of the light house.
View SolutionTwo pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are `60^(@) and 30^(@)` . Find the height of the pillars and the position of the point
View SolutionFrom the figure, given below . calculate the length of CD

View SolutionThe angle of elevation of the top of a tower is observed to be `60^(@)` . At a point , 30 m vertically above the first point of observation, the elevation is found to be `45^(@)` . Find :
the height of the tower
View SolutionThe angle of elevation of the top of a tower is observed to be `60^(@)` . At a point , 30 m vertically above the first point of observation, the elevation is found to be `45^(@)` . Find :
its horizontal distance from the points of observation.
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be `30o` and `60o` . Find the height of the tower.
View SolutionA man on a cliff observes a boat, at an angle of depression `30^(@)` , which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be `60^(@)` . Assuming that the boat sails at a uniform speed, determine.
how much more time it will take to reach the shore ?
View SolutionA man on a cliff observes a boat, at an angle of depression `30^(@)` , which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be `60^(@)` . Assuming that the boat sails at a uniform speed, determine.
the speed of the boat in metre per second if the height of the cliff is 500 m
View SolutionA man in a boat rowing away from a lighthouse 150 m high, takes2 minutes to change the angle of elevation of the top of the lighthouse from `60^(@)` to `45^(@)` . Find the speed of the boat .
View SolutionA person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is `60^0dot` When he move 40 metres away from the bank, he finds the angle of elevation to be `30^0dot` Find the height of the tree and the width of the river.
View SolutionA person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is `60^0dot` When he move 40 metres away from the bank, he finds the angle of elevation to be `30^0dot` Find the height of the tree and the width of the river.
View SolutionThe horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as see from the top of the second, which is 160 m high, is `45^(@)` . Find the height of the first tower.
View SolutionThe length of the shadow of a tower standing of level plane is found to be 2y metres longer when the sun's altitude is `30^(@)` then when it was `45^(@)` . Prove that the height of the tower is `y (sqrt(3) + 1)` metres
View SolutionAn aeroplane flying horizontally 1 km above the ground is observed at an elevation of `60o` . After 10 seconds, its elevation is observed to be `30o` . Find the speed of the aeroplane in km/hr.
View SolutionFrom the top of a hill, the angles of depression of two consecutive kilometre stones, due east, are found to be `30^(@) and 45^(@)` respectively. Find the distance of the two from the foot of the hill
View Solution
Exercise 22 B questions and complete solutions for chapter HEIGHTS AND DISTANCES of SELINA MATHS (ENGLISH) of Class 10