Complete Solutions to QUESTIONS of chapter QUESTION PAPER 2022 TERM 1 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUESTION PAPER 2022 TERM 1 |
| ICSE | QUESTIONS |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
If `(x + 2)` is a factor of the polynomial `x^3 – kx^2 - 5x + 6` then the value of k is:
View SolutionThe solution set of the inequation `x - 3 ge -5, x in R` is
View SolutionThe product AB of two matrices A and B is possible if:
View SolutionIf 70, 75,80,85 are the first four terms of an Arithmetic Progression, then the `10^(th)` term is:
View SolutionThe selling price of a shirt excluding GST is Rs. 800. If the rate of GST is 12% then the total price of the shirt is:
View SolutionWhich of the following quadratic equations has 2 and 3 as its roots?
View SolutionIf x, 5.4,5,9 are in proportion then x is:
View SolutionIn the given figure `AB = 24 cm, AC = 18 cm. DE = 12cm. DF = 9 cm `and `/_BAC = /_EDF`. Then `DeltaABC ~ DeltaDEF `by the condition:

View SolutionIf `A = [(5,10),(3,-4)] and I = [(1,0),(0,1)]` then `AI` is equal to
View SolutionThe polynomial `x^3 - 2x^2 + ax + 12` when divided by `(x+1)` leaves a remainder 20, then 'a' is equal to:
View SolutionIn an Arithmetic Progression (A.P.) if, first term is 5, common difference is - 3 and the `n^(th)` term is - 7, then n is equal to:
View SolutionIn the given figure PQ is parallel to TR, then by using condition of similarity:
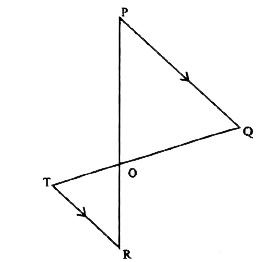
View SolutionIf a, b, c, and d are proportional then `(a + b)/(a - b)` is equal to:
View SolutionThe first four terms of an Arithmetic Progression (A. P.), whose first term is 4 and common difference is – 6, are:
View SolutionOne of the roots of the quadratic equation `x^2 – 8x+ 5 = 0 `is 7.3166. There correct to 4 significant figures is:
View Solution`(x + 2) and (x + 3)` are two factors of the polynomial `x^3 + 6x^2 + 11x + 6`. If polynomial is completely factorised in
View SolutionThe sum of the first 20 terms of the Arithmetic Progression 2, 4, 6, 8, ........... is:
View SolutionThe solution set on the number line of the linear inequation:
`2y-6 < y + 2 <= 2y,y in N` is
View SolutionIf x, y, z are in continued proportion then `(y^2 + z^2): (x^2 + y^2)` is equal to
View SolutionThe marked price of an article is Rs. 5000. The shopkeeper gives a discount of 10%. If the face of GST is 12%, then the amount paid by the customer including GST is:
View SolutionIf `A = [(3,5),(1,4)], B = [(2,4),(0,3)] and C = [(1,-1),(2,1)]` , then 5A - BC is equal to :
View SolutionIn the given figure ABCD is a trapezium in which DC is parallel to AB.
AB = 16 cm and DC = 8 cm. OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x - 1) cm.
Using the given information answer the following questions.
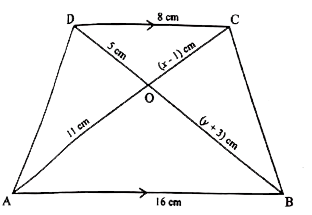
From the given figure name the pair of similar triangles:
View SolutionIn the given figure ABCD is a trapezium in which DC is parallel to AB.
AB = 16 cm and DC = 8 cm. OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x - 1) cm.
Using the given information answer the following questions.
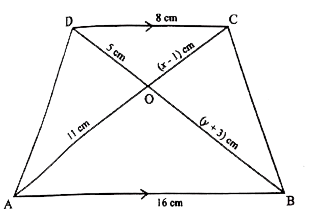
The corresponding proportional sides with respect to the pair of similar triangles obtained in (i)
View SolutionIn the given figure ABCD is a trapezium in which DC is parallel to AB.
AB = 16 cm and DC = 8 cm. OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x - 1) cm.
Using the given information answer the following questions.
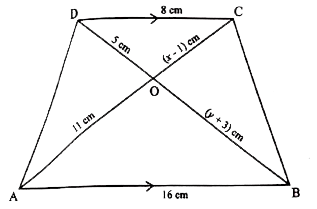
The ratio of the sides of the pair of similar triangles is:
View SolutionIn the given figure ABCD is a trapezium in which DC is parallel to AB.
AB = 16 cm and DC = 8 cm. OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x - 1) cm.
Using the given information answer the following questions.
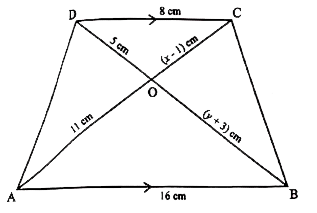
Using the ratio of sides of the pair of similar triangles the values of x and y are respectively
View SolutionTwo cars X and Y use 1 litre of diesel to travel x km and (x + 3) km respectively. both the cars covered a distance of 72 km, then:
the number of litres of diesel used by car X is:
View SolutionTwo cars X and Y use 1 litre of diesel to travel x km and (x + 3) km respectively. both the cars covered a distance of 72 km, then:
The number of liters of diesel used by car Y is :
View SolutionTwo cars X and Y use 1 litre of diesel to travel x km and (x + 3) km respectively. both the cars covered a distance of 72 km, then:
If car X used 4 litres of diesel more than car Y is the journey , then
View SolutionTwo cars X and Y use 1 litre of diesel to travel x km and (x + 3) km respectively. both the cars covered a distance of 72 km, then:
If car X used 4 litres of diesel more than car Y is the journey The amount of diesel used by the car X is:
View SolutionJoseph has a recurring deposit account in a bank for two years at the rare of 8% per annum simple interest.
If at the time of maturity Joseph receives Rs. 2000 as interest then the monthly installment is:
View SolutionJoseph has a recurring deposit account in a bank for two years at the rare of 8% per annum simple interest.
The total amount deposited in the bank:
View SolutionJoseph has a recurring deposit account in a bank for two years at the rare of 8% per annum simple interest.
The amount Joseph receives on maturity is:
View SolutionJoseph has a recurring deposit account in a bank for two years at the rare of 8% per annum simple interest .
If the monthly instalment is Rs. 100 and the rate of interest is 8%, in how many months Joseph will receive Rs. 52 as interest?
View Solution
QUESTIONS questions and complete solutions for chapter QUESTION PAPER 2022 TERM 1 of SELINA MATHS (ENGLISH) of Class 10