Complete Solutions to EXAMPLE of chapter QUESTION PAPER FEB 2019 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUESTION PAPER FEB 2019 |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
Consider the arithmetic sequence 13,23,33,... What is its common difference?
View SolutionConsider the arithmetic sequence 13,23,33,... What is the first three digit term of this sequence?
View SolutionIn the figure, O is the centre of the circle `squareA=60^o`.
`squareBOD`=______
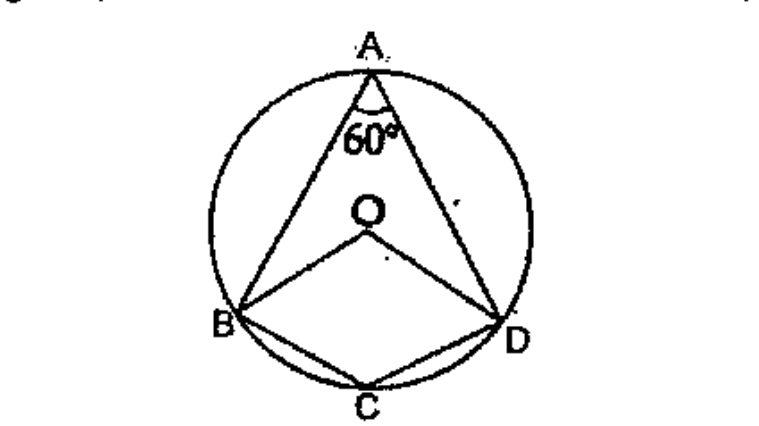 .
.
View SolutionIn the figure, O is the centre of the circle `squareA=60^o`.
`squareC`=______
 .
.
View SolutionIf `x-1` is a factor of the polynomial `5x^3-4x^2+x-k`,what number is k?
View SolutionA circle is drawn with the origin as centre. It passes through the point `(3,3)`.
What is the radius of the circle?
View SolutionA circle is drawn with the origin as centre. It passes through the point `(3,3)`.
Write the co-ordinates of a point where the circle meets the `x`-axis.
View SolutionIf a square is inscribed in a circle of diameter 4 cm, what will be the length of a side of the square?
View SolutionWhat is the base edge of a square pyramid of maximum size that can be carved out from a hemisphere of radius 5 cm?
View SolutionDraw the co-ordinate axes and mark the point `(4,0)`. Draw an isosceles right angled triangle with this point as one of its vertices.
View SolutionDraw a cercle of radius 3.5 centimetres. Draw a triangle of angles `50^o`,`60^o`,`70^0` with its vertices as points on the circle.
View SolutionThe algebraic form of an arithmetic sequence is `5n+5` What is its first term?
View SolutionThe algebraic form of an arithmetic sequence is `5n+5` What is the difference of its `10^(th)` and `20^(th)` terms?
View SolutionThe algebraic form of an arithmetic sequence is `5n+5` Can the difference of any two terms of this sequence be 368? Justify.
View SolutionThe length of a rectangle is 6 centimetres more than its breadth. Its area is 1216 square centimetres. Find its length.
View SolutionIn the figure, C,D are points on the circle AD is a diameter of the circle. `squareC=30^o`.`AB=4` centimetres.
`squareD`=_______
 .
.
View SolutionIn the figure, C,D are points on the circle AD is a diameter of the circle. `squareC=30^o`.`AB=4` centimetres.
`squareABD`=_____
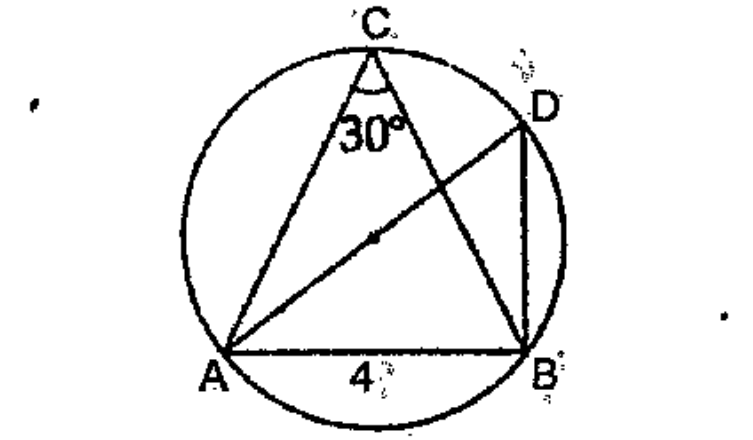 .
.
View SolutionIn the figure, C,D are points on the circle AD is a diameter of the circle. `squareC=30^o`.`AB=4` centimetres.
What is the length of the diameter?
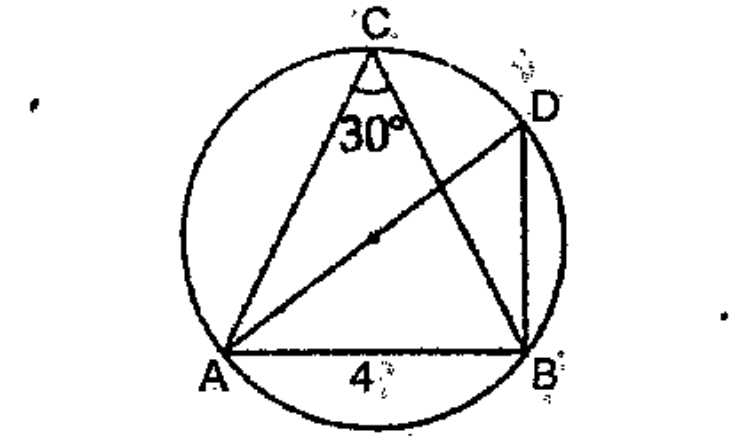 .
.
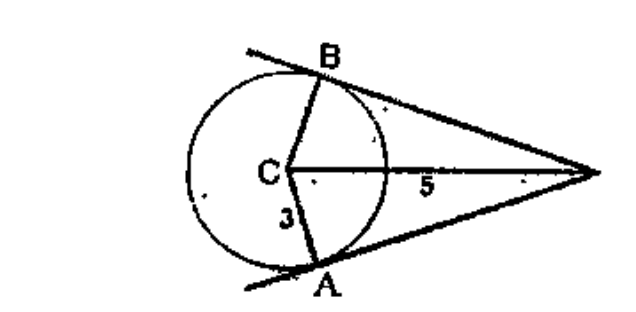
View SolutionIn the figure C is the centre of the circle, PA and PB are tangents. `PC=5` centimetres and radius of the circle is 3 centimetres.
Find the length of PA
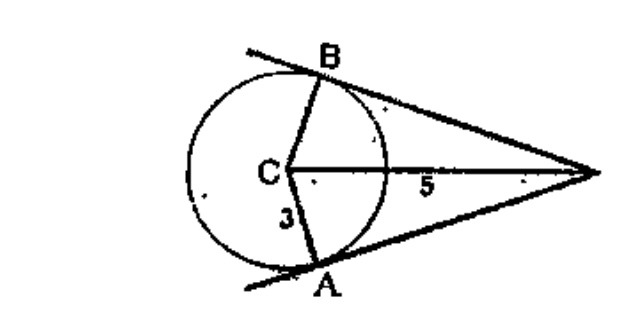 .
.
View SolutionIn the figure C is the centre of the circle, PA and PB are tangents. `PC=5` centimetres and radius of the circle is 3 centimetres.
What is the area of the quadrilateral PACB.
 .
.
View SolutionThe co-ordinates of two opposit vertices of a rectangle are `(7,8)` and (1,3)`.
Find the co-ordinates of other two vertices.
View SolutionThe co-ordinates of two opposite vertices of a rectangle are `(7,8)` and (1,3)` What is the length of its diagonals?.
View SolutionConsider the polynomial `P(x)=ax^3-x^2-bx-1`.Find `P(1)`.
View SolutionConsider the polynomial `P(x)=ax^3-x^2-bx-1`.What is the relation between a and b if `x-1` is a factor of `P(x)`?
View SolutionConsider the polynomial `P(x)=ax^3-x^2-bx-1`.What is the relation between a and b if `x+1` is a factor of `P(x)`?
View SolutionConsider the polynomial `P(x)=ax^3-x^2-bx-1`
Will, `P(x)` have both `(x+1)` and `(x-1)` as factors for any numbers a and b? Justify.
View SolutionThe radius and height of a cone are 12 centimetres and 6 centimetres respectively.What is its volume?
View SolutionThe radius and height if a cone are 12 centimetres and 6 centimetres respectively.
If this cone is cut parallel to its base, along the midpoint of its height, what is the radius of the small cone obtained?
View SolutionThe radius and height if a cone are 12 centimetres and 6 centimetres respectively.
What is the volume of the small cone?
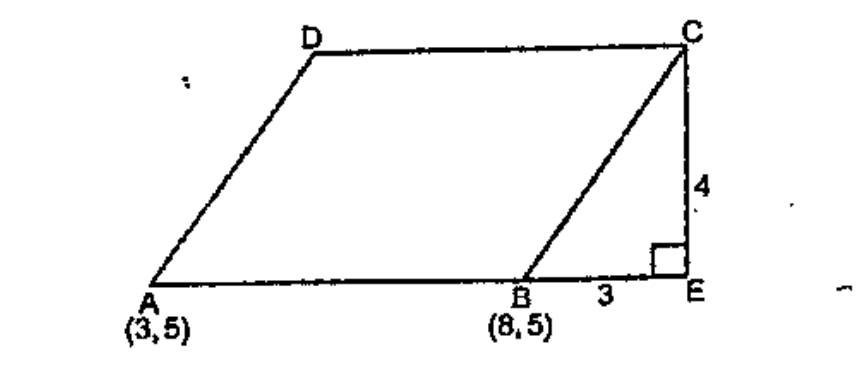
View SolutionIn the figure `ABCD` is a parallelogram. `squareE=90^o`. `A(3,5) B(8,5)` are two vertices `BE=3 units`, `CE=4 units`.
Write the coordinates of C.
 .
.
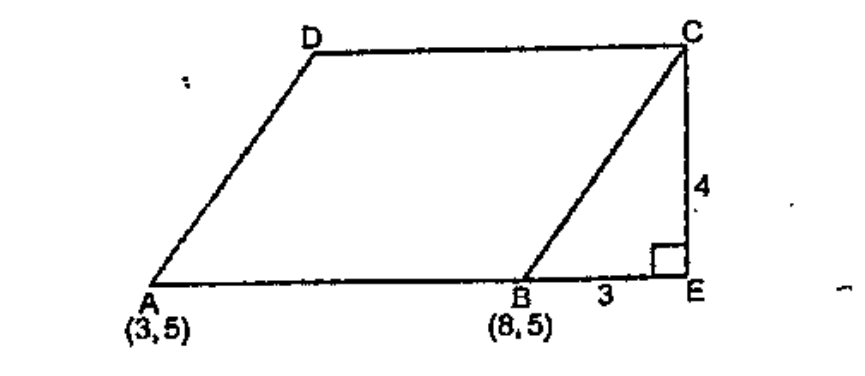
View SolutionIn the figure `ABCD` is a parallelogram. `squareE=90^o`. `A(3,5) B(8,5)` are two vertices `BE=3 units`, `CE=4 units`.
What are the coordinates of D?
 .
.
View SolutionDraw a circle of radius 3 centimetres,mark a point 7 centimetres away from its centre. Draw the tangents to the circle from that point.
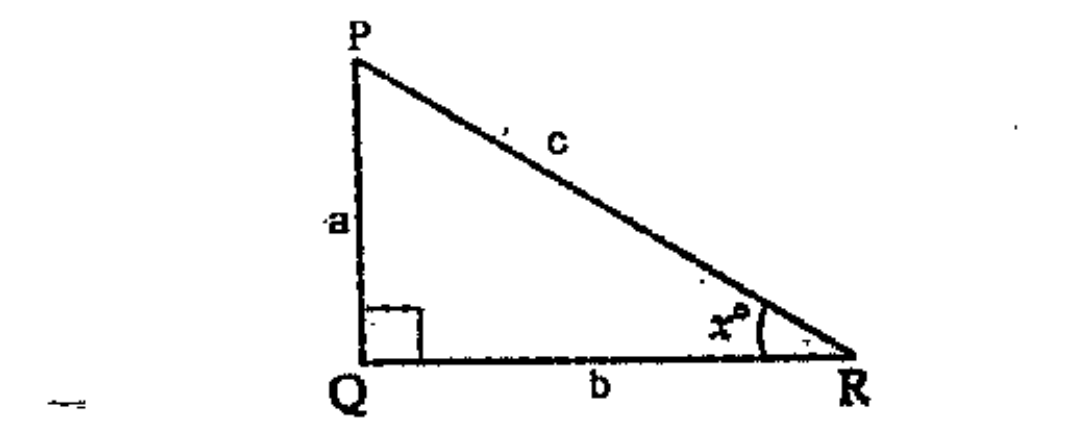
View SolutionIn triangle `PQR,`squareQ=90^o`, `squareR=x^o`. Lengths of the sides `PQ`, `QR` and `PR` are a,b,c respectively.
Which among the following is `tanx^0`
`(a/c,b/a,a/b,b/c)`
 .
.
View SolutionIn triangle `PQR,`squareQ=90^o`, `squareR=x^o`. Lengths of the sides `PQ`, `QR` and `PR` are a,b,c respectively.
Similarly write `sin x^0` and `cos x^0` from this triangle.
 .
.
View SolutionIn triangle `PQR,`squareQ=90^o`, `squareR=x^o`. Lengths of the sides `PQ`, `QR` and `PR` are a,b,c respectively.
Prove that `(sinx^o)/(cosx^o)=tanx^o`
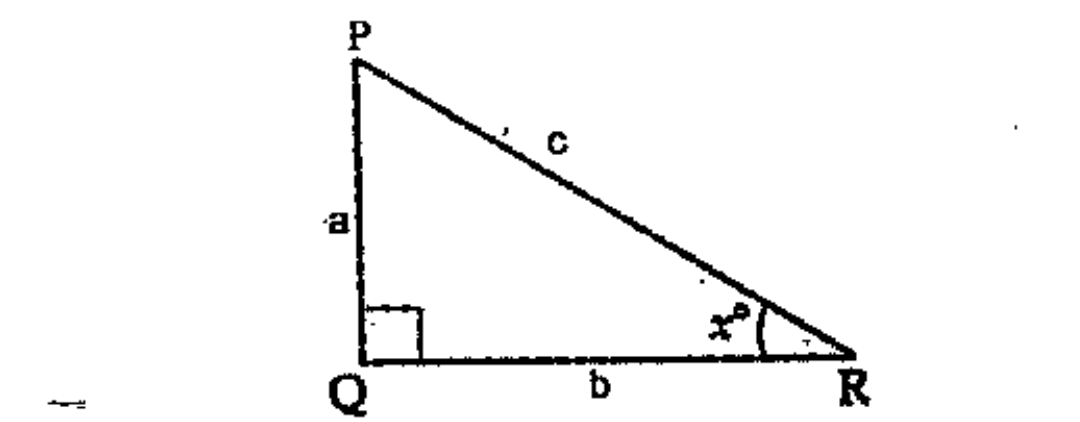 .
.
View SolutionConsider two fraction having numerator 1. The denominator of one fraction is 2 more than the denominator of the other. Sum of these fraction is `5/12` Write the above fact as an algebraic equation.
View SolutionConsider two fraction having numerator 1. The denominator of one fraction is 2 more than the denominator of the other. Sum of these fraction is `5/12`Find the fractions.
View SolutionA bag contains some red and green balls. If we take a ball from it, without looking, the probability of getting a red ball is `1/4`. What is the total number of balls, if there are 8 red balls?
View SolutionA bag contains some red and green balls. If we take a ball from it, without looking, the probability of getting a red ball is `1/4`. if there are 8 red balls,What is the probability that a ball taken is green.
View SolutionA bag contains some red and green balls. If we take a ball from it, without looking, the probability of getting a red ball is `1/4`. if there are 8 red balls, Find the sum of both the probabilities.
View SolutionFrom a box containing some red balls and some blue balls the probability of getting a red ball is `a/b`. What is the probability of getting a blue ball?.
View SolutionIn the figure, `squareP=90^o`. Sides of triangle APC are extended to B and D.
If a circle is drawn with AC as its diameter, where will be the position of P with respect to that circle?
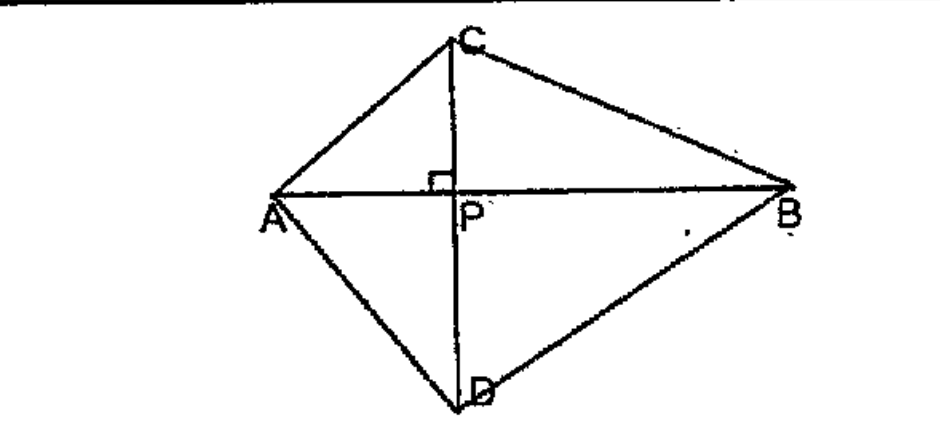 .
.
View SolutionIn the figure, `squareP=90^o`. Sides of triangle APC are extended to B and D.
What about the position of P, if the circle is drawn with AD as diameter?
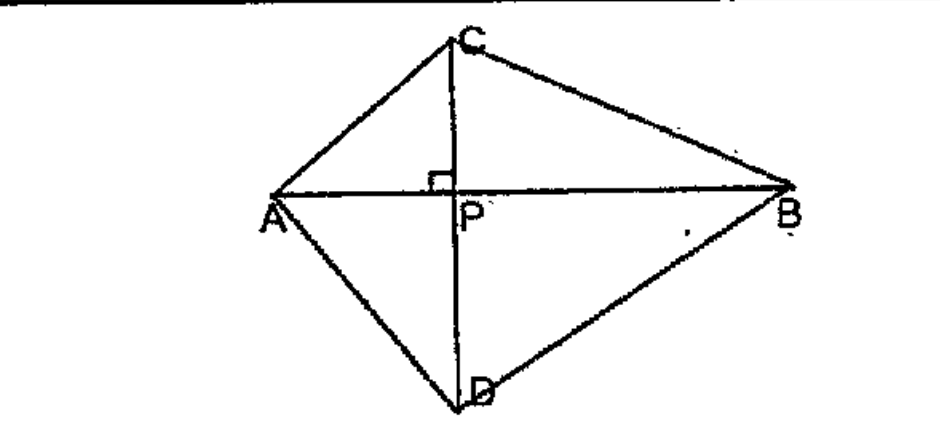 .
.
View SolutionIn the figure, `squareP=90^o`. Sides of triangle APC are extended to B and D.
Prove that, the circles drawn with the sides of a quadrilateral with perpendicular diagonals, will meet at a common point.
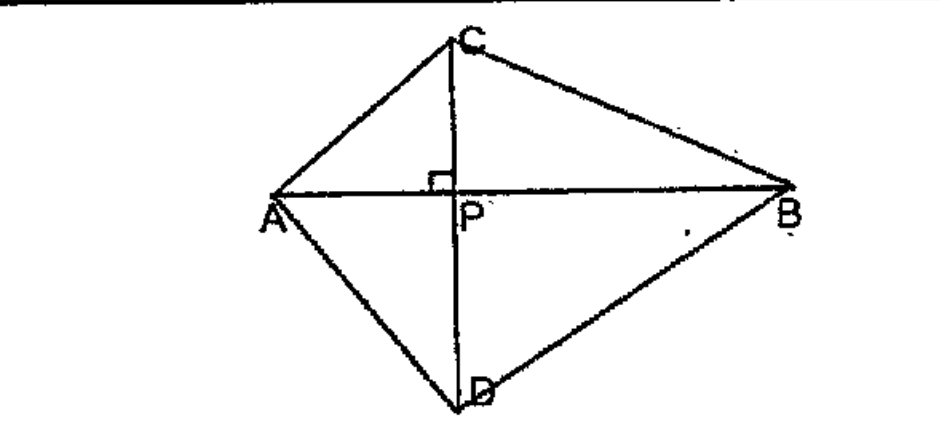 .
.
View SolutionWrite the sequence of odd numbers greater than 1.
View SolutionWrite the sequence of odd numbers greater than 1.What is the algebraic form of this sequence?
View SolutionWhat is the algebraic form of the arithmetic sequence `3/6,5/6,7/6....`.
View SolutionThe table below shows the students of a class sorted according to their scores in a test
If the students are arranged in the increasing order of their scores, the score of the student at what position is taken as the median?
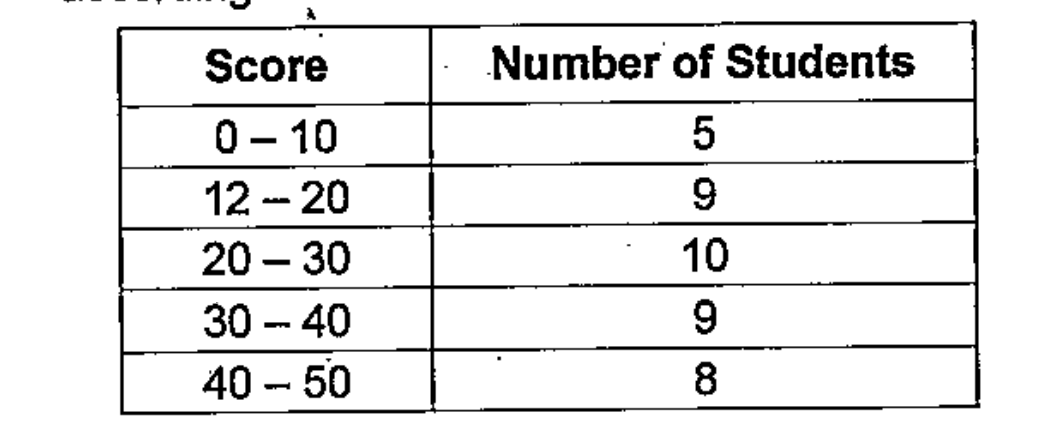 .
.
View SolutionThe table below shows the students of a class sorted according to their scores in a test
What may be assumed as the score of the `15^(th)` student in the arrangement?
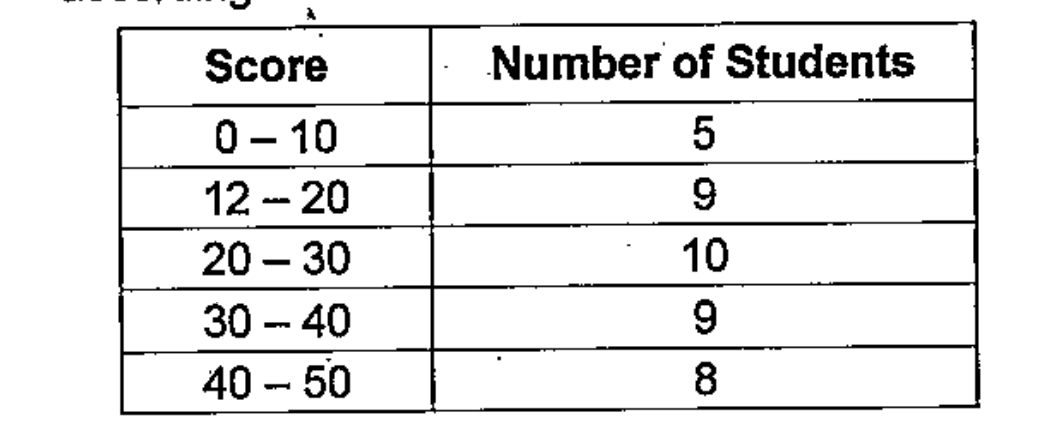 .
.
View SolutionThe table below shows the students of a class sorted according to their scores in a test
Find the median score.
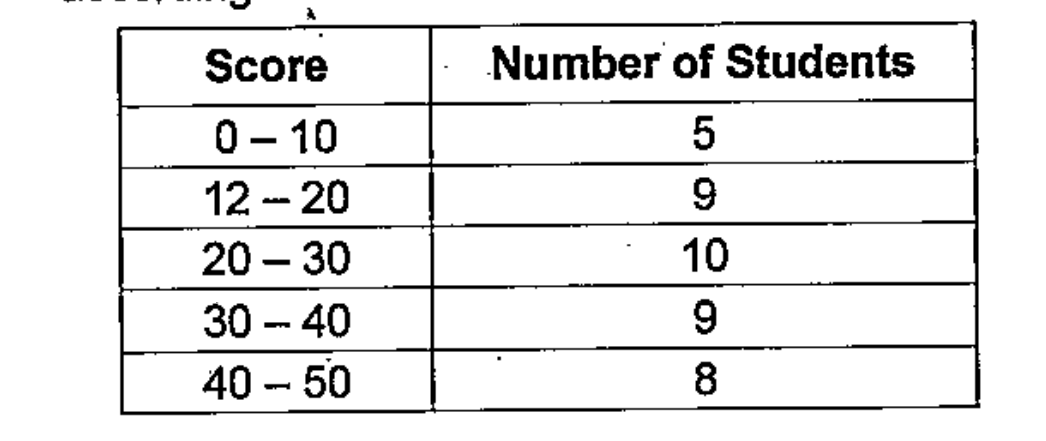 .
.
View SolutionA solid is made by fixing a hemisphere of same radius on the flat face of a cone. The height of the cone is 12 centimetres and its slant height is 13 centimetres. What is the radius of the cone?
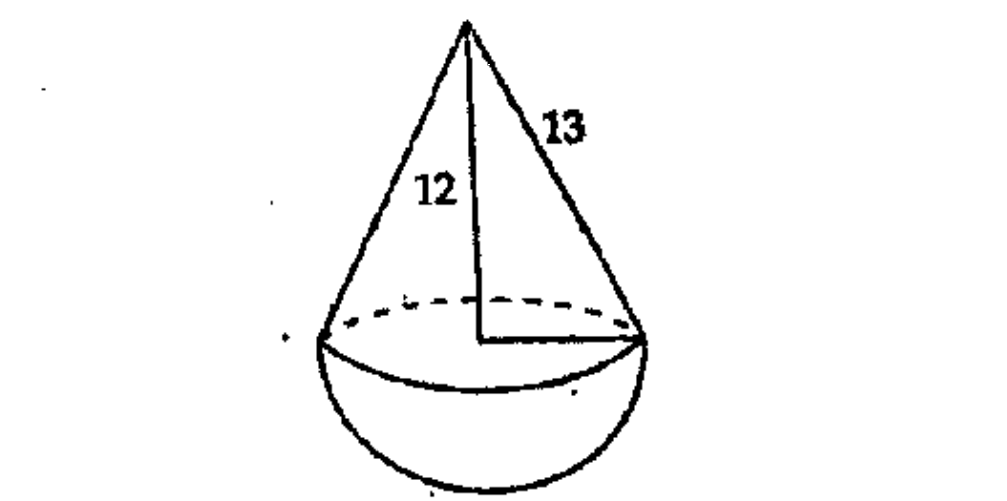 .
.
View SolutionA solid is made by fixing a hemisphere of same radius on the flat face of a cone. The height of the cone is 12 centimetres and its slant height is 13 centimetres. What is the curved surface area of the hemisphere?
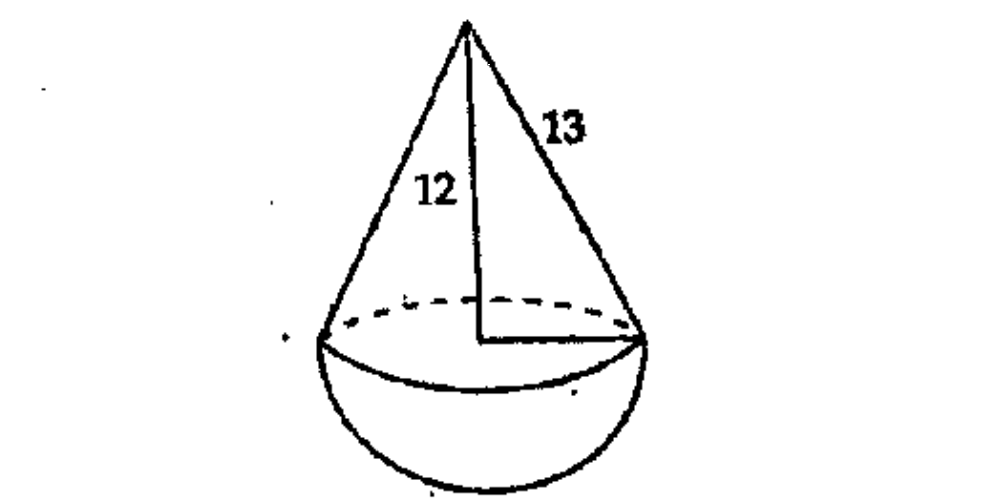 .
.
View SolutionA solid is made by fixing a hemisphere of same radius on the flat face of a cone. The height of the cone is 12 centimetres and its slant height is 13 centimetres. What is the total surface area of the solid?
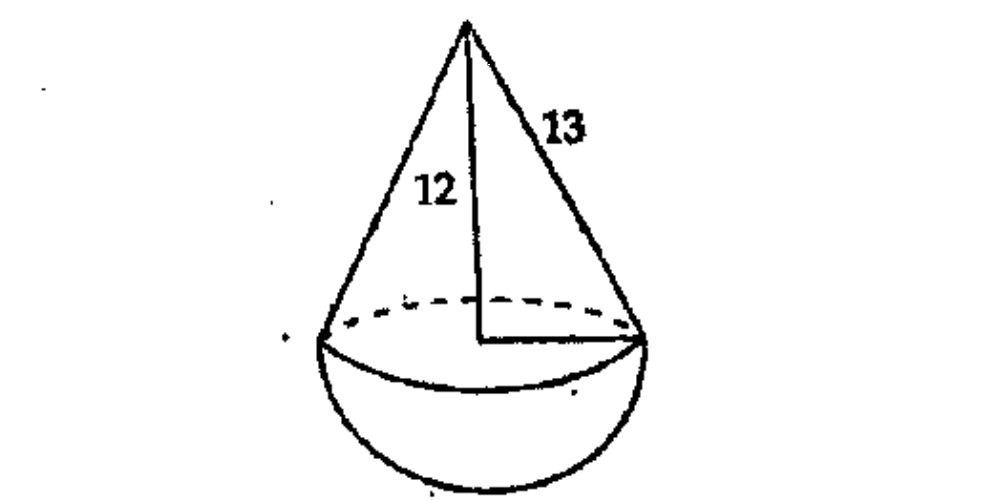 .
.
View SolutionA boy is standing between two building of equal height. The boy and the buildings are in a straight line. He see the tops of those buildings at elevations of `45^o` and `30^o`. The nearest building is 20 metres away from him. Draw a rough figure.
View SolutionA boy is standing between two building of equal height. The boy and the buildings are in a straight line. He see the tops of those buildings at elevations of `45^o` and `30^o`. The nearest building is 20 metres away from him.
Find the height of the buildings and distance between the buildings.
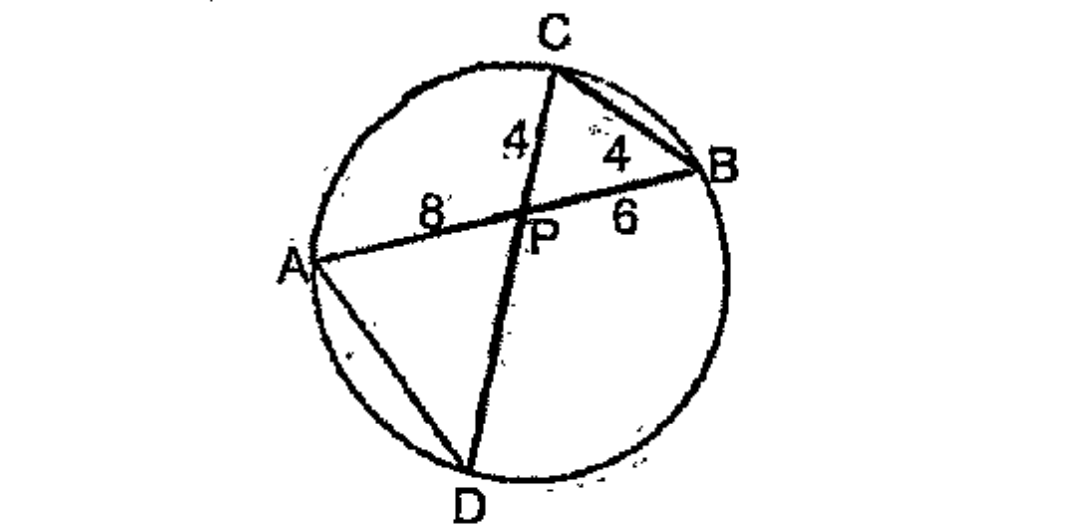
View SolutionIn the figure chords AB and CD intersect at P. `PA=8 centimetres`,`PB=6 centimetres`, `PC=4 centimetres`,`BC=4 centimetres`.
Which angle is equal to `squareA`?
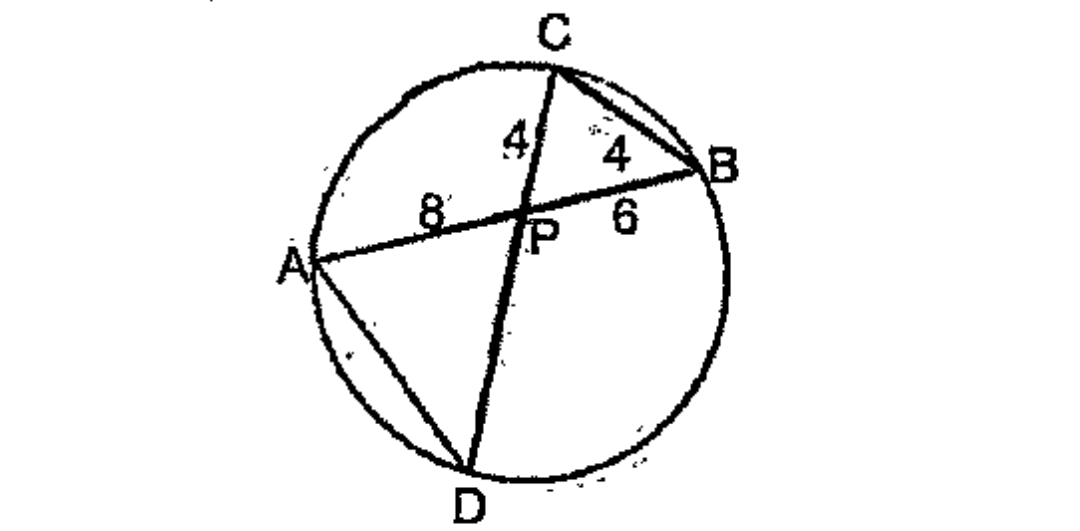 .
.
View SolutionIn the figure chords AB and CD intersect at P. `PA=8` `centimeters` ,`PB=6 centimetres`, `PC=4 centimetres`,`BC=4 centimetres`.
Write one more pair of equal angles.
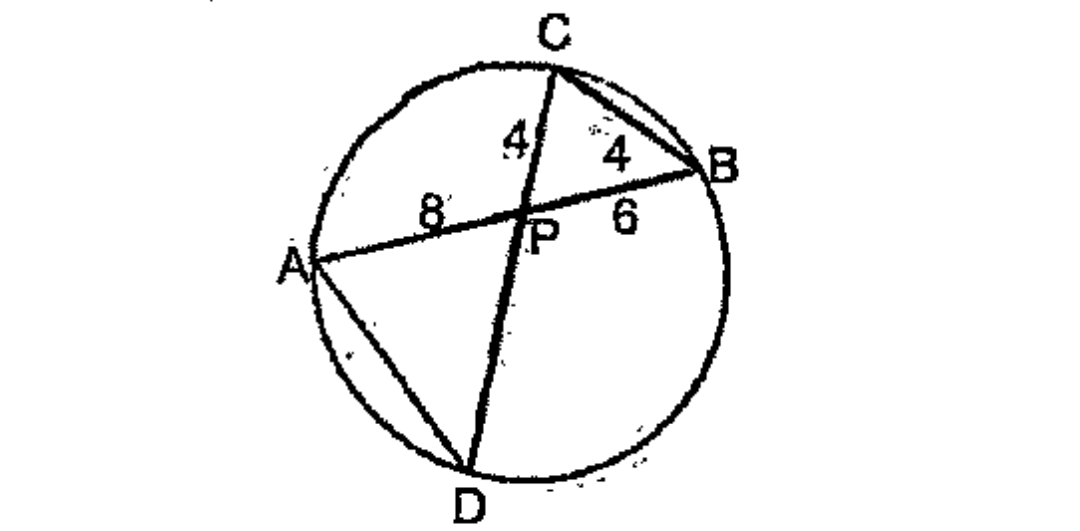 .
.
View SolutionIn the figure chords AB and CD intersect at P. `PA=8 centimetres`,`PB=6 centimetres`, `PC=4 centimetres`,`BC=4 centimetres`.
Find the length of PD.
 .
.
View SolutionThe sum of first 9 terms of an arithmetic sequence is 45 and the sum of first 18 terms is 171. What is the sum of its `10^(th)` to `18^(th)` terms?
View SolutionThe sum of first 9 terms of an arithmetic sequence is 45 and the sum of first 18 terms is 171. What is its `5^(th)` term?
View SolutionThe sum of first 9 terms of an arithmetic sequence is 45 and the sum of first 18 terms is 171. Find its `14^(th)` term.
View SolutionThe sum of first 9 terms of an arithmetic sequence is 45 and the sum of first 18 terms is 171. Find the sum of `5^(th)` to `14^(th)` terms.
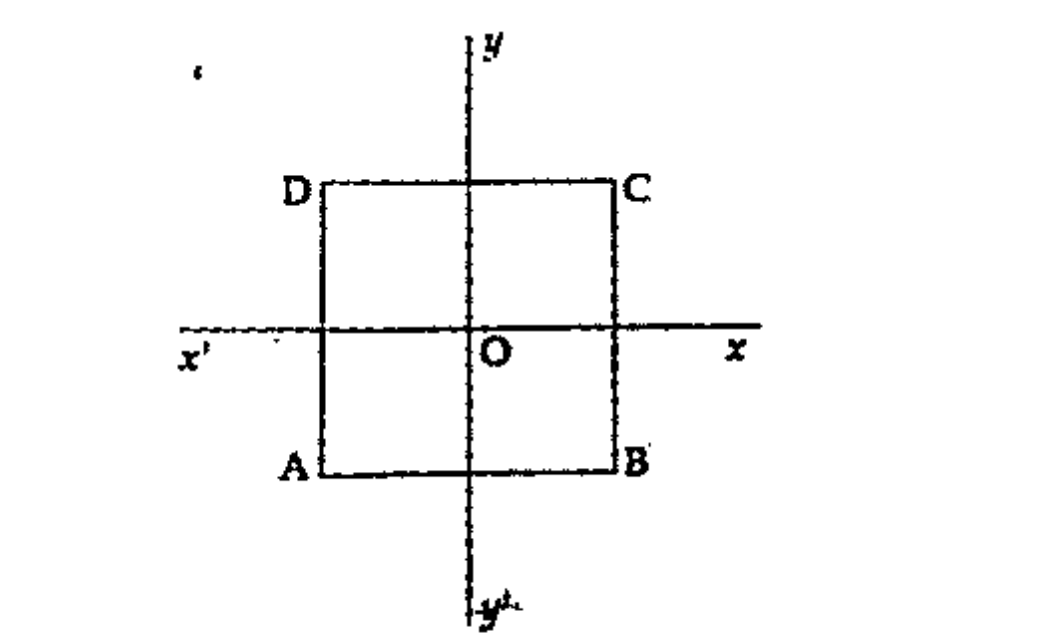
View SolutionIn this figure ABCD is a square. The axes are drawn through the mid points of its sides. The length of its side is 6 units.
Write the coordinates of its vertices.
 .
.
View SolutionIn this figure ABCD is a square. The axes are drawn through the mid points of its sides. The length of its side is 6 units.
Write the equation of its diagonal BD.
 .
.
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of `1161=The digital root of 63`, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of 345?
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of `1161=The digital root of 63`, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of 927?
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of `1161`=The digital root of `63`, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
What is the digital root of `345times927`?
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of `1161=The digital root of 63`, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
The digital root of the number `63square5` is 8 (square represents a missing digit). Find the missing digit.
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of 1161=The digital root of 63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
`121times92=11square32`. Find the missing digit.
View SolutionConsider the number 2751. The sum of its digital is `2+7+5+1=15`. Adding the digits of 15 we get `1+5=6`. This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit)
Let us see one more example.
The sum of the digits of the numbe `679412` is `6+7+9+4+1+2=29`. Sum of digits of `29=2+9=11`. Sum of digits of `11=1+1=2`. Therefore the digital root of `679412` is `2`.
Digital roots have an interesting property. To see this, consider the product `43times27=1161`. The digital roots of the numbers `43` and `27` are `4+3=7` and `2+7=9`. Product of the digital roots=`7times9=63`. Digital root of `63=6+3=9`. The Digital root of 1161 is also `9(1+1+6+1=9)` that is the digital root of `1161`=The digital root of `63`, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers.
If the digital root of `a` is 5 and the digital root of `b` is 2. Then what is the digital root of `ab`?
View Solution
EXAMPLE questions and complete solutions for chapter QUESTION PAPER FEB 2019 of MAXIMUM PUBLICATION of Class 10