Complete Solutions to EXAMPLE of chapter POLYNOMIALS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYNOMIALS |
| MBD | EXAMPLE |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
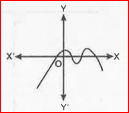
Look at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)

View SolutionLook at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)
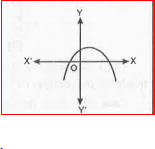
View SolutionLook at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)
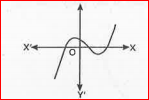
View SolutionLook at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)
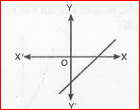
View SolutionLook at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)
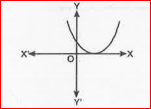
View SolutionLook at the graph in Fig. IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x)
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
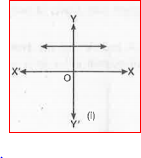 .
.
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
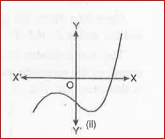 .
.
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
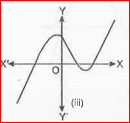 .
.
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
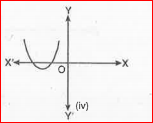 .
.
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
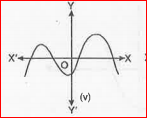 .
.
View SolutionThe graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
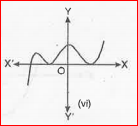 .
.
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `x^2-2x-8` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `4s^2-4s+1` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `6x^2-3-7x` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `4u^2+8u` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `t^2-15` .
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. : `3x^2-x-4` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `1/4,-1` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `sqrt2,1/3` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : `0,sqrt5` .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : 1,1
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : -1/4,1/4 .
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. : 4,1 .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^3-3x^2+5x-3, g(x)= x^2-2` .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^4-3x^2+4x+5, g(x)= x^2+1-x` .
View SolutionApply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below : `p(x)=x^4-5x+6,g(x)=2-x^2` ,
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `t^2-3,2t^4+3t^3-2t^2-9t-12` .
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `x^2+3x+1,3x^4+5x^3-7x^2+2x+2` .
View SolutionCheck whether the first polynomial is a factor of the second polynomial by applying the division algorithm : `x^3-3x+1,x^5-4x^3+x^2+3x+1` .
View SolutionObtain all other zeroes of `3x^4+6x^3-2x^2-10x-5` if two of its zeroes are `sqrt((5)/(3)` and `-sqrt((5)/(3)` .
View SolutionOn dividing `x^3-3x^2+x+2` by a polynomial g (x), the quotient and remainder were x - 2 and - 2x + 4 respectively find g (x).
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg p (x) = deg q .
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg r (x) = 0 .
View SolutionGive examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and : deg p (x) = deg q (x) .
View SolutionVerify that the number given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes . and the coefficients in each case : `2x^3+x^2-5x+2, 1/2,1,-2` .
View SolutionVerify that the number given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes . and the coefficients in each case : `x^3+4x^2+5x-2, 2,1,1` .
View SolutionFind a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, - 7, - 14 respectively.
View SolutionIf the zeroes of the polynomial `x^3-3x^2+x+1` are a -b , a, a + b, find a and b .
View SolutionIf two zeroes of the polynomial `x^4-6x^3-26x^2+138x-35` are `2+-sqrt3` , find other zeroes.
View Solution
EXAMPLE questions and complete solutions for chapter POLYNOMIALS of MBD of Class 10