Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm : t2−3,2t4+3t3−2t2−9t−12 .Solution in Punjabi
Step by step video & image solution for Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm : t^2-3,2t^4+3t^3-2t^2-9t-12 . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The graphs of y = p (x) are given in figure below, for some polynomials p (x). Find the number of zeroes of p (x), in each case.
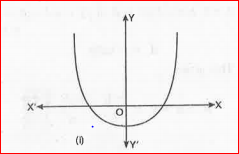 .
.
View Solution4 chairs and 3 tables cost ? 2100 and 5 chairs and 2 tables cost ? 1750. Represent this situation algebraically and graphically.
View SolutionIf a die is thrown, what is the probability that an 'ace' turns up ?
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :t2−3,2t4+3t3−2t2−9t−12
View SolutionCheck whether g(t)=t2−3 is a factor of f(t)=2t4+3t3−2t2−9t−12 by applying the division algorithm.
View Solutionपहले बहुपद से दूसरे बहुपद को भाग करके, जॉंच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है :
g(t)=t2−3,f(t)=2t4+3t3−2t2−9t−12
View SolutionCheck in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
(i) t2−3,2t4+3t3−2t2−9t−12.
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing :
t2−3,2t4+3t3−2t2−9t−12
View Solution(i) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
t2−3,2t4+3t3−2t2−9t−12
(ii) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial
x2+3x+1,3x4+5x3−7x2+2x+2
(iii) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
x3−3x+1,x5−4x3+x2+3x+1
View SolutionDivide the second polynomial by the first polynomial and check whether the first polynomial is a factor of the second polynomial. t^2 - 3, 2t^4 + 3t^3 - 2t^2 - 9t - 12
View Solutionకింది బహుపదులలో రెండవ బహుపదిని , మొదటి బహుపదిచే భాగించి ప్రతి సందర్భంలో మొదటి బాహుపది కారణాంకం అగునో, కాదో సరిచూడండి. t2−3,2t4+3t3−2t2−9t−12
View SolutionCheck in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
t2−3,2t4+3t3−2t2−9t−12
View SolutionCheck in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
t2−3,2t4+3t3−2t2−9t−12
View SolutionCheck in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
t2−3,2t4+3t3−2t2−9t−12
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) x2+3x+1,3x4+5x3−7x2+2x+2
(ii) t2−3,2t4+3t3−2t2−9t−12
View Solution
