Complete Solutions to EXAMPLE of chapter INTRODUCTION TO TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | INTRODUCTION TO TRIGONOMETRY |
| MBD | EXAMPLE |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
In `triangleABC`, right angled at B, AB = 24 cm ,BC = 7 cm. Determine :- sinA, cosA.
View SolutionIn `triangleABC`, right angled at B, AB = 24 cm ,BC = 7 cm. Determine :- sinC, cosC.
View SolutionIn fig., find tan P - cot R.
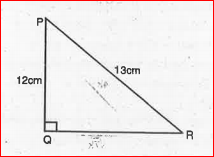
View SolutionIf sin A = `3/4` calculate cos A and tanA.
View SolutionGiven 15 cot A = 8, find sin A and sec A.
View SolutionGiven sec = `13/2` , calculate all other trigonometric ratios.
View Solutionif `angleA` and `angleB` are acute angles such that cos A = cos B , show that `angleA=angleB` .
View SolutionIf `cottheta=7/8` evaluate :- `((1+sintheta)(1-sintheta))/((1+costheta)(1-costheta)` .
View SolutionIf `cottheta=7/8` evaluate :- `cot^2theta` .
View SolutionIf 3cotA=4, check whether 1-tan ^2 A/ 1+tan ^2 A =cos ^2 A−sin ^2 A or not
View SolutionIn triangle ABC, right angled at B, if tan A = `1/sqrt3` . Find the value of :- sin A cos C + cos A sin C.
View SolutionIn triangle ABC, right angled at B, if tan A = `1/sqrt3` . Find the value of :- cos A cos C -sin A sin C.
View SolutionIn `trianglePQR`, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
View SolutionState whether the following are true or false. Justify your answer. :- The value of tan A is always less than 1.
View SolutionState whether the following are true or false. Justify your answer. :- sec A = `12/5` for some value of angle A.
View SolutionState whether the following are true or false. Justify your answer. :- cos A is abbreviation used for cosecant of angle A.
View SolutionState whether the following are true or false. Justify your answer. :- cot A is product of cot and A.
View SolutionState whether the following are true or false. Justify your answer. :-`sin=4/3` for some angle `theta` .
View SolutionChoose the correct option and justify your choice.:- `(2tan30^@)/(1+tan^2 30^@)`.
View SolutionChoose the correct option and justify your choice.:- `(1-tan^2 45^@)/(1-tan 45^@)`
View SolutionChoose the correct option and justify your choice.:- sin 2A = 2 sin A is true when A
View SolutionChoose the correct option and justify your choice.:- `(2tan30^@)/(1-tan^2 30^@)` .
View SolutionIf tan(A+B)=`sqrt3` and tan(A-B)=`1/sqrt3` , `0^@angleA+Ble90^@` , A>B, find A and B .
View SolutionState whetherthe following are true or false. Justify your answer. :- sin (A+B)=sinA+sinB.
View SolutionState whetherthe following are true or false. Justify your answer. :- The value of sin q increases as q increases.
View SolutionState whetherthe following are true or false. Justify your answer. :- The value of cos q increases as q increases.
View SolutionState whetherthe following are true or false. Justify your answer. :- sin q = cos q for all value of q.
View SolutionState whetherthe following are true or false. Justify your answer. :- cot A is not defined for A =`0^@` .
View SolutionEvaluate : `(sin18^@)/(cos72^@)` .
View SolutionEvaluate : `(tan26^@)/(cot64^@)` .
View SolutionEvaluate : `cos48^@-sin42^@` .
View SolutionEvaluate : `co s e c31^@-sec59^@` .
View SolutionShow that : `tan48^@tan23^@tan42^@tan67^@=1` .
View SolutionShow that : `cos38^@cos52^@-sin38^@sin52^@=0` .
View SolutionIf tan 2A = cot (A - `18^@`) where 2A is an acute angle, find the value of A.
View SolutionIf tan A = cot B, prove that A + B = `90^@` .
View SolutionIf sec 4A = cosec (A -`20^@`), where 4A is an acute angle, find the value of A.
View SolutionIf A, B and C interior angles of a triangle ABC, then show that : `sin((B+C)/2)=cos(A/2)` .
View SolutionExpresssin `67^@` + cos `75^@` in terms of Trigonometric ratios of angles between `0^@` and `45^@`.
View SolutionExpress the trigonometric ratios of sin A, sec A and tan A in terms of cot A.
View SolutionWrite all the other trigonometric ratios of `angle`A in terms of sec A.
View SolutionEvaluate :- `(sin^2 63^@+sin^2 27^@)/(cos^2 17^@+cos^2 73^@)` .
View SolutionEvaluate :- `sin25^@cos65^@+cos25^@sin65^@` .
View SolutionChoose the correct option. Justify your choice : `9sec^2A-9tan^2A=` a. 1 b. 9 c. 8 d. 0
View SolutionChoose the correct option. Justify your choice : `(1+tantheta+sectheta)(1+cottheta-cosectheta)`
View SolutionChoose the correct option. Justify your choice : (sec A + tan A) (1-sin A) = ? a. sec A b. sin A c. cosec A d. cos A
View SolutionChoose the correct option. Justify your choice : `(1+tan^2A)/(1+cot^2A)` a. `sec^2A` b. -1 c. `cot^2A` d. `tan^2A`
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosectheta-cottheta)^2=(1-costheta)/(1+costheta)` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosA)/(1+sinA)+(1+sinA)/(cosA)=2secA` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(tantheta)/(1-cottheta)+(cottheta)/(1-tantheta)=1+secthetacosectheta` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(1+secA)/(secA)=(sin^2A)/(1-cosA)` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosA-sinA+1)/(cosA+sinA-1)=cosecA+cotA,` using the identity `coses^2A=1+cot^2A)`
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `sqrt((1+sinA)/(1-sinA))=secA+tanA` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(sintheta-2sin^3theta)/(2cos^3theta-costheta) =tantheta` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(sin A + cosec A)^2+(cosA+secA)^2=7+tan^2A+cot^2A` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : (cosec A -sin A) (sec A - cos A) = sin A.cos A
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `((1+tan^2A)/(1+cot^2A))=((1-tanA)/(1-cotA))^2=tan^2A` .
View SolutionThe hypotenuse is the……….. Side in right triangle.
View SolutionThe value of tan A can not be greater than 1.
View Solution`sin^2theta+cos^2theta=1` .
View SolutionValue of tan A is always less than 1.
View Solution`cos(90^@-theta)=sintheta` .
View Solutionsin (A + B) = sin A + sin B.
View Solution`sin30^@`= …………….. .
View Solution`cos30^@`= ……….. .
View Solution…………….. - `cot^2 theta`=1 . Fill the blank.
View Solution`sin^2theta`+……………… = 1 . Fill in the blank.
View Solution`sec^2theta` - ……….. = 1 . Fill in the blank.
View SolutionEvaluate : `cosec59^@-sec31^@` .
View SolutionEvaluate : `cos48^@-sin42^@` .
View SolutionEvaluate : `tan59^@-cot31^@` .
View SolutionWhat is the value of `(sin16^@)/(cos74^@)` .
View SolutionWhat is the value of `(sin18^@)/(cos72^@)` .
View SolutionWhat is the value of `(sin14^@)/(cos76^@)` .
View SolutionIf tanA=cotB, prove that A+B=`90^@` .
View SolutionEvaluate : `tan65^@/cot25^@` .
View Solution
EXAMPLE questions and complete solutions for chapter INTRODUCTION TO TRIGONOMETRY of MBD of Class 10