Complete Solutions to EXERCISE of chapter INTRODUCTION TO TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | INTRODUCTION TO TRIGONOMETRY |
| MBD | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In `triangleABC`, right angled at A, if AB = 12 cm, AC = 5 cm and BC = 13 cm, find all the six trigonometric ratios of angle B.
View SolutionIn `triangleOPQ`, right angled at P, OP = 7 cm and OQ - PQ = 1 cm. Determine the values of sin `theta` and cos `theta`.
View SolutionIf `sintheta=sqrt3costheta` , find all the six T-ratios..
View SolutionIf sin A = `1/3` evaluate the cos A cosec A + tan A sec A.
View SolutionIf tan`theta=12/5`, calculate sin`theta` , cos`theta` and verify `sin^2theta+cos^2theta` .
View SolutionIf tan A = `sqrt2-1` show that `(tanA)/(1+tan^2A)=(sqrt2)/4` = sinA cos A .
View SolutionIf sec `theta=5/4` verify that `(tantheta)/(1+tan^2theta)=(sintheta)/(sectheta)` .
View SolutionIf sin B=`1/2` find the value of 3 cosB-`4cos^3B` .
View SolutionIn a right angled triangle ABC, right angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
View SolutionIf `cottheta=3/4` prove that `sqrt((sectheta-cosectheta)/(sectheta+cosectheta))=1/sqrt7` .
View SolutionIf tan `theta=3/4` , show that `sqrt((1-sintheta)/(1+sintheta))=1/2` .
View SolutionIn `triangleABC` , right angle at C, if tan A =`1/sqrt3`. Show that sin A cos B -cos A sin B =`- 1/2` .
View SolutionIf cosec A = 2 , find the value of `1/(tan A)+(sinA)/(1+cosA)`.
View SolutionIf cot B=`12/5` Prove that `tan^2B-sin^2B=sin^4B.sec^2B` .
View SolutionIf `tantheta+(1)/(tantheta)=2` , find the value of `tan^2theta+(1)/(tan^2theta` .
View SolutionIf 3`cos theta-4sintheta=2costheta+sintheta` find `tantheta` .
View SolutionIf `sintheta=3/5`, evaluate `[(costheta-(1/tantheta))/(2cottheta)]` .
View SolutionWhat is the value of `sina` .
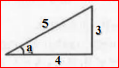 .
.
View SolutionIf A=`30^@` verify that :- cos2A= `(1-tan^2A)/(1+tan^2A)` .
View SolutionIf A=`30^@` verify that :- cos2A= `cos^2A-sin^2A` .
View SolutionIf A=`30^@` verify that :- cos2A=1-`2sin^2A` .
View SolutionIf A=`30^@` verify that :- cos2A= 2`cos^2`A-1 .
View SolutionIf A=`30^@` verify that :- sin3A=3sinA-`4sin^3` A .
View SolutionIf A=`30^@` verify that :- cos3A=4`cos^3 A`-3cosA .
View SolutionIf A=`30^@` verify that :- tanA= `sqrt((1-cos^2A)/cos^2A` .
View SolutionIf A=`30^@` verify that :- sinA=tanA/ `sqrt(1+tan^2A)` .
View SolutionEvaluate :- `2sin^2 60^@+cot^2 30^@-tan 45^@` .
View SolutionEvaluate :- `(5sin^2 30^@+cos^2 45^@+4tan^2 45^@)/(2sin30^@ cos60^@+tan45^@)` .
View SolutionEvaluate :- `tan60^@/(sec60^@+cosec60^@)` .
View SolutionEvaluate :- `sin^2 30^@ cos^2 45^@+4tan^2 30^@+1/2sin^2 90^@+1/8cot^2 90^@` .
View SolutionIf sin (A + B) = 1 and cos (A -B) = `sqrt3/2` .Find A and B.
View SolutionIf sin (A-B)=`1/2` , cos(A+B)=`1/2` . Find A and B.
View SolutionIf cos (A+B)=0 and sin(A-B) = `1/2` . Find A and B .
View SolutionIf 3`tan2theta=sqrt3` find `theta` .
View SolutionFind x , if 2`cosec^2 30^@+xsin^2 60^@-3/4 tan^2 30^@` = 10 .
View SolutionGiven that cos (A + B) = cos A cos B-sin A sin B. Find the value of cos `105^@`.
View SolutionFind x if :- `cos(10^@+x)=1/2` .
View SolutionFind x if :- `tan(40^@+x)=sqrt3` .
View SolutionFind x if :- `sin(20^@+x)=cos60^@` .
View SolutionFind x if :- if cos (40+x)=`sin30^@`. Find the value of x.
View SolutionShow that :- `2[cos^4 60^@+sin^4 30^@]-[tan^2 60^@+cot^2 45^@]+3sec^2 30^@=1/4` .
View SolutionShow that :- `2[cos^2 45^@+tan^2 60^@]-6[sin^2 45^@-tan^2 30^@]=6` .
View SolutionFind the value `theta` in the following :- `2sin2theta=sqrt3` .
View SolutionFind the value `theta` in the following :- `2cos3theta=1` .
View SolutionFind the value `theta` in the following :- `sqrt3 tan2theta-3=0` .
View SolutionFind the value `theta` in the following :- `tan3theta=sin45^@ cos45^@+sin30^@` .
View SolutionFind the value `theta` in the following :- `costheta=cos60^@ cos30^@ +sin60^@ sin30^@ ` .
View SolutionFind the value `theta` in the following :- `sin2theta=sin60^@cos30^@-cos60^@sin30^@` .
View SolutionIfsin(A-B)= sin A cosB-cos A sin B and cos(A-B) = cosA cosB + sin A sin B. Find the values of sin `15^@` and cos`15^@` .
View SolutionExpress cot `85^@` + `cos 75^@` in terms of trigonometric ratios of angles between `0^@` and `45^@`.
View SolutionWithout using Trigonometric tables, evaluate:- `2(sin43^@)/(cos47^@)-(cot30^@)/(tan60^@)-sqrt2 sin45^@` .
View SolutionWithout using Trigonometric tables, evaluate:- `(cos^2 20^@+cos^2 70^@)/(sin^2 59^@+sin^2 31^@)` .
View SolutionWithout using Trigonometric tables, evaluate:- `2(cos67^@)/(sin23^@)-(tan 40^@)/(cot50^@)-sin90^@` .
View SolutionEvaluate : `(sin70^@)/(cos 20^@)+(cosec36^@)/(sec54^@)-(2cos43^@cosec47^@)/(tan10^@tan40^@tan50^@tan80^@` .
View SolutionEvaluate : `(tan20^@)/(cot70^@) +(cot50^@)/(tan40^@)+(sin^2 20^@+sin^2 70^@)/(sinthetacos(90-theta)+costhetasin(90-theta)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `sinthetacostheta-(sinthetacos(90^@-theta) costheta)/(sec(90^@-theta))-(costhetasin(90^@-theta)sintheta)/(cosec(90^@-theta))` .
View SolutionEvaluate : `tan 15^@ tan25^@tan60^@tan65^@tan75^@` .
View SolutionEvaluate : `tan65^@/cot25^@` .
View SolutionIf sin 3A = cos (A- `26^@`) where 3A is an acute angle, find the value of A.
View SolutionEvaluate : `(cos80^@)/(sin10^@)+cos59^@ cosec31^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `sec70^@sin20^@-cos20^@cosec70^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(2cos38^@)/(sin52^@)+(4tan40^@)/(cot50^@)+(12sec66^@)/(cosec24^@)`
View SolutionWithout using Trigonometric Tables evaluate the following :- `(cosec^2 67^@-tan^2 23^@)/(sin^2 17^@+sin^2 73^@)+(sin59^@)/(cos31^@)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(cos35^@)/(sin55)+(sin11^@)/(cos79^@)-cos28^@ cosec62^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(cos58^@)/(sin32^@)+(sin22^@)/(cos68^@)-(cos38^@ cosec52^@)/(tan18^@tan35^@tan60^@tan72^@tan55^@)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `((tan20^@)/(cosec70^@))^2+((cot20^@)/sec70^@)+2tan15^@tan37^@tan53^@tan60^@tan75^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `3((sin36^@)/(cos54^@))^2 -2((tan18^@)/cot72^@)^3+2tan13^@tan21^@tan69^@tan77^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(tan 48)/(2cot42^@)+(3cosec31^@)/(sec59^@)-(cos69^@)/(2sin21^@)+2tan23^@tan37^@tan67^@tan53^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `sinthetacostheta-(sinthetacos(90^@-theta) costheta)/(sec(90^@-theta))-(costhetasin(90^@-theta)sintheta)/(cosec(90^@-theta))` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(2cos67^@)/(sin23^@)-(tan40^@)/(cot50^@)-cos0^@+tan15^@tan25^@tan60^@tan65^@tan75^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(2cos65^@)/(sin25^@)-(tan20^@)/(cot70^@)-sin90^@+tan5^@tan35^@tan60^@tan55^@tan85^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `2[(cos^2 20^@+cos^2 70^@)/(sin^2 25^@+sin^2 65^@)]-tan45^@+tan13^@tan23^@tan30^@tan67^@tan77^ @`
View SolutionWithout using Trigonometric Tables evaluate the following :-
`(sec50^@sin40^@+cos40^@cosec50^@)`
View SolutionWithout using Trigonometric Tables evaluate the following :- `(1/2sec^2 60^@-1/2tan^2 60^@)/(4[cos^2 29^@+cos^2 61^@]` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(2sin68^@)/(cos22^@)-(2cot15^@)/(5tan75^@)-(3tan45^@tan20^@tan40^@tan70^@tan50^@)/5` .
View SolutionEvaluate : `(sin70^@)/(cos 20^@)+(cosec36^@)/(sec54^@)-(2cos43^@cosec47^@)/(tan10^@tan40^@tan50^@tan80^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(sin^2 35^@+sin^2 55^@)/(tan10^@tan20^@tan30^@tan70^@tan80^@)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(sin^2 35^@+sin^2 55^@)/(tan10^@tan20^@tan30^@tan70^@tan80^@)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(sec^2 54^@-cot^2 36^@)/(cosec^2 57^@-tan^2 33^@) +2sin^2 38^@ sec^2 52^@-sin^2 45^@` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `sec^2 10^@-cot^2 80^@+(sin15^@cos75^@+cos15^@sin75^@)/(costhetasin(90^@-theta)+sinthetacos(90^@-theta)` .
View SolutionWithout using Trigonometric Tables evaluate the following :- `(sec^2(90^@-theta)-cot^2theta)/(2[sin^2 25^@+sin^2 65^@]) +(2cos^2 60^@tan^2 28^@tan^2 62^@)/(3[sec^2 43^@-cot^2 47^@]` .
View SolutionIf sin 3`theta` = cos `(theta-6^@)` where 3`theta` and `theta-6^@` are acute angles, find the value of `theta` .
View SolutionIf sin A = cos B, both A and B are acute angles, find A + B.
View SolutionIf cosec 2A = sec (A + `6^@`) where 2A and A + `6^@` are acute angles find the value of A.
View SolutionIf sin 5`theta` = cos 4`theta` where 5`theta` and 4`theta` are acute angles, find the value of `theta`.
View SolutionIf tan 2`theta` = cot 4`theta` where 2`theta` and 4`theta` are acute angles. Find `theta`
View SolutionIf cos 3`theta`= sin (`theta` - `6^@`) where 3`theta` and `theta`-`6^@` are acute angles, find the value of `theta`.
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `sin((A+C)/2)=cos (B/2)` .
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `cos((B+C)/2)=sin(A/2)` .
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `cos^2(A/2)+cos^2((B+C)/2)=1` .
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `1+tan^2((B+C)/2)=cosec^2A/2` .
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `1+cot^2((B+C)/2)=sec^2 "A/2` .
View SolutionIf A, B, C are interior angles of `triangle`ABC, prove that :- `tan((A+B)/2)=cot "C/2` .
View SolutionMatch the following :
 .
.
View SolutionProve that sec A (1 -sin A) (sec A + tan A) =1.
View SolutionProve the following : `(cot A - cos A)/(cot A + cos A)`= `(cosec A -1)/(cosec A + 1)` .
View SolutionProve the following : `(sintheta-costheta+1)/(sintheta+costheta-1)=(1)/(sectheta-tantheta)` .
View SolutionProve the following : `tan^2A-tan^2B=(sin^2A-sin^2B)/(cos^2Acos^2B)` .
View Solution(sec A - cos A) (cot A + tan A) = tan A sec A.
View Solutionsin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A .
View Solution
EXERCISE questions and complete solutions for chapter INTRODUCTION TO TRIGONOMETRY of MBD of Class 10