Complete Solutions to Exercise of chapter Circles of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | Circles |
| MBD | Exercise |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Fill in blanks-
A secant drawn to a circle intersect the circle in ____points.
View SolutionFill in blanks-
From a point outside a circle exactly ___tangents can be drawn to the circle.
View SolutionFill in blanks-
The tangent at any point of a circle is ______to the radius through the point of contact.
View SolutionA point P is 25 cm from the center of a circle. The radius of the circle is 7 cm and length of the tangent drawn from P to the circle is :
View SolutionA point P is 20 cm from the center of a circle.The radius of the circle is 12cmand length of the tangent drawn from P to the circle is:
View SolutionA tangent PQ at a point P of a circle of radius 7 m meets a line through the center O at a point Q so that OQ = 11 m. Length PQis:
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
View SolutionIn Fig., if TP and TQ and two tangents to a circle with centre O so that ZPOQ = `110^@`, then ZPTQ is equal to
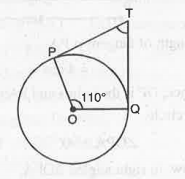
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of `80^@`, then `angle`POA is equal to
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
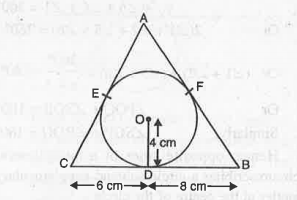
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact Dare of lengths 8 cm and 6 cm respectively (see Fig). Find the sides AB and AC.
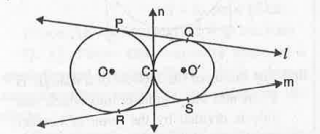
View SolutionIn the figure, two circles touch each other externally at C. Prove that the common tangent at C bisects the other two common tangents.
View SolutionIf a rectangle be circumscribed about a circle prove that it is a square.
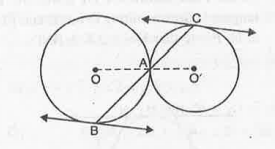
View SolutionIn fig., two circles with centres O, O' touch externally at a point A. A line through A is drawn to intersect these circles in B and C. Prove that the tangents at B and C are parallel.
View SolutionTwo circles touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ = TR
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that `angle PTQ=2angleOPQ`.
View Solution
Exercise questions and complete solutions for chapter Circles of MBD of Class 10