Complete Solutions to Example of chapter Surface Areas And Volumes of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | Surface Areas And Volumes |
| MBD | Example |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
2 cubes each of volume 64 `cm^3` are joined end to end. Find the surface area of the resulting cuboid.
View SolutionA vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
View SolutionA toy isin the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
View SolutionA cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have ? Find the surface area of the solid.
View SolutionA hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
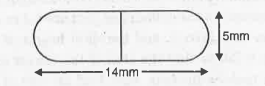
View SolutionA medicine capsule isin the shape of a cylinder with twohemispheresstuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
View SolutionA tent is in the shape of a cylinder surmounted by a conical top.If the height and diameter of the cylindrical part are 2.1m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per `m^2` (Note that the base of the tent will not be covered with canvas.)
View SolutionFrom a solid cylinder whose height is 2.4 cm and diameter 1.4cm,aconical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest `cm^2`.
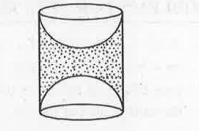
View SolutionA wooden article was made by scooping out a hemisphere form each end of a solid cylinder, as shown in Fig. If the height of the cylinder is 10cm and its base radius 3.5cm find the total surface area of the article.
View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of cylinder of radius 6 cm. Find the height of the cylinder.
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View SolutionA 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form platform of 22 m by 14 m. Find the height of the platform.
View SolutionA well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and hight 15 cm isfull of ice-cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionHow many silver coins 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions `5.5 cm xx 10 cm xx 3.5 cm` ?
View SolutionA cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
View SolutionWater in a canal 6 m wide and 1.5 m deep is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed ?
View SolutionA farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2m deep.If water flowsthrough the pipe at the rate of 3 km/h, in how much time will the tank be filled ?
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
View SolutionThe slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
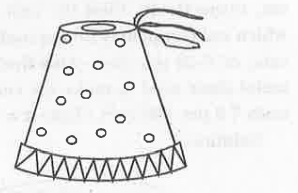
View SolutionA fez, the cap used by the Turks, is shaped like the frustum of a cone.If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
View SolutionA container opened from the top is made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate, of Rs 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs 8 per 100 `cm^2`. (Take `pi` = 3.14.)
View SolutionA cylindrical road-roller made of iron is 1 m long. Its internal diameter is 54 cm and the thikcness of the iron sheet used in making the rolleris 9cm. Find the mass of the roller, if 1 `cm^3` iron has 7.8 g mass. (Use `pi` = 3.14)
View SolutionIf the radii of the ends of a buckets 45 cm high are 28 cm and 7 cm , determine its capacity and surface area.
View SolutionThe height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/27` of the volume of the given cone, at what height above the base is the session made?
View SolutionThe height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/64` of the volume of given cone, at what height above the base is the section made?
View SolutionIf the radii of the ends of a bucket 54 cm high are 28 cm and 14 cm, determine its capacity and the surface area.
View SolutionA right circular cone is cut by two planes parallel to the base and trisecting the height. Compare the volumes of three parts into which the cone is divided.
View SolutionA solid cone of base radius t 10 cm is to be cut into two parts through the mid point of its height , by a plane parallel to the base. Find the ratio in the volume of two parts of the cone
View SolutionA lampshade is made by cutting the top of a hollow cone by a plane parallel to its base. The radii of the top and the base of the shade are 4 cm and 12 cm and the height of the shade is 6 cm. Find the area of the curved surface of the lampshade.
View SolutionThe perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm , find its volume, the slant surface and the total surface
View SolutionA container made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the metal sheet used, if it costs Rs 5 per 100 cm2.
View SolutionA copper wire 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm,so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to 8.88 g per `cm^3`.
View SolutionA right triangle, whose sides are 3cm and 4cm (other than hypotenuse)ismade to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of `pi` as found appropriate.)
View SolutionA cistern, internally measuring `150 cm xx 120 cm xx 110 cm`, has 129600 `cm^3` of water in it. Porous bricks are placed in the water until the cistern isfull to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without the water overflowing, each brick being `22.5 cm xx 7.5 cm xx 6.5 cm` ?
View SolutionIn one for night of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 97280 `km^2`, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
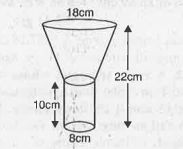
View SolutionAn oil funnel made of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel.
View SolutionDerive the formula for the curved surface area and total surface area of a frustum of acone, given to youinSection 13.5, using the symbols as explained.
View SolutionWrite the formula for volume of the frustum of the Cone
View SolutionThe formula for finding the surface area of the sphere is `frac(4)(3)pi^3`
View SolutionWrite the formula for volume of the frustum of the Cone
View SolutionWrite the formula to find the curved surface area of a cone
View SolutionFind the volume of a cube with edge 6 cm
View SolutionFind the volume of a cube with edge 8 cm.
View SolutionWrite the formula to find volume of a cylinder with radius 'r' and height ‘h'.
View SolutionWrite the formula to find and volume of a cone with radius 'r' and height 'h'.
View SolutionWrite the formula to find the curved surface area of a cylinder with radius ‘r' and height ‘h'.
View SolutionFind the volume of sphere whose radius is 3 cm
View SolutionFind the volume of sphere whose radius is 21 cm
View SolutionFind the surface area of sphere whose radius is 3 cm.
View SolutionThe length, breadth and height of the hall is 14m, 9m and 7m respectively. Find the area of the floor
View SolutionThe length, breadth and height of the hall is 15 m, 9 m and 7 m respectively. Find the area of the floor.
View SolutionThe length, breadth and height of the hall is 16 m, 9 m and 7 m respectively. Find the area of the floor.
View SolutionWrite the formula to find the volume of cuboid.
View Solution
Example questions and complete solutions for chapter Surface Areas And Volumes of MBD of Class 10