Complete Solutions to Excercise of chapter Surface Areas And Volumes of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | Surface Areas And Volumes |
| MBD | Excercise |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm. Find the surface area of the toy
View SolutionA solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere and total height of the toy, if height of the cone is three times the radius.
View SolutionAn underground water tank is in the form of a cuboid of edges 48 m, 36 m and 28 m. Find the volume of the tank.
View SolutionThe volume of a cube is `1728 cm^3`. Find its edge and surface area.
View SolutionThe diameter of the base of a right circular cylinder is 28 cm and its height is 21 cm. Find its curved surface area
View SolutionThe diameter of the base of a right circular cylinder is 28 cm and its height is 21 cm. Find its total surface area
View SolutionThe diameter of the base of a right circular cylinder is 28 cm and its height is 21 cm. Find its volume.
View SolutionThe curved surface area of a right circular cone is 12320 `cm^2`. If the radius of its base is 56 cm, find its height.
View SolutionFind the volume and the surface area of a metallic sphere having diameter 8.4 cm
View SolutionThe internal and external diameters of a hollow hemisphere vessel are 42 cm and 45.5 cm respectively. Find its capacity and also its outer curved surface area.
View SolutionThe radius of a solid hemispherical toy is 3.5 cm. Find its total surface area.
View SolutionA hemisphere, the diameter of whose base is equal to the side of a cube, is placed upon the upper face of the cube. If the side of the cube is 14 cm, find the total surface area of the solid combination.
View SolutionThe side of a cube is 21 cm. A hemisphere whose base diameter is equal to the side of the cube is scooped out from one of the faces. Find the total surface area of the solid so obtained
View SolutionA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the surface area of the solid.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of `pi`.
View SolutionRachel, an engineering student, was asked to make a model shaped like a cyclinder. with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model the Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
View SolutionA gulab jamun, containssugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
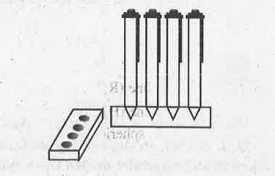
View SolutionA pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.
View SolutionA vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out.Find the number of lead shots dropped in the vessel.
View SolutionA solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 `cm^3` of iron has approximately 8 g mass. (Use `pi` = 3.14)
View SolutionA solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed uprightina right circular cylinder full of water such that it touches the bottom..Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm
View SolutionA spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter, the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be `345 cm^3`. Check whether she is correct, taking the above as the inside measurements, and `pi` = 3.14.
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View SolutionA circus tent is cylindrical upto a height of 3 m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53 m, find the total cost of the canvas used to make the tent when the cost per square metre of the canvas is ? 10.
View SolutionA tent is the form of a cylinder of diameter 15 m and height 2.4 m, surmounted by a cone of equal base and height 4 m. Find the capacity of the tent and the cost of the canvas at Rs. 50 per square metre.
View SolutionThe interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4 m, surmounted by a cone. The vertical height of the cone is 2.1 m. Find the outer surface area and volume of the building.
View SolutionA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the surface area of the solid.
View SolutionA solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 108 cm and the diameter of the hemispherical ends is 36 cm, find the cost of polishing the surface of the solid at the rate of 10 paise per `cm^2`.
View SolutionA well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to a width of 5 m do form an embankment. Find the height of the embankment.
View Solution50 circular plates each of radius 7 cm and 1 thickness `1/2` cm are placed one above another to form a solid right circular cylinder. Find the total surface area and volume of the cylinder so formed.
View SolutionA sphere of diameter 5 cm is dropped into a cylindrical vessel partly filled with water. The diameter of the base of the vessel is 10 cm. If the sphere is completely submerged, by how much will the level of water rise ?
View Solution500 persons took dip in a rectangular tank which is 80 m long and 50 m broad. What is the rise in the level of water in the tank. If the average displacement of water by a person is `0.04 m^3`?
View SolutionA hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to filled into cylindricalshaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl ?
View SolutionWater flows out through a circular pipe, whose internal diameter is 2 cm, at the rate of 0.7 m per second into a cylindrical tank, the radius of whose base is 40 cm. By how much will the level of water rise in half an hour ?
View SolutionThe rain water from a roof `22 m xx 20 m` drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the vessel is just full, find the rainfall in cm
View SolutionA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
View SolutionThe diameter of a copper sphere is 6 cm. The sphere is melted and is drawn into a long wire of uniform circular cross section. If the length of the wire is 36 cm, find its radius.
View SolutionA sphere of radius 8 cm is melted and recast into a right circular cone of height 32 cm. Find the radius of the base of the cone
View SolutionA metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained ?
View SolutionA solid sphere of radius 3 cm is melted and then recast into small spherical balls each of diameter 0.6 cm. Find the number of small balls thus obtained.
View SolutionThree solid glass balls of radii 1 cm, r cm and 8 cm are melted into a solid sphere of radius 9 cm, Determine the value of r.
View SolutionThe internal and external radii of a hollow sphere are 3 cm and 5 cm respectively. The sphere is melted to form a solid cylinder of height `2 frac(2)(3) ` cm . find the diameter and curved surface area of the cylinder.
View SolutionThe base radius and height of a right circular solid cone are 2 cm and 8 cm respectively. It is melted and recast into spheres of diameter 2 cm each. Find the number of spheres so formed.
View SolutionThe internal and external diameters of a hollow hemispherical shell are 6 cm and 10 cm respectively.It is melted and recast into a solid cone of base diameter 14 cm. Find the height of the cone so formed
View SolutionThe sum of the radius of the base and the height of a solid cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 `cm^2`, find the volume of the cylinder.
View SolutionA cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m/s. Calcuate in minutes the time it takes to fill the tank.
View SolutionThe volumes of a sphere and a right circular cylinder are equal and the diameter of the sphere equalsthe dianieter of the base of the cylinder. Determine the height of the cylinder in terms of the diameter of the sphere.
View SolutionLead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm, find the number of lead spheres dropped in the water.
View SolutionA vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, onefourth of the water flows out. Find the number of lead shots dropped in the vessel.
View SolutionA path 2 m wide surrounds a circular pond of diameter 40 m. How many cubic metres of gravel are required to gravel the path to a depth of 20 cm ?
View SolutionA lead pencil consists of cylinder of wood with a solid cylinder of graphite fitted into it. The diameter of the pencil is 7 mm. the diameter of the graphite is 1 mm and the length of the pencil is 10 cm. Calculate the weight of the whole pencil in grams correct to three places of decimals if the specific gravity of the the wood is 0.6 and of the graphite 2.3.
View Solution
Excercise questions and complete solutions for chapter Surface Areas And Volumes of MBD of Class 10