Complete Solutions to EXERCISE of chapter বৃওস্থ স্কোন সম্পর্কিত উপপাদ্য of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | বৃওস্থ স্কোন সম্পর্কিত উপপাদ্য |
| NCERT BANGLISH (BANGLISH MEDIUM) | EXERCISE |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC , BC -এর যে পার্শ্বে `triangleABC` অবস্থিত, সেই পার্শ্বেই `triangleDBC` এমনভাবে অঙ্কন করা হলো যাতে `angleBAC=2angleBDC` হয়। প্রমান করি যে, A -কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে তা D বিন্দু ওই বৃত্তের উপর অবস্থিত হবে ।
05:42View SolutionABC সমদ্বিবাহু ত্রিভুজের AB=AC। সমদ্বিবাহু ত্রিভুজটির পরিকেন্দ্র O এবং BC বাহুর যেদিকে A বিন্দু অবস্থিত তার বিপরীত পার্শ্বে কেন্দ্র O অবস্থিত ।`angleBOC=100^@` হলে `angleABC` ও `angleABO`- এর মান হিসাব করে লিখি ।
05:00View Solutionপাশের চিত্রে `triangleABC` -এর পরিবৃত্তের কেন্দ্র O এবং `angleAOC=110^@`, `angleABC` -এর মান হিসাব করে লিখি ।
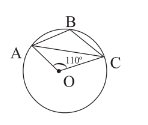 02:41View Solution
02:41View SolutionO কেন্দ্রীয় বৃত্তের ABCD একটি বৃত্তস্থ চতুর্ভুজ। DC বাহুকে P বিন্দু পর্যন্ত বর্ধিত করা হলো । `angleBCP=108^@` হলে, `angleBOD`-এর মান হিসাব করে লিখি ।
01:54View Solutionপাশের চিত্রে O কেন্দ্রীয় বৃত্তের `angleAOD=40^@` এবং `angleACB=35^@`, `angleBCO` ও `angleBOD` -এর মান হিসাব করে লিখি ও উত্তরের সপক্ষে যুক্তি দিই ।
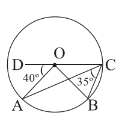 03:44View Solution
03:44View Solutionপাশের চিত্রের O কেন্দ্রীয় বৃত্তের `angleAPB=80^@` হলে, `angleAOB` ও `angleCOD`-এর মানের সমষ্টি নির্ণয় করি ও উত্তরের সপক্ষে যুক্তি দিই।
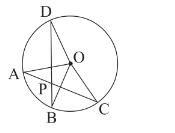 03:46View Solution
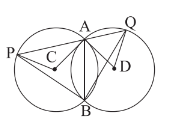
03:46View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, `anglePBQ=angleCAD`
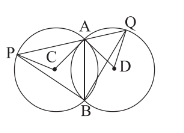 04:19View Solution
04:19View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, `angleBPC=angleBQD`
 07:21View Solution
07:21View SolutionABC ত্রিভুজের পরিকেন্দ্র O , প্রমান করি যে, `angleOBC+angleBAC=90^@`
02:20View Solutionদুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করলে, প্রমান করি যে, `triangleBCD` সমবাহু ত্রিভুজ ।
08:51View Solution`triangleABC` -এর পরিবৃত্তের কেন্দ্র S এবং `ADbotBC` হলে, প্রমাণ করি যে `angleBAD=angleSAC`
03:38View SolutionO কেন্দ্রীয় একটি বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে । প্রমাণ করি যে, `angleAOD+angleBOC=2angleBPC`। যদি `angleAOD` ও `angleBOC` পরস্পর সম্পূরক হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি পরস্পর লম্ব ।
07:50View SolutionO কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা- কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করলে, প্রমাণ করি যে,`angleAOC - angleBOD=2angleBPC`
04:46View SolutionABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হলো যেটি B, C ও D বিন্দু দিয়ে যায় । প্রমাণ করি যে, `angleCBD+angleCDB=frac[1][2]angleBAD`
02:06View Solution`triangleABC` -এর পরিকেন্দ্র O এবং OD, BC বাহুর উপর লম্ব। প্রমাণ করি যে `angleBOD=angleBAC`
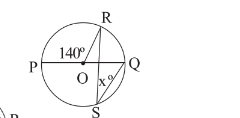
02:52View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে, x- এর মান
 02:51View Solution
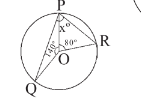
02:51View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র হলে, x -এর মান
 02:39View Solution
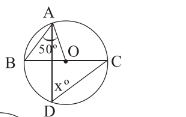
02:39View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং BC ব্যাস হলে, x -এর মান
 03:34View Solution
03:34View SolutionABC ত্রিভুজের O পরিকেন্দ্র । `angleOAB=50^@` হলে, `angleACB` -এর মান
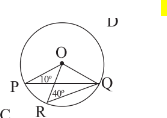
01:47View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র হলে, `anglePOR` -এর মান
 03:31View Solution
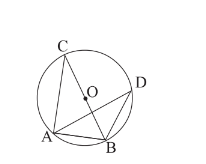
03:31View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র , `angleACB=30^@`,`angleABC=60^@`,`angleDAB=35^@` এবং `angleDBC=x^@` হলে, x- এর মান
 02:00View Solution
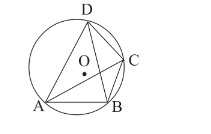
02:00View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র । `angleBAD=65^@`,`angleBDC=45^@` হলে,`angleCBD`-এর মান
 02:12View Solution
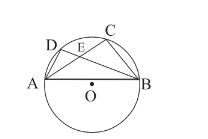
02:12View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র ।`angleAEB=110^@` এবং `angleCBE=30^@` হলে, `angleADB` -এর মান
 02:28View Solution
02:28View SolutionO কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস এবং PR=RQ, `angleRPQ` -এর মান
01:41View SolutionQR বৃত্তের একটি জ্যা এবং POR বৃত্তের একটি ব্যাস । OD, QR বাহুর উপর লম্ব । OD=4 সেমি হলে PQ-এর দৈর্ঘ্য
03:14View SolutionAOB বৃত্তের ব্যাস । AC এবং BD জ্যা দুটি বর্ধিত করলে E বিন্দুতে মিলিত হয় ।`angleCOD=40^@` হলে, `angleCED` -এর মান
02:20View SolutionAOB বৃত্তের ব্যাস । AC=3 সেমি ও BC=4 সেমি হলে, AB -এর দৈর্ঘ্য
01:20View Solutionসত্য বা মিথ্যা লিখি : পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, `angleAOB=2angleACD`
01:33View Solutionসত্য বা মিথ্যা লিখি : ABC ত্রিভুজাকার ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA=OB এবং `angleAOB=2angleACB`. O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের উপর অবস্থিত হবে ।
01:41View Solutionশুন্যস্থান পূরণ করি : একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের ___।
01:49View Solutionশুন্যস্থান পূরণ করি : O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান ।`angleAPB` ও `angleDQC` বৃত্তস্থ কোণ হলে, কোণ দুটির মান ___।
01:24View Solutionশুন্যস্থান পূরণ করি : একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে, যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান ___।
01:17View SolutionABC ত্রিভুজের পরিকেন্দ্র O এবং D বিন্দু BC বাহুর মধ্যবিন্দু। `angleBAC=40^@` হলে, `angleBOD`-এর মান নির্ণয় করো ।
01:48View SolutionO কেন্দ্রীয় বৃত্তের উপর A, B, C তিনটি বিন্দু এমনভাবে অবস্থিত যে AOCB সামান্তরিক। `angleAOC`-এর মান নির্ণয় করি ।
01:17View SolutionABC সমদ্বিবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O এবং `angleABC=120^@`, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি হলে, AB বাহুর দৈর্ঘ্য নির্ণয় করি ।
02:38View SolutionA ও B বৃত্তদ্বয় C এবং D বিন্দুতে ছেদ করে । A কেন্দ্রীয় বৃত্তের উপর অপর বৃত্তের কেন্দ্র B অবস্থিত ।`angleCQD=70^@` হলে, `angleCPD` -এর মান নির্ণয় করি ।
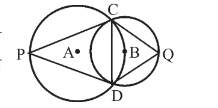 01:43View Solution
01:43View Solutionপাশের ছবিতে `angleDBA=40^@`, `angleBAC=60^@` এবং `angleCAD=20^@`,`angleDCA` ও `angleBCA` -এর মান নির্ণয় করো `angleBAD` ও `angleDCB`-এর মানে সমষ্টি কত হবে হিসাব করে দেখো।
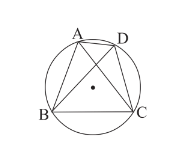 03:15View Solution
03:15View Solutionপাশের চিত্রে AOB বৃত্তের ব্যাস এবং O বৃত্তের কেন্দ্র। OC ব্যাসার্ধ AB -এর উপর লম্ব । যদি উপচাপ CB -এর উপর কোনো বিন্দু P হয়, তবে `angleBAC`ও `angleAPC`-এর মান হিসাব করো।
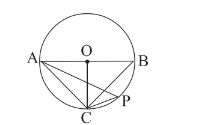 02:50View Solution
02:50View Solution`triangleABC`-এর অন্তর্বৃত্তের কেন্দ্র I, বর্ধিত AI ত্রিভুজের পরিবৃত্তকে P বিন্দুতে ছেদ করে। প্রমাণ করো যে, PB=PC=PI
02:54View Solutionসত্য বা মিথ্যা লেখো : ABC ত্রিভুজের AB=AC, BE ও CF যথাক্রমে `angleABC`ও `angleACB` -এর সমদ্বিখণ্ডক এবং AC ও AB যথাক্রমে E ও F বিন্দুতে ছেদ করে । B, C, E, F বিন্দু চারটি সমবৃত্তস্থ নয় ।
02:04View Solutionশুন্যস্থান পূরণ করো : একই বৃতাংশস্থ বৃত্তস্থ কোণ ___।
01:07View Solutionশুন্যস্থান পূরণ করো : দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে সমান সম্মুখ কোণ উৎপন্ন করলে বিন্দু চারটি __ হবে ।
01:53View Solutionশুন্যস্থান পূরণ করো : একই বৃত্তে দুটি চাপ দ্বারা উৎপন্ন বৃত্তস্থ কোণ দুটি সমান হলে চাপ দুটির দৈর্ঘ্য ___।
02:19View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র, AC ব্যাস এবং জ্যা DE ও ব্যাস AC সমান্তরাল ।`angleCBD=60^@` হলে, `angleCDE`-এর মান নির্ণয় করো ।
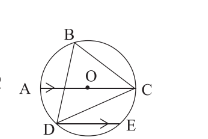 04:05View Solution
04:05View Solutionপাশের চিত্রে `anglePQR` -এর সমদ্বিখণ্ডক QS , `angleSQR=35^@`এবং `anglePRQ=32^@` হলে,`angleQSR` -এর মান নির্ণয় করো ।
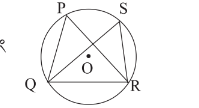 02:50View Solution
02:50View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । AB ও CD পরস্পর লম্ব এবং `angleADC=50^@`,`angleCAD`-এর মান নির্ণয় করো ।
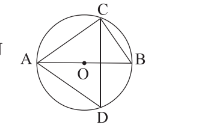 03:34View Solution
03:34View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB=AC ,`angleABC=32^@` হলে, `angleBDC` -এর মান নির্ণয় করো ।
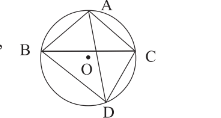 02:50View Solution
02:50View Solutionপাশের চিত্রে BX ও CY যথাক্রমে `angleABC` ও `angleACB` -এর সমদ্বিখণ্ডক। AB=AC এবং BY=4 সেমি হলে, AX -এর দৈর্ঘ্য নির্ণয় করো ।
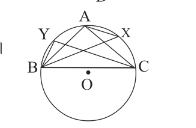 02:58View Solution
02:58View SolutionABC ত্রিভুজের B কোণটি সমকোণ । যদি AC -কে ব্যাস করে একটি বৃত্ত অঙ্কন করো যা AB -কে D বিন্দুতে ছেদ করে, তবে নীচের তথ্যগুলির মধ্যে কোনটি ঠিক লেখো - `ABgtAD`
02:16View SolutionABC ত্রিভুজের B কোণটি সমকোণ । যদি AC -কে ব্যাস করে একটি বৃত্ত অঙ্কন করো যা AB -কে D বিন্দুতে ছেদ করে, তবে নীচের তথ্যগুলির মধ্যে কোনটি ঠিক লেখো - AB=AD
02:22View SolutionABC ত্রিভুজের B কোণটি সমকোণ । যদি AC -কে ব্যাস করে একটি বৃত্ত অঙ্কন করো যা AB -কে D বিন্দুতে ছেদ করে, তবে নীচের তথ্যগুলির মধ্যে কোনটি ঠিক লেখো -(iii) `ABltAD`
02:16View Solutionপ্রমাণ করো যে একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির যে - কোনোটিকে ব্যাস করে অঙ্কিত বৃত্ত অসমান বাহুটিকে সমদ্বিখন্ডিত করে ।
03:11View Solutionসাহানা দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে, প্রমান করো যে A, Q ও B বিন্দুত্রয় সমরেখ ।
03:15View Solutionরজত একটি সরলরেখাংশ PQ অঙ্কন করেছে যার মধ্যবিন্দু R এবং সে PR ও PQ -কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে । আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমান করো যে, PS = ST
06:22View Solutionএকটি বৃত্তের উপর তিনটি বিন্দু P, Q ও R অবস্থিত । PQ ও PR -এর উপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, RQ=ST
05:35View SolutionABC একটি সূক্ষ্মকোণী ত্রিভুজ । ABC ত্রিভুজের পরিবৃত্তের ব্যাস AP, BE ও CF যথাক্রমে AC ও AB বাহুর উপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করে । প্রমাণ করো যে, BPCQ একটি সামান্তরিক ।
08:28View Solutionএকটি ত্রিভুজের শীর্ষকোণের অন্তসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক ত্রিভুজটির পরিবৃত্তকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে । প্রমাণ করো যে, PQ বৃত্তের একটি ব্যাস ।
04:40View SolutionAB এবং CD একটি বৃত্তের ব্যাস । প্রমাণ করো যে, ABCD একটি আয়তকার চিত্র ।
04:08View Solutionপ্রমাণ করি, একটি রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যায় ।
03:29View Solutionসত্য বা মিথ্যা লেখো : অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্যাংশস্থ কোণ স্থূলকোণ ।
01:19View Solutionসত্য বা মিথ্যা লেখো : ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু O এবং OA=OB=OC, AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি C বিন্দু দিয়ে যাবে ।
03:17View Solutionশুন্যস্থান পূরণ করো : অর্ধবৃত্তস্থ কোণ ___।
01:43View Solutionশুন্যস্থান পূরণ করো : অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্যাংশস্ত কোণ ___।
02:42View Solutionশুন্যস্থান পূরণ করো : সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি ___ বিন্দু দিয়ে যাবে ।
02:02View SolutionABC সমদ্বিবাহু ত্রিভুজের AB=AC , AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে, BD=4 সেমি হলে CD -এর দৈর্ঘ্য নির্ণয় করো ।
04:08View Solutionএকটি বৃত্তের দুটি জ্যাABও AC পরস্পর লম্ব।AB=4 সেমি ওAC=3 সেমি হলে বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।
03:35View Solutionএকটি বৃত্তে দুটি জ্যা PQ এবং PR লম্ব। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি হলে, জ্যা QR এর দৈর্ঘ্য নির্ণয় করো।
03:40View SolutionAB বৃত্তের একটি ব্যাস । C বৃত্তের উপর একটি বিন্দু । `angleABC=60^@` হলে `angleCAB` -এর মান নির্ণয় করি ।
02:29View Solutionপাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । জ্যা CD -এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্যের সমান । AC ও BD কে বর্ধিত করায় P বিন্দুতে ছেদ করে । `angleAPB` -এর মান নির্ণয় করি ।
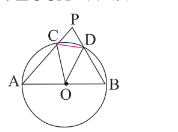 04:53View Solution
04:53View Solution
EXERCISE questions and complete solutions for chapter বৃওস্থ স্কোন সম্পর্কিত উপপাদ্য of NCERT Mathematics (Bengali) of Class 10
