Complete Solutions to EXAMPLE of chapter INTRODUCTION TO TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | INTRODUCTION TO TRIGONOMETRY |
| PSEB | EXAMPLE |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Given tan A =`4/3`, find the other trigonometric ratios of the angle A.
View SolutionIf `angle B` and `angle Q` are acute angles such that sin B = sin Q, then prove that `angleB = angle Q`.
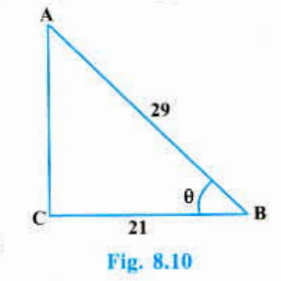
View SolutionConsider `Delta ACB`. right-angled at C, in which AB = 29 units, BC = 21 units and `angle ABC = theta` (see Fig) Determine the values of (i) `cos^2 theta + sin^2 theta`, (ii) `cos^2 theta -sin^2 theta`.
View SolutionIn a right angled triangle ABC, right angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
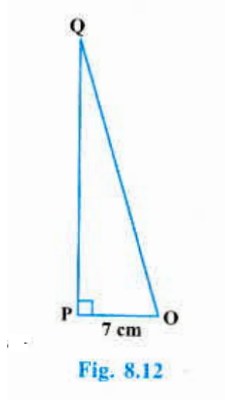
View SolutionIn `Delta OPQ`, right-angled at P, OP= 7 cm and OQ - PQ = 1cm (see Fig. 8.12). Determine the values of sin Q and cos Q.
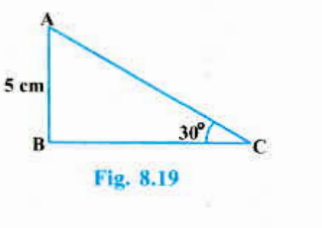
View SolutionIn `Delta ABC`, right-angled at B. AB = 5 cm and `angle ACB =30^@` (see Fig. 8.19). Determine the lengths of the sides BC and AC.
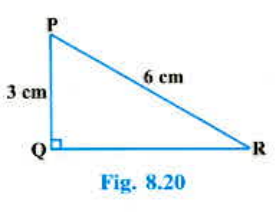
View SolutionIn `Delta PQR`, right-angled at Q (see Fig), PQ = 3 cm and PR = 6 cm. Determine `angle QPR` and `angle PRQ`.
View SolutionIf sin (A-B)=`1/2` , cos(A+B)=`1/2` . Find A and B.
View SolutionEvaluate `(tan 65^@)/(cot 25^@)`
View SolutionIf sin 3A = cos (A- `26^@`) where 3A is an acute angle, find the value of A.
View SolutionExpress cot `85^@` + `cos 75^@` in terms of trigonometric ratios of angles between `0^@` and `45^@`.
View SolutionExpress the ratios cos A, tan A and sec A in terms of sin A.
View SolutionProve that sec A (1 -sin A) (sec A + tan A) =1.
View SolutionProve the following : `(cot A - cos A)/(cot A + cos A)`= `(cosec A -1)/(cosec A + 1)` .
View SolutionProve that `(sin theta-cos theta+1)/(sin theta+cos theta-1)=1/(sec theta-tan theta)`,using the identity `sec^2 theta=1+tan^2 theta`.
View Solution
EXAMPLE questions and complete solutions for chapter INTRODUCTION TO TRIGONOMETRY of PSEB of Class 10