Complete Solutions to EXERCISE of chapter INTRODUCTION TO TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | INTRODUCTION TO TRIGONOMETRY |
| PSEB | EXERCISE |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
In `triangleABC`, right angled at B, AB = 24 cm ,BC = 7 cm. Determine :- sinA, cosA.
View SolutionIn `triangleABC`, right angled at B, AB = 24 cm ,BC = 7 cm. Determine :- sinC, cosC.
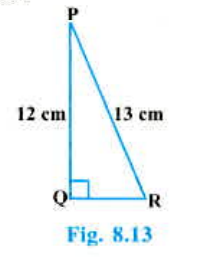
View SolutionIn Fig. 8.13, find `tan P-cot R`.
View SolutionIf sin A = `3/4` calculate cos A and tanA.
View SolutionGiven 15 cot A =8, find sin A and sec A.
View SolutionGiven `sec theta=13/12`, calculate all other trigonometric ratios.
View Solutionif `angleA` and `angleB` are acute angles such that cos A = cos B , show that `angleA=angleB` .
View SolutionIf `cot theta=7/8`, evaluate:- `((1+sin theta)(1-sin theta))/ ((1+cos theta)(1-cos theta))`
View SolutionIf `cottheta=7/8` evaluate :- `cot^2theta` .
View SolutionIf 3cotA=4, check whether 1-tan ^2 A/ 1+tan ^2 A =cos ^2 A−sin ^2 A or not
View SolutionIn triangle ABC, right angled at B, if tan A = `1/sqrt3` . Find the value of :- sin A cos C + cos A sin C.
View SolutionIn triangle ABC, right angled at B, if tan A = `1/sqrt3` . Find the value of :- cos A cos C -sin A sin C.
View SolutionIn `trianglePQR`, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
View SolutionState whether the following are true or false. Justify your answer. :- The value of tan A is always less than 1.
View SolutionState whether the following are true or false. Justify your answer. :- sec A = `12/5` for some value of angle A.
View SolutionState whether the following are true or false. Justify your answer. :- cos A is abbreviation used for cosecant of angle A.
View SolutionState whether the following are true or false. Justify your answer. :- cot A is product of cot and A.
View SolutionState whether the following are true or false. Justify your answer. :-`sin=4/3` for some angle `theta` .
View SolutionEvaluate The following : `sin 60^@ cos 30^@ + sin 30^@ cos 60^@`
View SolutionEvaluate The following : `2 tan^2 45^@ + cos^2 30^@ -sin^2 60^@`
View SolutionEvaluate The following : `(cos 45^@)/(sec 30^@+cosec 30^@)`
View SolutionEvaluate The following : `(sin 30^@+ tan 45^@ - cosec 60^@)/(sec 30^@+cos 60^@ + cot 45^@)`
View SolutionEvaluate The following : `(5 cos^2 60^@+ 4 sec^2 30^@ -tan^2 45^@)/(sin^2 30^@+ cos^2 30^@)`
View SolutionChoose the correct option and justify your choice.:- `(2tan30^@)/(1+tan^2 30^@)`.
View SolutionChoose the correct option and justify your choice.:- `(1-tan^2 45^@)/(1-tan 45^@)`
View SolutionChoose the correct option and justify your choice.:- sin 2A = 2 sin A is true when A
View SolutionChoose the correct option and justify your choice.:- `(2tan30^@)/(1-tan^2 30^@)` .
View SolutionIf tan(A+B)=`sqrt3` and tan(A-B)=`1/sqrt3` , `0^@angleA+Ble90^@` , A>B, find A and B .
View Solutionsin (A + B) = sin A + sin B.
View SolutionStare whether the Following is true or false. Justify your answer:- The value of sin `theta` increases as `theta` increases.
View SolutionStare whether the Following is true or false. Justify your answer:- The value of cos `theta` increases as `theta` increases.
View SolutionStare whether the Following is true or false. Justify your answer:- `sin theta=cos theta` for all values of `theta`.
View SolutionState whetherthe following are true or false. Justify your answer. :- cot A is not defined for A =`0^@` .
View SolutionEvaluate : `(sin 18^@)/(cos 72^@)`
View SolutionEvaluate : `(tan 26^@)/(cot 64^@)`
View SolutionEvaluate : `cos 48^@-sin 42^@`
View SolutionEvaluate : `cosec 31^@ - sec 59^@`
View SolutionShow that : `tan 48^@ tan 23^@ tan 42^@ tan 67^@ = 1`
View SolutionShow that : `cos 38^@ cos 52^@-sin 38^@ sin 52^@ = 0`
View SolutionIf `tan 2A = cot (A -18^@)`, where 2A is an acute angle, find the value of A.
View SolutionIf tan A = cot B. prove that `A +B = 90^@`.
View SolutionIf `sec 4A = cosec (A - 20^@)`, where 4A is an acute angle, find the value of A.
View SolutionIf A, B and C are interior angles of a triangle ABC, then show that `sin((B+C)/2)= cosfrac(A)(2)`.
View SolutionExpress `sin 67^@ + cos 75^@` in terms of trigonometric ratios Of angles between `0^@` and `45^@`
View SolutionExpress the trigonometric ratios sin A, sec A and tan A In terms of cot A.
View SolutionWrite all the other trigonometric ratios of `angle A` in terms of sec A.
View SolutionEvaluate :- `(sin^2 63^@+sin^2 27^@)/(cos^2 17^@+cos^2 73^@)` .
View SolutionEvaluate: `sin 25^@ cos 65^@ + cos 25^@ sin 65^@`
View SolutionChoose the correct option. Justify your choice : `9sec^2A-9tan^2A=` a. 1 b. 9 c. 8 d. 0
View SolutionChoose the correct option. Justify your choice : `(1+tantheta+sectheta)(1+cottheta-cosectheta)`
View SolutionChoose the correct option. Justify your choice : (sec A + tan A) (1-sin A) = ? a. sec A b. sin A c. cosec A d. cos A
View SolutionChoose the correct option. Justify your choice : `(1+tan^2A)/(1+cot^2A)` a. `sec^2A` b. -1 c. `cot^2A` d. `tan^2A`
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosectheta-cottheta)^2=(1-costheta)/(1+costheta)` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosA)/(1+sinA)+(1+sinA)/(cosA)=2secA` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(tantheta)/(1-cottheta)+(cottheta)/(1-tantheta)=1+secthetacosectheta` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(1+secA)/(secA)=(sin^2A)/(1-cosA)` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(cosA-sinA+1)/(cosA+sinA-1)=cosecA+cotA,` using the identity `coses^2A=1+cot^2A)`
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `sqrt((1+sinA)/(1-sinA))=secA+tanA` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(sintheta-2sin^3theta)/(2cos^3theta-costheta) =tantheta` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `(sin A + cosec A)^2+(cosA+secA)^2=7+tan^2A+cot^2A` .
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. `(cosec A -sin A) (sec A - cos A)=1/(tan A + cot A)` [Hint :Simplify LHS and RHS separately]
View SolutionProve the following identities, where the angles involved are acute angles for which the expressions are defined. : `((1+tan^2A)/(1+cot^2A))=((1-tanA)/(1-cotA))^2=tan^2A` .
View Solution
EXERCISE questions and complete solutions for chapter INTRODUCTION TO TRIGONOMETRY of PSEB of Class 10