Complete Solutions to EXAMPLE of chapter SURFACE AREAS AND VOLUMES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SURFACE AREAS AND VOLUMES |
| PSEB | EXAMPLE |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Rasheed got a playing lop (lattu ) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons.The top is shaped like a cone surmounted by a hemisphere (see Fig 13.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take `pi= 22/7`)

View SolutionThe deco alive block shown in Fig. 13.7 is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm. and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take `pi=22/7`)

View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in Fig, 13.8. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm.If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours, (Take `pi` = 3.14)

View SolutionMayank made a bird-bath for his garden 30 cm in the shape of a cylinder with a hemispherical depression at one end (see Fig, 13.9). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of l he bird- bath. (Take `pi =22/7`)

View SolutionShanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (see Fig. 13.12). If the base of the shed is of dimension 7 m x 15 m, and the height of the cuboidal portion is 8m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 `m^3` and there are 20 workers, each of whom occupy about 0.08 `m^3` space on an average. Then, how much air is in the shed? (Take `pi=22/7`)

View SolutionA juice seller was serving his customers using glasses as shown in Fig, 13.13. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity, (Use `pi` = 3.14.)

View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone.The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take `pi` = 3.14)

View SolutionA cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
View SolutionSelvi's house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m x 1.44 m x 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water front the sump which had been full. Compare the capacity of the tank with that of the sump. (Use `pi`= 3.14)
View SolutionA copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
View SolutionA hemispherical tank full of water is emptied by a pipe at the rate of `3 4/7` litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take `pi=22/7`)
View SolutionThe radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see Fig. 13.21). Find its volume, the curved surface area and the total suface area (Take `pi=22/7`).

View SolutionHanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (seeFig. 13.22). If each `cm^3` of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take `pi=22/7`).

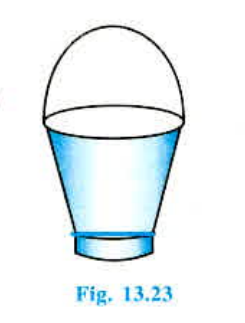
View SolutionAn open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (see Fig. 13.23). The diameters of die two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, Find the volume of water the bucket can hold. (Take `pi=22/7`).
View Solution
EXAMPLE questions and complete solutions for chapter SURFACE AREAS AND VOLUMES of PSEB of Class 10