Complete Solutions to EXERCISE of chapter POLYNOMIALS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYNOMIALS |
| R G PUBLICATION | EXERCISE |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
The graphs of y=P(x) are given below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.

View SolutionThe graphs of y=P(x) are given below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.

View SolutionThe graphs of y=P(x) are given in Fig.2.10 below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.

View SolutionThe graphs of y=P(x) are given in Fig.2.10 below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.
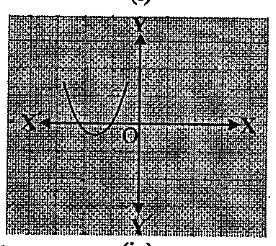
View SolutionThe graphs of y=P(x) are given in Fig.2.10 below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.
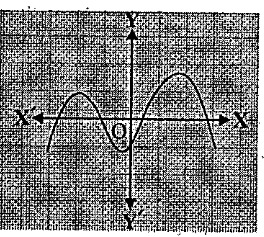
View SolutionThe graphs of y=P(x) are given in Fig.2.10 below,for some polynomials P(x).Find the number of zeroes of P(x),in each case.
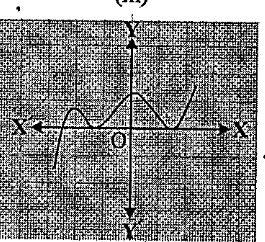
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(i) `x^2-2x-8`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(ii) `4s^2-4s+1`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(iii) `6x^2-3-7x`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(iv) `4u^2+8u`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(v)`t^2-15`
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:(vi)`3x^3-x-4`
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(i)1/4,-1
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(ii)`sqrt2,1/3`
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(iii)`0,sqrt5`
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(iv)1,1
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(v) -1/4,1/4
View SolutionFind a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:(vi) 4,1
View SolutionDivide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:(i) `p(x)=x^3-3x^2+5x-3,g(x)=x^2-2
View SolutionDivide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:(ii)`p(x)=x^4-3x^2+4x+5,g(x)=x^2+1-x`
View SolutionDivide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:(iii)`p(x)=x^4-5x+6,g(x)=2-x^2`
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:(i) `t^2-3,2t^4+3t^3-2t^2-9t-12`
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:(ii)`x^2+3x+1,3x^4+5x^3-7x^2+2x+2`
View SolutionCheck whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:(iii)`x^3-3x+1,x^5-4x^3+x^2+3x+1`
View SolutionObtain all other zeroes of `3x^4+6x^3-2x^2-10x-5`
View SolutionOn dividing `x^3-3x^2+x+2` by a polynomial g(x),the quotient and remainder were x-2 and -2x+4,respectively,Find g(x)
View SolutionGive examples of polynomials p(x),g(x),q(x) and r(x),which satisfy the division algorithm and (i) degp(x)=degq(x)
View SolutionGive examples of polynomials p(x),g(x),q(x) and r(x),which satisfy the division algorithm and (ii)deg q(x)=deg r(x)
View SolutionGive examples of polynomials p(x),g(x),q(x) and r(x),which satisfy the division algorithm and (iii)deg r(x)=0
View SolutionVerify that the numbers given along side of the cubic polynomial below are their zeroes.Also verify the relationship between the zeroes and the coefficients in each case:(i)`2x^3+x^2-5x+2,1/2,1,-2`
View SolutionVerify that the numbers given along side of the cubic polynomial below are their zeroes.Also verify the relationship between the zeroes and the coefficients in each case:(ii)`x^3-4x^2+5x-2`, 2,1,1
View SolutionFind a cubic polynomial with the sum,sum of the product of its zeroes taken two at a time,and the product of its zeroes as 2,-7,-14 respectively.
View SolutionIf the zeroes of the polynomial`x^3-3x^2+x+1` are a-b,a,a+b,find a and b.
View SolutionIf two zeroes of the polynomial `x^4-6x^3-26x^2+138x-35` are `2+-sqrt3`.find other zeroes.
View SolutionIf the polynomial `x^4-6x^3+16x^2-25x+10` is divided by another polynomial `x^2-2x+k`,the ramainder comes out to be x+a,find k and a.
View SolutionIf `alpha,beta` are the zeroes of the polynomial `f(x)=x^2+x+1` then `1/alpha+1/beta`is____
View SolutionThe polynomial is
View SolutionThe zeros of the polynomial `x^2-sqrt2x-12` are
a)`3sqrt2,2sqrt2` b)`sqrt2,-sqrt2` c)`3sqrt2,-2sqrt2` d)`-3sqrt2,2sqrt2`
View SolutionThe zeros of the quadratic polynomial `x^2+99x+127` are
a)equal b)positive c)Negative d)One positive and one negative
View SolutionThe zeros of the quadratic polynomial `x^2+88x+125` are
View SolutionIf `p(x)=ax^2+bx+c` has no real zeroes and a+b+c<0,then
View SolutionIf the zeroes of the quadratic polynomial `ax^2+bx+c`,where `a!=0`and `c!=0` are equal then
View SolutionIf one of the zeroes of the quadratic polynomial `x^2+bx+c`is negative of the other,then
a) b=0 and c is negative b) b=0 and c is positive c)`b!=0` and c is positive d) `b!=0` and c is negative
View SolutionIf one zero of the quadratic polynomial `kx^2+3x+k`is 2,then the value of k is
View SolutionIf -4 is a zero of the polynomial `x^2-x-x-(2+2k) then the value of k is
View SolutionIf one zero of the polynomial `(k-1)x^2+kx+1` is -4,then the value of k is
View SolutionIf one zero of `3x^2+8x+k`be the reciprocal of the other then the value of k is
a)3 b)-3 c)`1/3` d)`(-1)/3`
View SolutionIf one zero of the polynomial `P(x)=(k^2+4)x^2+13x+4k`,is reciprocal of the other then the value of k is
a)1 b)2 c)-2 d)-1
View SolutionIf the polynomial `f(x)=ax^3+bx-c` is divisible by `g(x)=x^2+bx+c`,then the value of ab is
View SolutionIf `alpha,beta` are the zeroes of `f(x)=2x^2+6x-6`,then
a)`alpha+beta+alpha beta=0` b)`alpha+beta=alpha beta` c)`alpha+betagtalpha beta` d)`alpha+betaltalpha beta`
View SolutionIf `alpha,beta` are the zeroes of `2x^2+5x-9`,then the value of `alpha*beta` is
View SolutionIf `alpha,beta` are the zeroes of polynomial `f(x)=x^2-p(x+1)-c`,then `(alpha+1)(beta+1)`=
View SolutionIf `alpha,beta` be the zeroes of polynomial `x^2-8x+k`such that `alpha^2+beta^2=40` then the value of k will be
a)6 b)9 c)12 d)-12
View SolutionIf the product of two zeroes of the polynomial `P(x)=2x^3+6x^2-4x+9` is 3,then its third zero is
a)`3/2` b)`-3/2` c)`9/2` d)`-9/2`
View SolutionTwo zeros of polynomial `ax^3+bx^2+cx+d`are zero then its third zero is
a/b
b/a
-b/a
d/c
View SolutionIf zeros of the polynomial `x^3-3px^2+qx-r` are in A.P.then
View SolutionIf the zeroes of the polynomial `x^3-3x^2+x+1` are a-d,a and a+d then a+d is
a)a natural number b)a rational number c)an irrational number d)an integer
View SolutionIf `alpha,beta`, are the zeroes of the polynomial `ax^2+bx+c`,then `alpha^2+beta^2`=
View SolutionIf `alpha,beta`, be the zeroes of the polynomial `2x^2+5x+k`such that `alpha^2+beta^2+alphabeta=21/4` then k=
View SolutionIf two zeroes of `x^3+x^2-5x-5` are `sqrt5` and `-sqrt5` then its third zero is
a)1 b)2 c)-1 d)-2
View SolutionIf `alpha,beta,gamma` be the zeroes of the polynomial `x^3-6x^2-x+30`, then `alphabeta+betagamma+gammaalpha`=?
View SolutionIf `alpha,beta,gamma`,are the zeroes of the polynomial `2x^3+x^2-13x+6` then `alphabetagamma`=?
a)3 b)-3 c)`(-1)/2` d)`(-13)/2`
View SolutionIf x+2 is a factor of `x^2+ax+2b` and a+b=4 then
a=-1,b=5
a=5,b=-1
a=1,b=3
a=3,b=1
View SolutionIf `alpha,beta,gamma`,are the zeroes of the polynomial `x^3-px^2+qx-r`,then`1/(alphabeta)+1/(betagamma)+1/(gammaalpha)`=?
p/r
-p/r
r/p
-r/p
View SolutionA Quadratic polynomial has three zeroes.True or False
View SolutionPolynomial `ax^2+c` has two zeroes which are equal in magnitude but opposite in sign. True or False
View SolutionEach polynomial has at least one zero. True or False
View SolutionState true or false:
We cannot find zeroes of polynomial `x^4+16`
View SolutionGraph of polynomial `x^2-5x+4`will intersect x axis exactly at two distinct points. True or False
View Solution
EXERCISE questions and complete solutions for chapter POLYNOMIALS of R G PUBLICATION of Class 10