Complete Solutions to पुनरावृत्ति प्रश्नावली of chapter वृत्तों से सम्बन्धित क्षेत्रफल of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | वृत्तों से सम्बन्धित क्षेत्रफल |
| RD SHARMA HINDI | पुनरावृत्ति प्रश्नावली |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
एक समतल में तीन वृत्त इस प्रकार स्थित हैं कि प्रत्येक वृत्त अन्य दो को स्पर्श करता है | प्रत्येक वृत्त की त्रिज्या 10 सेमी. है | वृत्तों के बीच में घिरे हुए भाग का क्षेत्रफल ज्ञात कीजिये |
View Solutionएक ट्रैक्टर के अगले तथा पिछले पहियों के व्यास क्रमश: 80 सेमी. तथा 2 मी. हैं | ज्ञात कीजिये कि पिछला पहिया उस दूरी को तय करने में कितने चक्कर लगायेगा जिसे तय करने में अगला पहिया 1400 चक्कर लगाता है |
View Solutionउस वृत्त का क्षेत्रफल ज्ञात कीजिये जिसमें `64" सेमी."^(2)` क्षेत्रफल वाला वर्ग अंतर्निहित है | `(pi=3.14)`
View Solutionबस के एक पहिये का व्यास 90 सेमी. है यदि वह प्रति मिनट 315 चक्कर लगाता है, तो उसकी चाल किमी प्रति घण्टा में ज्ञात कीजिये ? (दिया है : `pi=22//7`).
View Solutionचित्र में, OE = 20 सेमी. है | त्रिज्यखण्ड OSFT में, वर्ग OEFG अंतर्निहित है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिये |
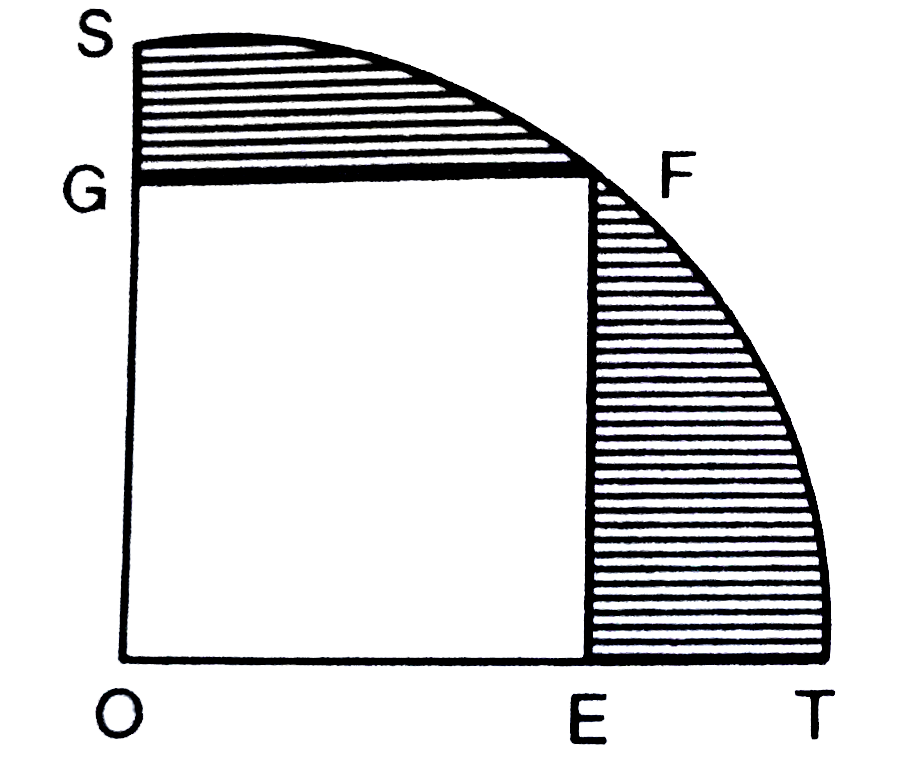
View Solutionचित्र में, 28 सेमी. त्रिज्या वाले वृत्त का केन्द्र O है | लघु वृत्तखण्ड ASB का क्षेत्रफल ज्ञात कीजिये |

View Solutionचित्र में, PQRS एक 4 सेमी. भुजा का वर्ग है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
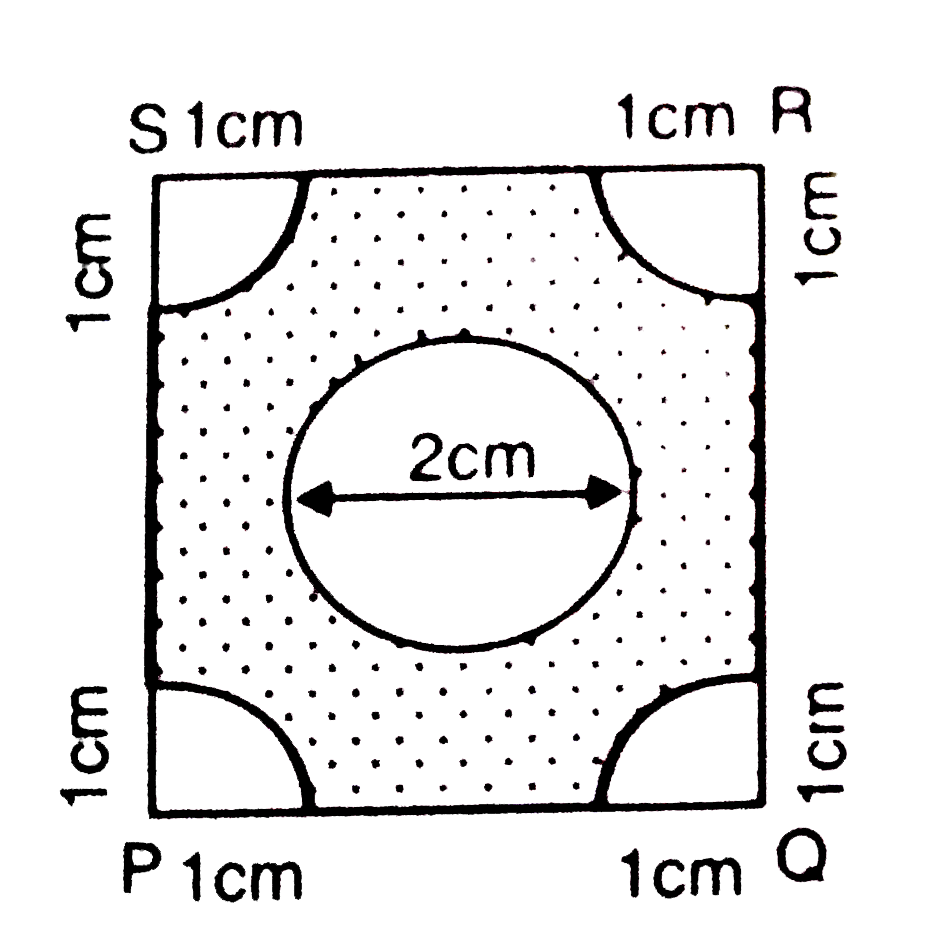
View Solutionचित्र में प्रदर्शित एक बाल्टी 77 सेमी. व्यास वाले पुलि पर बंधी रस्सी की सहायता से एक कुएँ से उठायी जाती है | यदि बाल्टी 1.1 मीटर प्रति सेकेण्ड कि गति से 1 मिनट 28 सेकेण्ड में ऊपर तक आ जाती है, तो बाल्टी को ऊपर तक उठाने में पुलि कुल कितने चक्कर लगायेगी |

View Solutionएक 12 सेमी. भुजा वाले समबाहु त्रिभुज ABC के अन्दर एक वृत्त बनाया गया है, जो इसकी भुजाओं को स्पर्श करता है | वृत्त की त्रिज्या एवं छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, 6 सेमी. भुजा वाला एक समबाहु त्रिभुज ABC एक वृत्त के अन्दर बनाया गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | `(pi=3.14)`
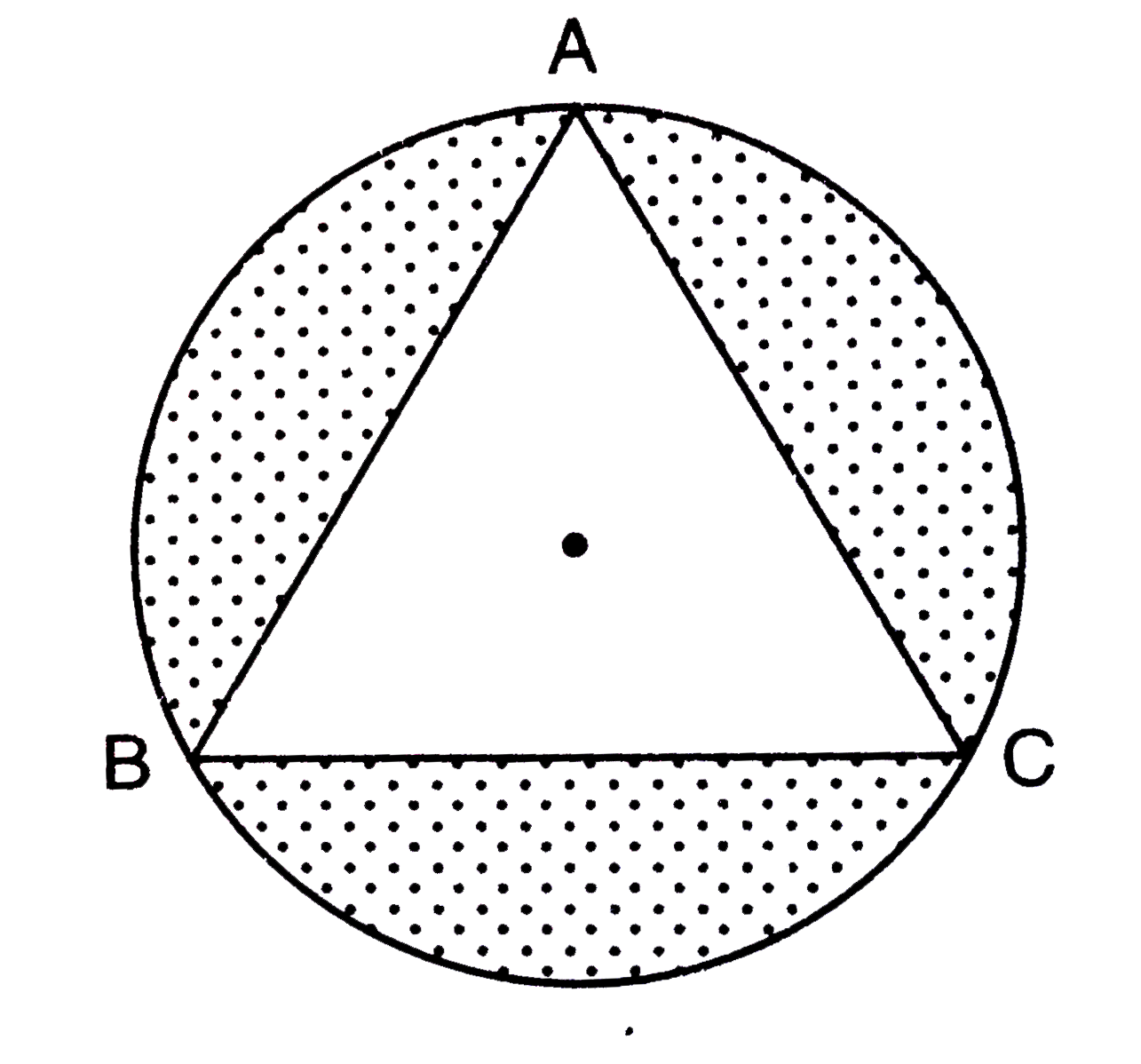
View Solutionएक वृत्ताकार मैदान का परिमाप 650 मीटर है | एक वर्गाकार प्लाट तथा इसके शीर्षों को दिये हुए वृत्ताकार मैदान की परिधि पर चिन्हित किया गया है | वर्गाकार प्लाट का क्षेत्रफल ज्ञात कीजिए |
View Solutionचित्र में, एक वर्ग ABCD को पाँच बराबर भागों में बाँटा गया है, सभी भागों का क्षेत्रफल बराबर है | मध्य भाग में एक वृत्त तथा भुजाएँ AE, GC, BF तथा HD वर्ग के विकर्ण AC तथा BD पर स्थित हैं | यदि AB = 22 सेमी है | तो ज्ञात कीजिए :
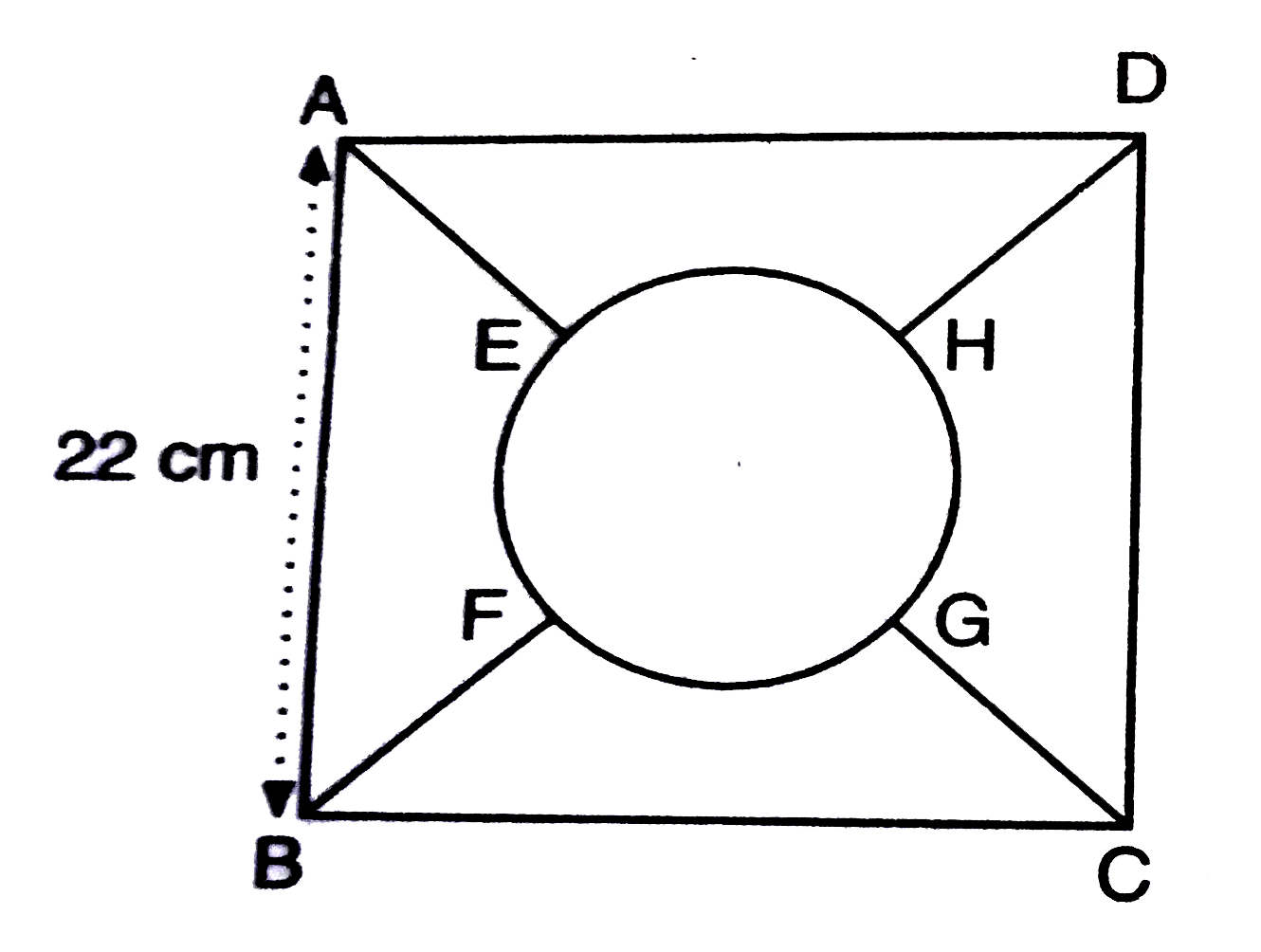
मध्य भाग की परिधि एवं
View Solutionचित्र में, एक वर्ग ABCD को पाँच बराबर भागों में बाँटा गया है, सभी भागों का क्षेत्रफल बराबर है | मध्य भाग में एक वृत्त तथा भुजाएँ AE, GC, BF तथा HD वर्ग के विकर्ण AC तथा BD पर स्थित हैं | यदि AB = 22 सेमी है | तो ज्ञात कीजिए :
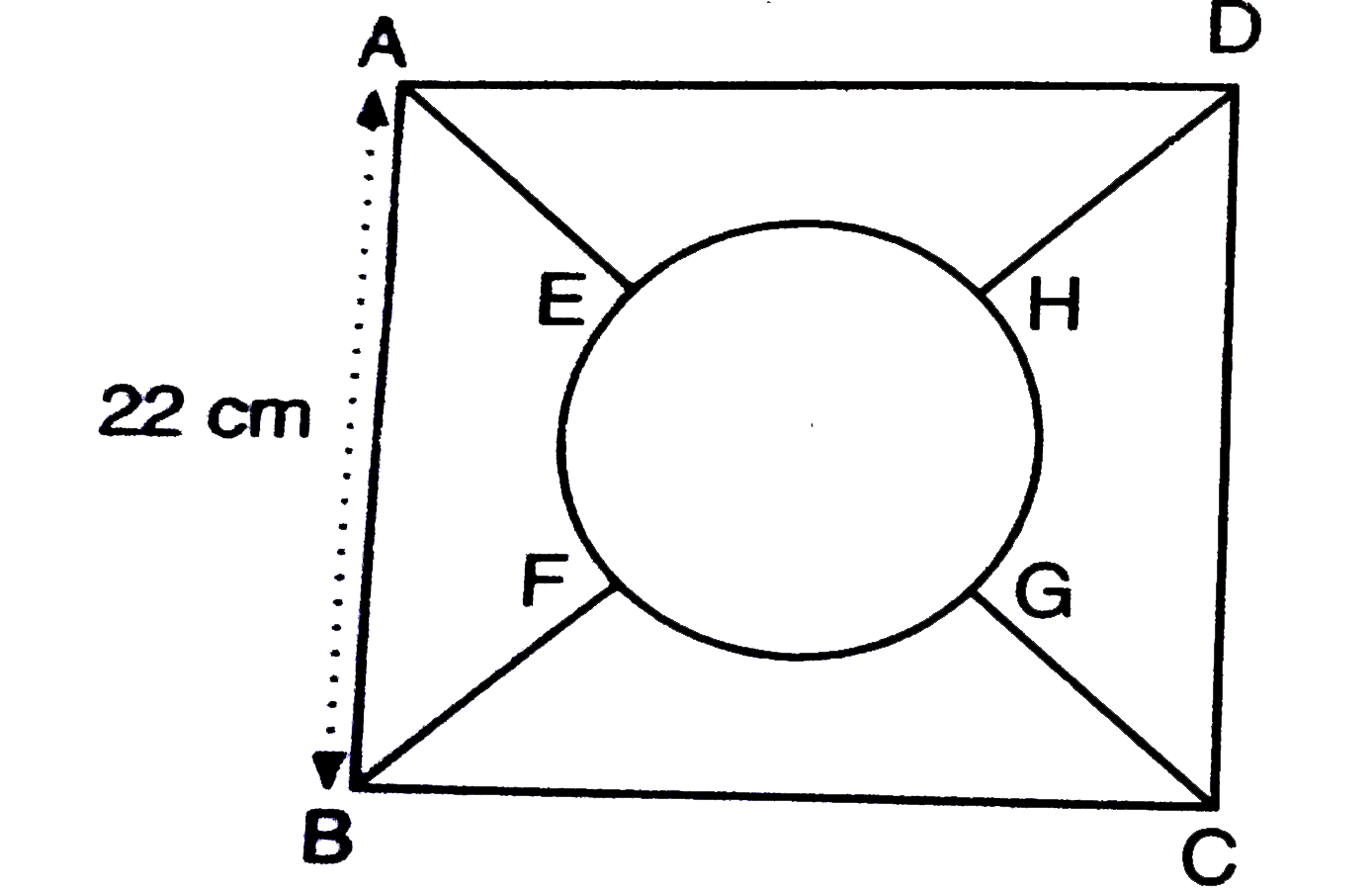
भाग ABEF का परिमाप |
View Solutionचित्र में, ABCD एक आयत है, जिसमें AB = 20 सेमी. तथा BC = 14 सेमी है | इसमें `180^(@)` कोण के दो त्रिज्यखण्ड काटे गये हैं | ज्ञात कीजिए :
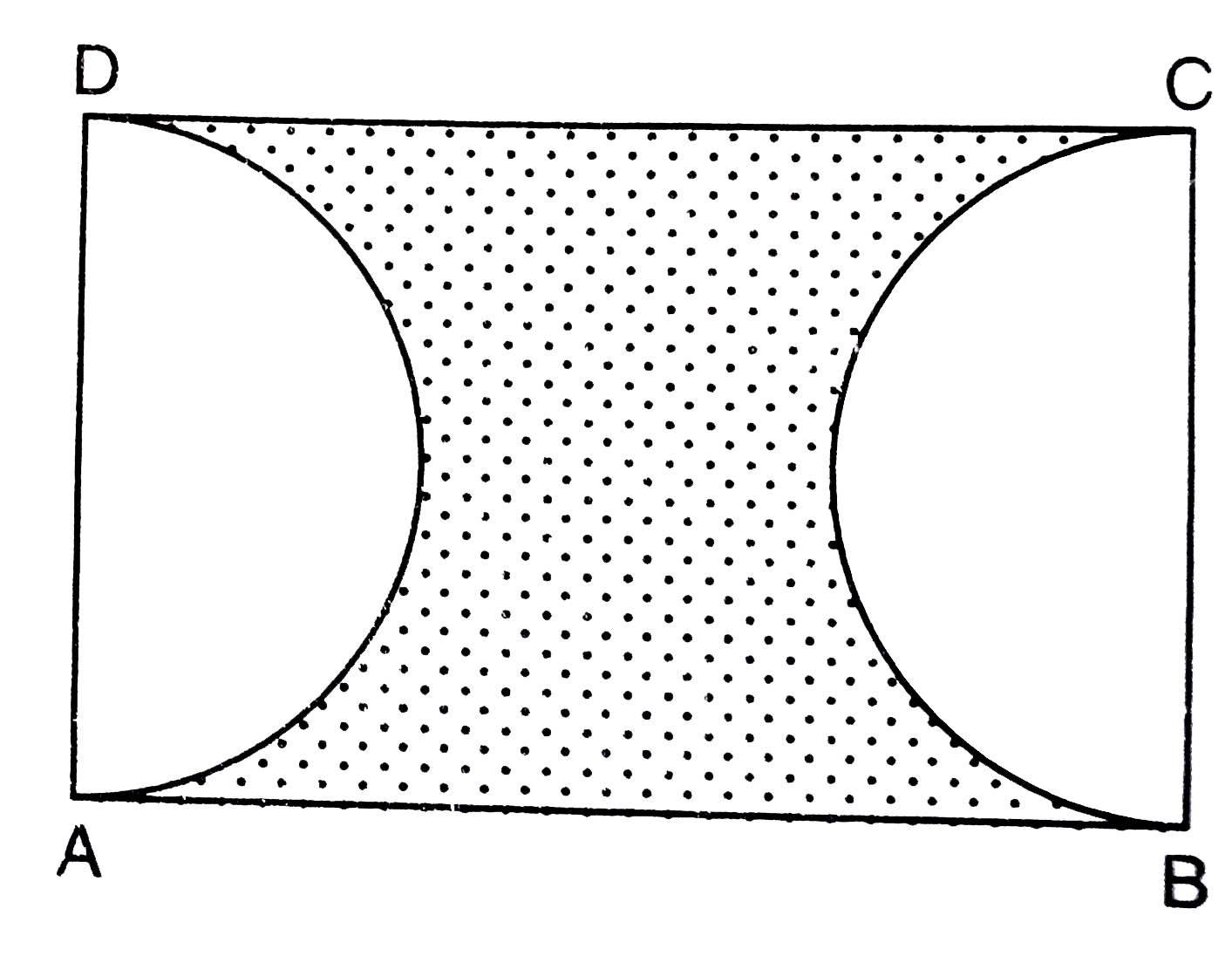
छायांकित भाग का क्षेत्रफल
View Solutionचित्र में, ABCD एक आयत है, जिसमें AB = 20 सेमी. तथा BC = 14 सेमी है | इसमें `180^(@)` कोण के दो त्रिज्यखण्ड काटे गये हैं | ज्ञात कीजिए :
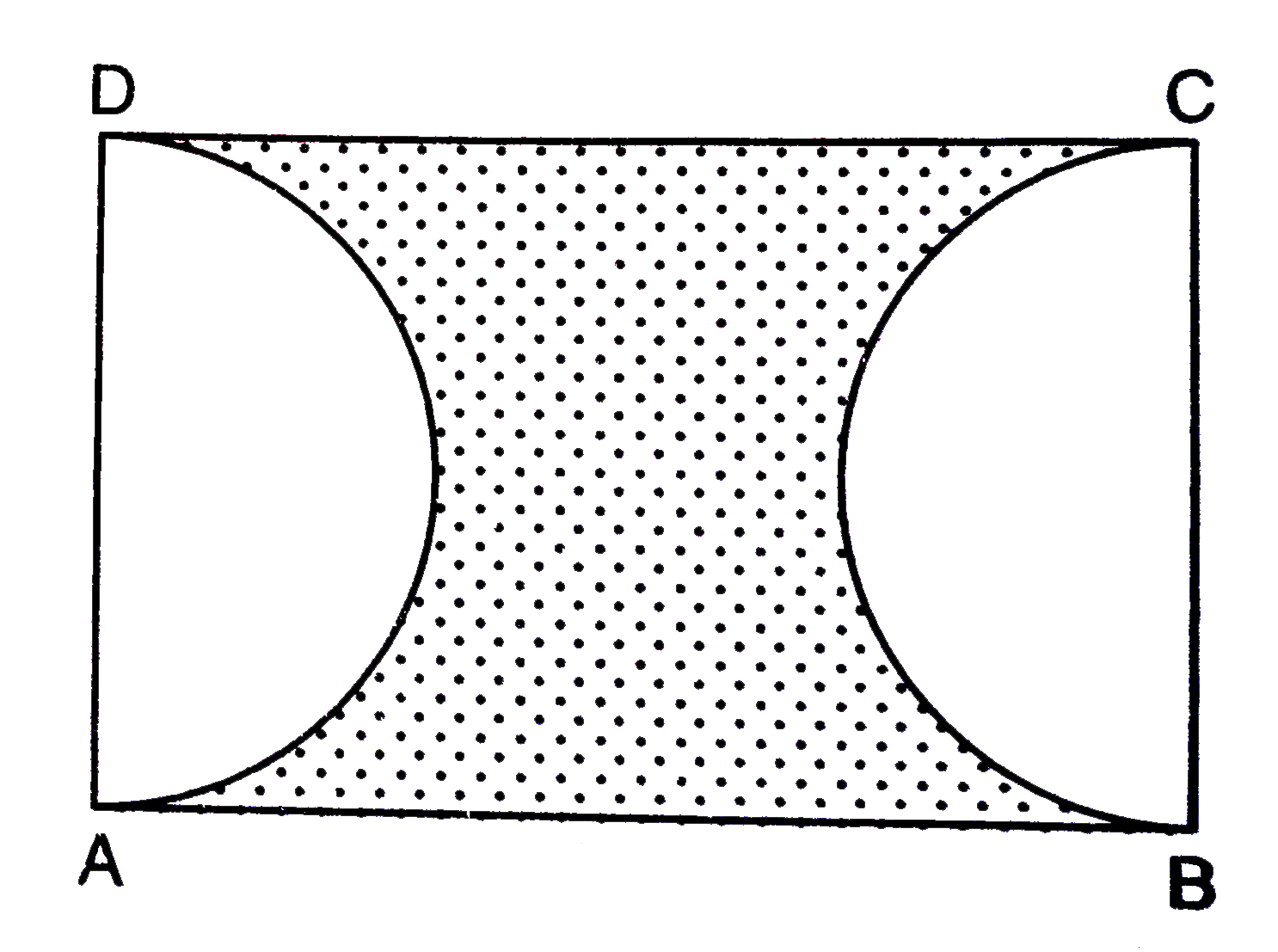
छायांकित भाग का सीमा की लम्बाई |
View Solutionचित्र में, 1 सेमी. व्यास के चार सिक्कों को इस प्रकार मेज पर रखा गया है की उनकी परिधि एक दूसरे से स्पर्श करती हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | `(pi=3.1416)`
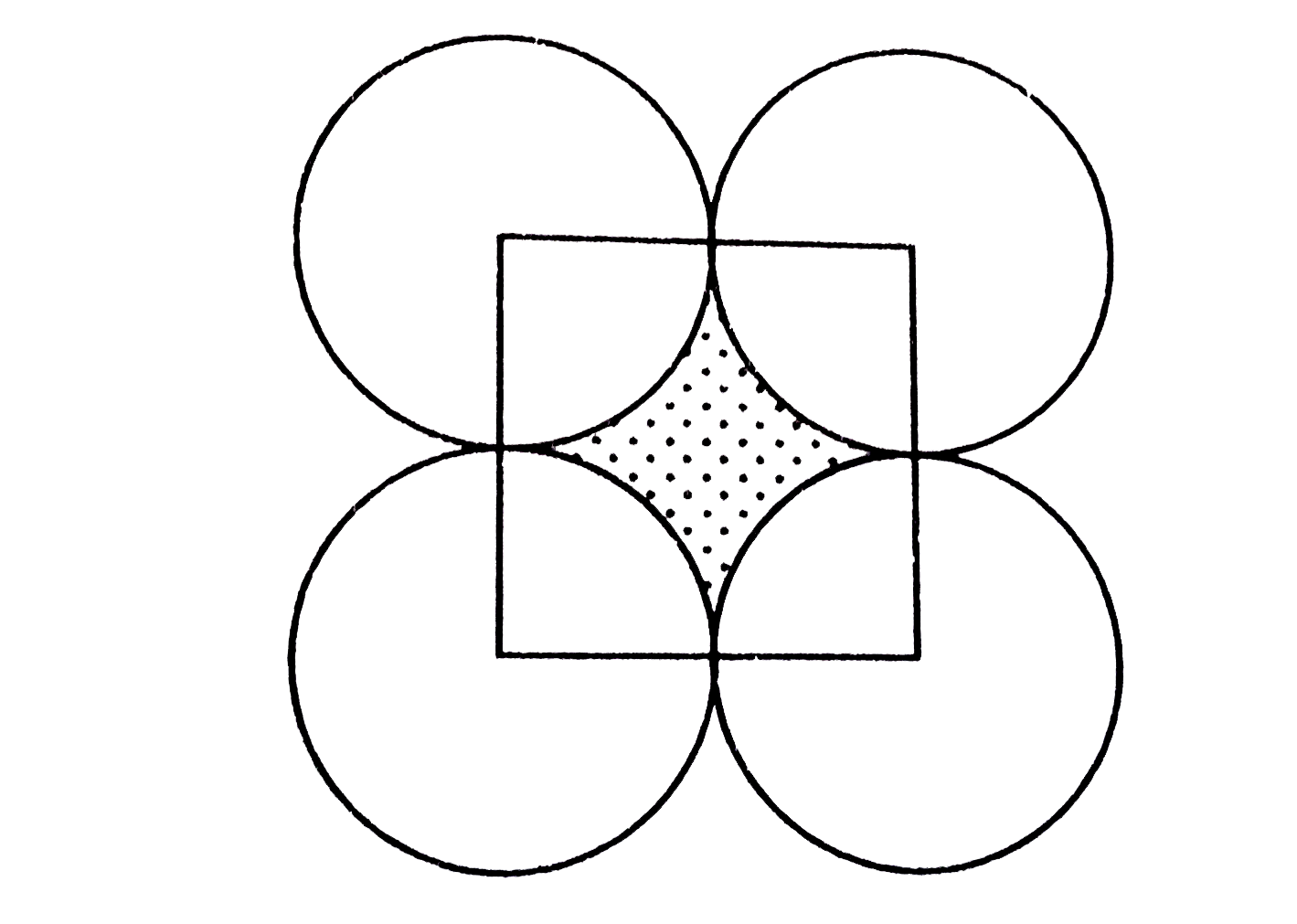
View Solution3 सेमी. त्रिज्या वाले वृत्ताकार कार्डबोर्ड से `90^(@)` के दो त्रिज्यखण्ड काट लिये गये हों, तो शेष भाग का परिमाप नजदीकी सौवें दशमलव अंक तक सेमी. में ज्ञात कीजिए | `(pi=22//7)`
View Solutionएक त्रिज्यखण्ड का क्षेत्रफल एक वृत्त के क्षेत्रफल एक वृत्त के क्षेत्रफल का `1//12` वाँ भाग हो, तो त्रिज्यखण्ड का कोण ज्ञात कीजिए |
View Solutionचित्र में, 5 सेमी त्रिज्या वाले वृत्त का केन्द्र O है | त्रिज्याएँ OA और OB एक दूसरे से समकोण पर खींची गयी है | जीवा AB से बने वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए | `(pi=3.14)`

View Solutionचित्र में, ABCDEF एक षटभुज है जिसका केन्द्र O है | यदि त्रिभुज OAB का क्षेत्रफल 9 वर्ग सेमी. हो, तो
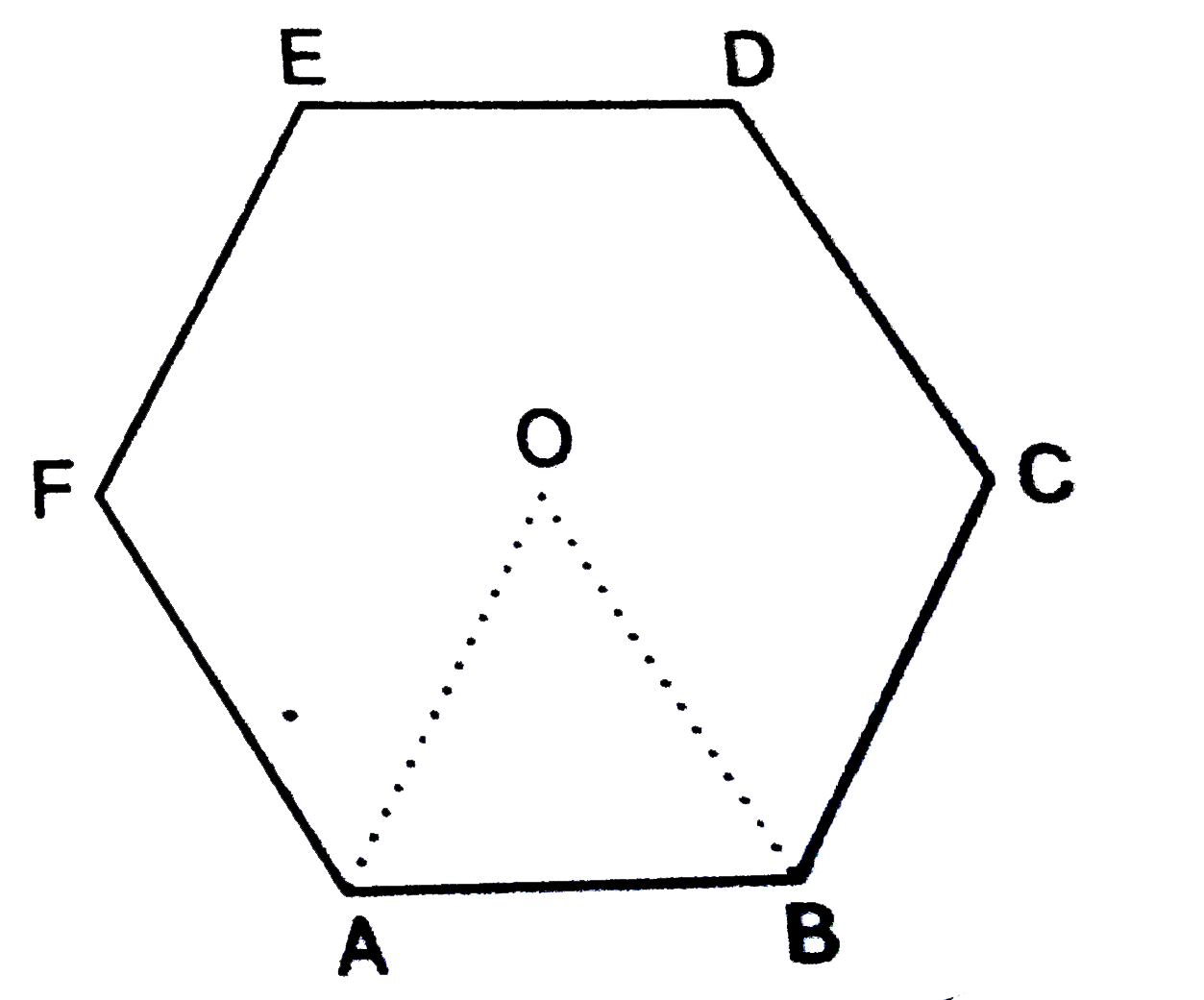
षटभुज तथा
View Solutionचित्र में, ABCDEF एक षटभुज है जिसका केन्द्र O है | यदि त्रिभुज OAB का क्षेत्रफल 9 वर्ग सेमी. हो, तो

एक वृत्त जिसके अन्दर षटभुज बना हो, का क्षेत्रफल ज्ञात कीजिए |
View Solutionएक पतले धातु का टुकड़ा एक समलम्ब चतुर्भुज ABCD के आकार का है, जिसमें `"AB"||"CD"` तथा `angleBCD=90^(@)` है | इसमें से एक चौथाई वृत्त BEFC को काट लिया गया है | यदि AB = BC = 3.5 सेमी. तथा DE = 2 सेमी. हो, तो शेष बचे धातु के टुकड़े का क्षेत्रफल ज्ञात कीजिए |
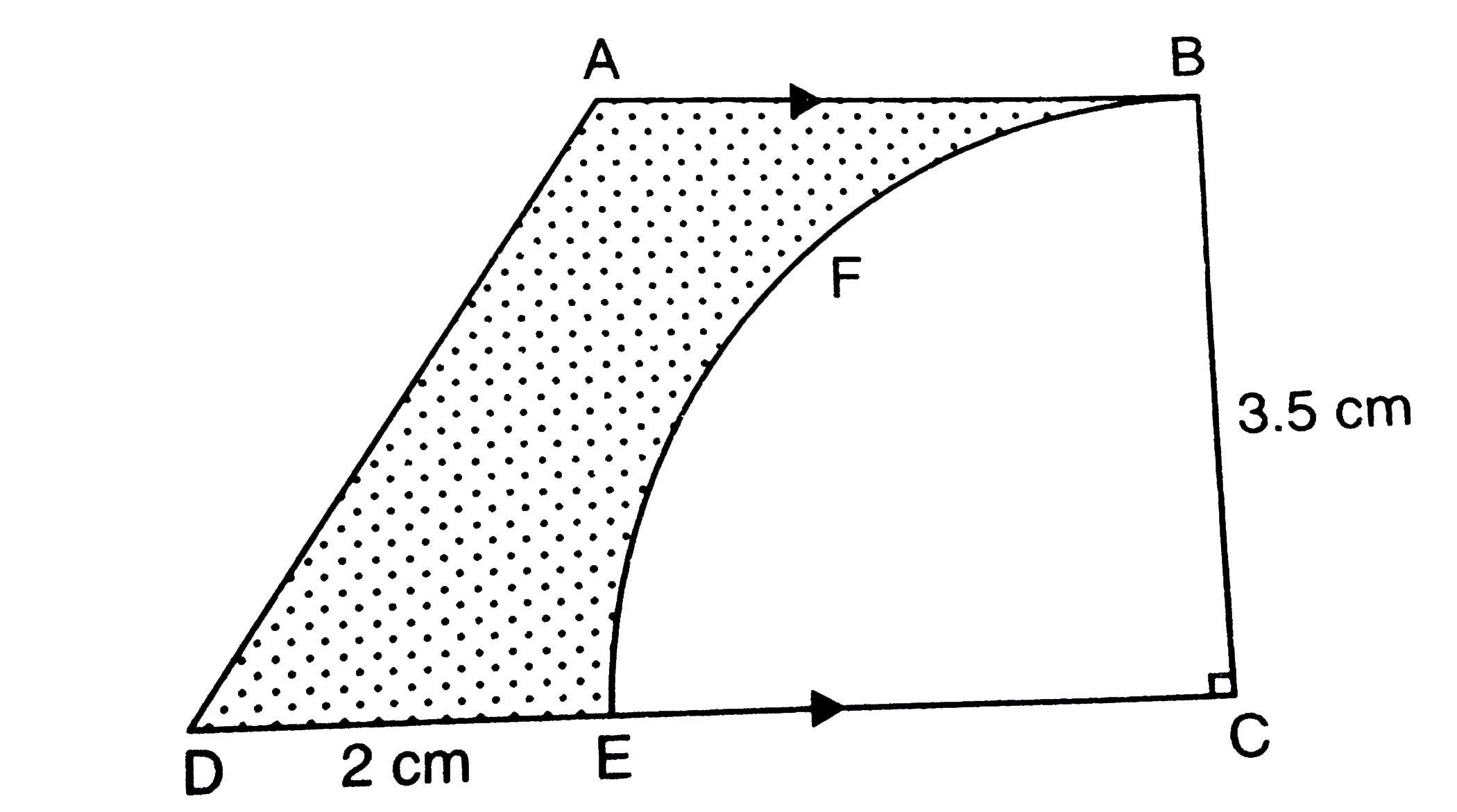
View Solutionत्रिज्या 3.5 सेमी. तथा 7 सेमी वाले दो संकेन्द्रीय वृत्तों का क्षेत्रफल ज्ञात कीजिए | 7 सेमी त्रिज्या वाले वृत्त के बाहर एक तीसरा संकेन्द्रीय वृत्त इस प्रकार खींचा गया है कि इसका क्षेत्रफल शेष दोनों वृत्तों के क्षेत्रफलों के बराबर है | तीसरे वृत्त की त्रिज्या दशमलव के एक स्थान तक ज्ञात कीजिए |
View Solutionएक वृत्ताकार घास के मैदान के चारों ओर 4 मीटर चौड़ा रास्ता है जिसकी परिधि `163(3)/(7)` मीटर हो तो ज्ञात कीजिए :
रास्ते का क्षेत्रफल |
View Solutionएक वृत्ताकार घास के मैदान के चारों ओर 4 मीटर चौड़ा रास्ता है जिसकी परिधि `163(3)/(7)` मीटर हो तो ज्ञात कीजिए :
1.50 रूपये प्रति वर्ग मीटर की दर से रास्ते पर पत्थर बिछाने का खर्च |
View Solutionएक वृत्ताकार घास के मैदान के चारों ओर 4 मीटर चौड़ा रास्ता है जिसकी परिधि `163(3)/(7)` मीटर हो तो ज्ञात कीजिए :
45 पैसे प्रति वर्ग मीटर की दर से मैदान को एकसार करने का खर्च |
View Solutionचित्र में रेलवे सुरंग का अनुप्रस्थ काट दिखाया गया है | वृत्ताकार भाग की त्रिज्या OA 3.5 मीटर है | यदि `angleAOB=90^(@)` हो, तो गणना कीजिए :
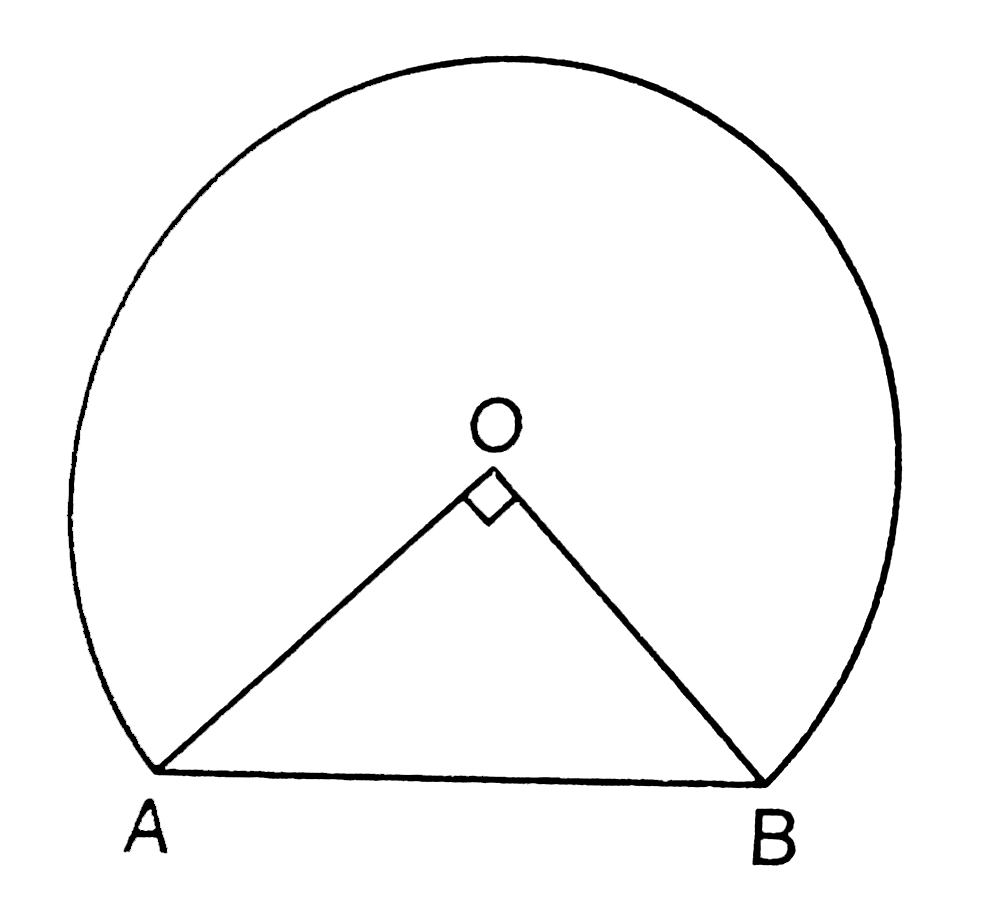
सुरंग की ऊँचाई
View Solutionचित्र में रेलवे सुरंग का अनुप्रस्थ काट दिखाया गया है | वृत्ताकार भाग की त्रिज्या OA 3.5 मीटर है | यदि `angleAOB=90^(@)` हो, तो गणना कीजिए :

अनुप्रस्थ काट का परिमाप, तथा
View Solutionचित्र में रेलवे सुरंग का अनुप्रस्थ काट दिखाया गया है | वृत्ताकार भाग की त्रिज्या OA 3.5 मीटर है | यदि `angleAOB=90^(@)` हो, तो गणना कीजिए :

अनुप्रस्थ काट का क्षेत्रफल |
View Solutionचित्र में ABC समकोण त्रिभुज है जिसमें `angleB=90^(@),AB=28` सेमी. तथा BC = 21 सेमी है | AC को व्यास मानकर एक अर्धवृत्त तथा BC को त्रिज्या मानकर एक चौथाई वृत्त खींचा गया है | दशमलव के दो स्थान तक छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
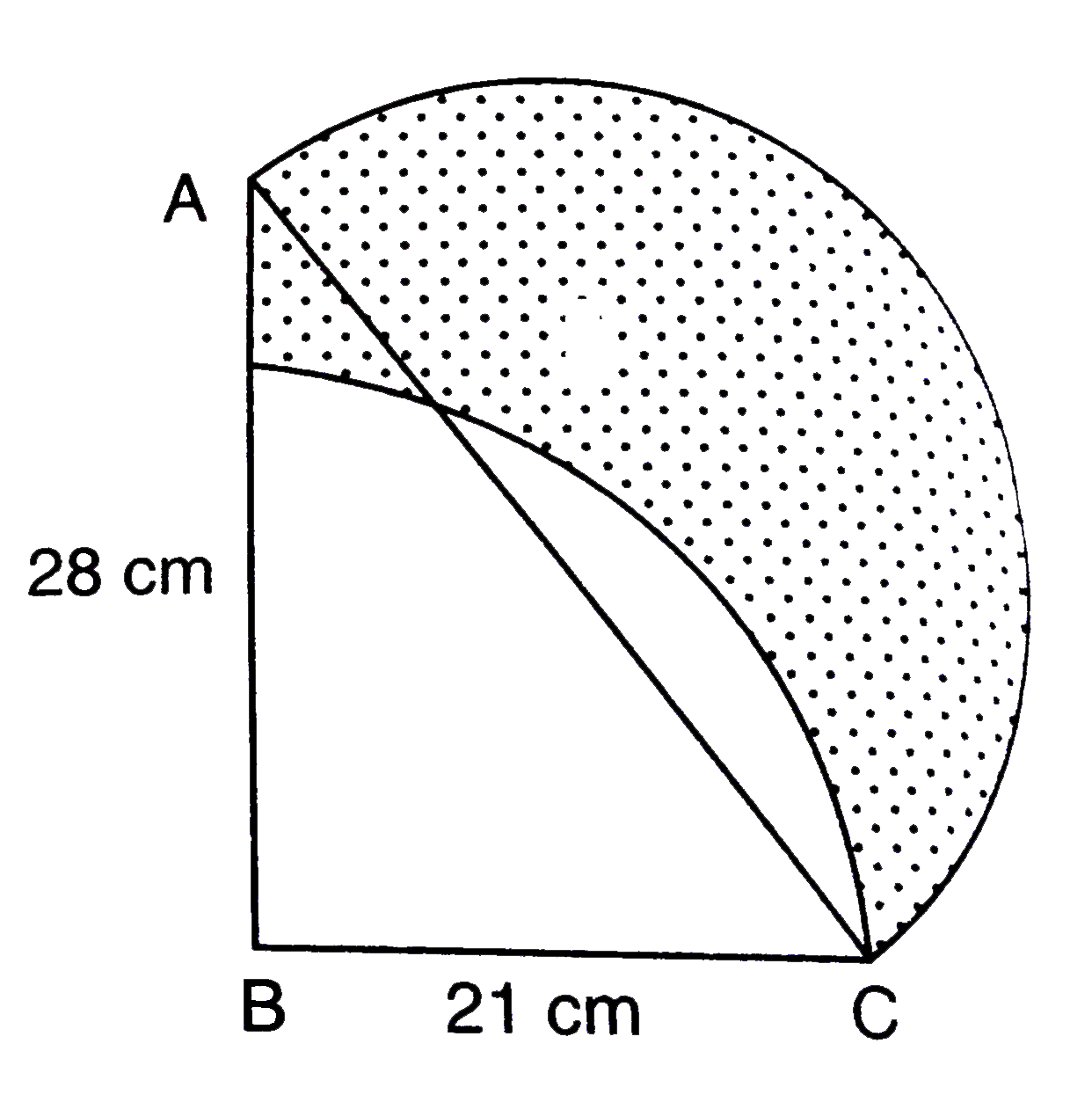
View Solutionचित्र में, तीन अर्धवृत्त A, B तथा C हैं, जिनमें प्रत्येक के व्यास 3 सेमी हैं | एक दूसरा अर्धवृत्त E है जिसके अन्दर 4.5 सेमी व्यास वाला एक वृत्त D है | गणना कीजिए :

छायांकित भाग का क्षेत्रफल |
View Solutionचित्र में, तीन अर्धवृत्त A, B तथा C हैं, जिनमें प्रत्येक के व्यास 3 सेमी हैं | एक दूसरा अर्धवृत्त E है जिसके अन्दर 4.5 सेमी व्यास वाला एक वृत्त D है | गणना कीजिए :
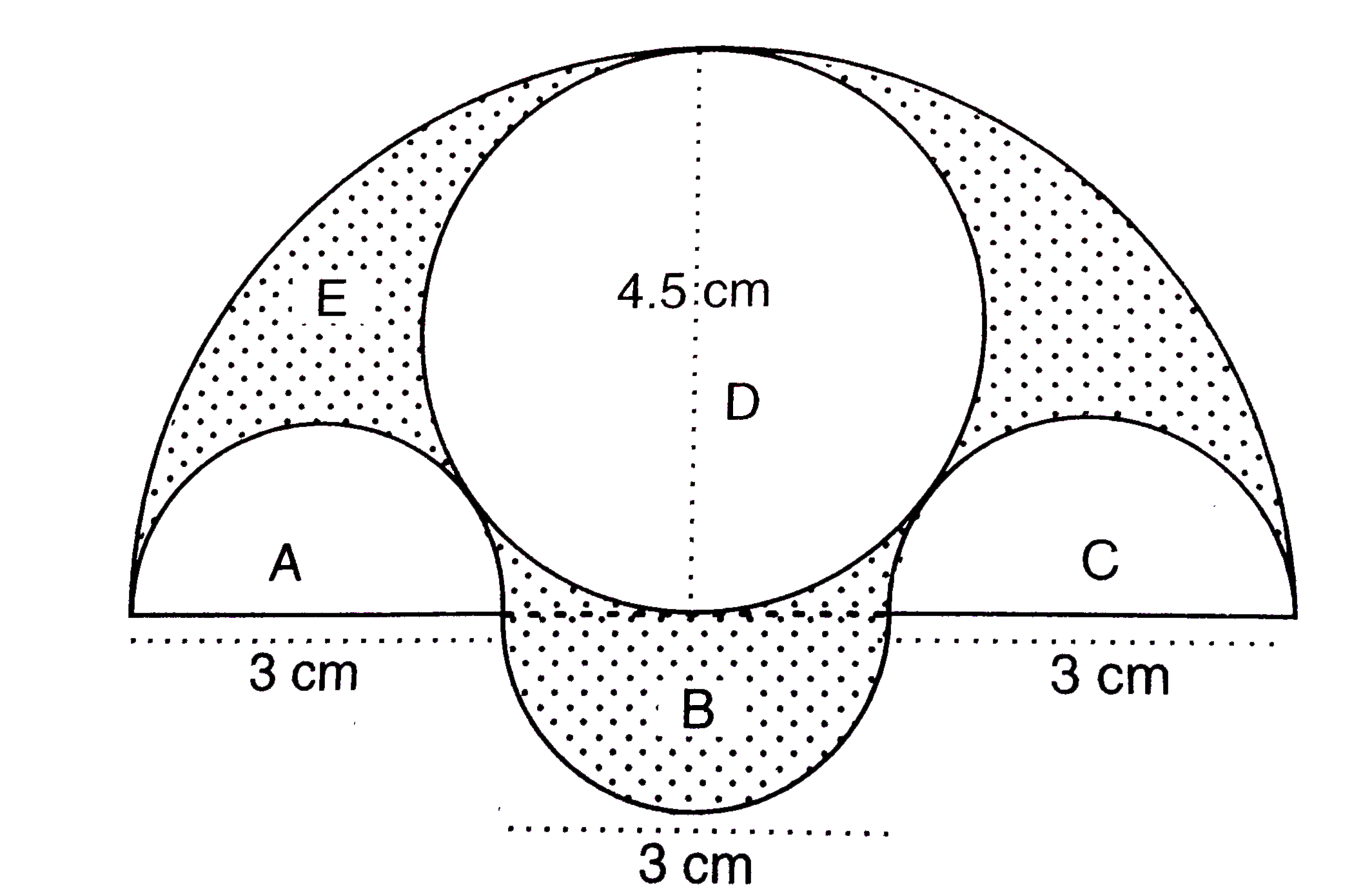
25 पैसे प्रति वर्ग सेमी. की दर से छायांकित भाग की पेन्टिंग लगभग रूपये में |
View Solutionचित्र में, O एक वृत्ताकार चाप का केन्द्र है, तथा AOB एक सरल रेखा है | छायांकित भाग का परिमाप तथा छायांकित भाग का क्षेत्रफल सही एक दशलमव स्थान तक ज्ञात कीजिए | `(pi=3.142" लीजिए")`
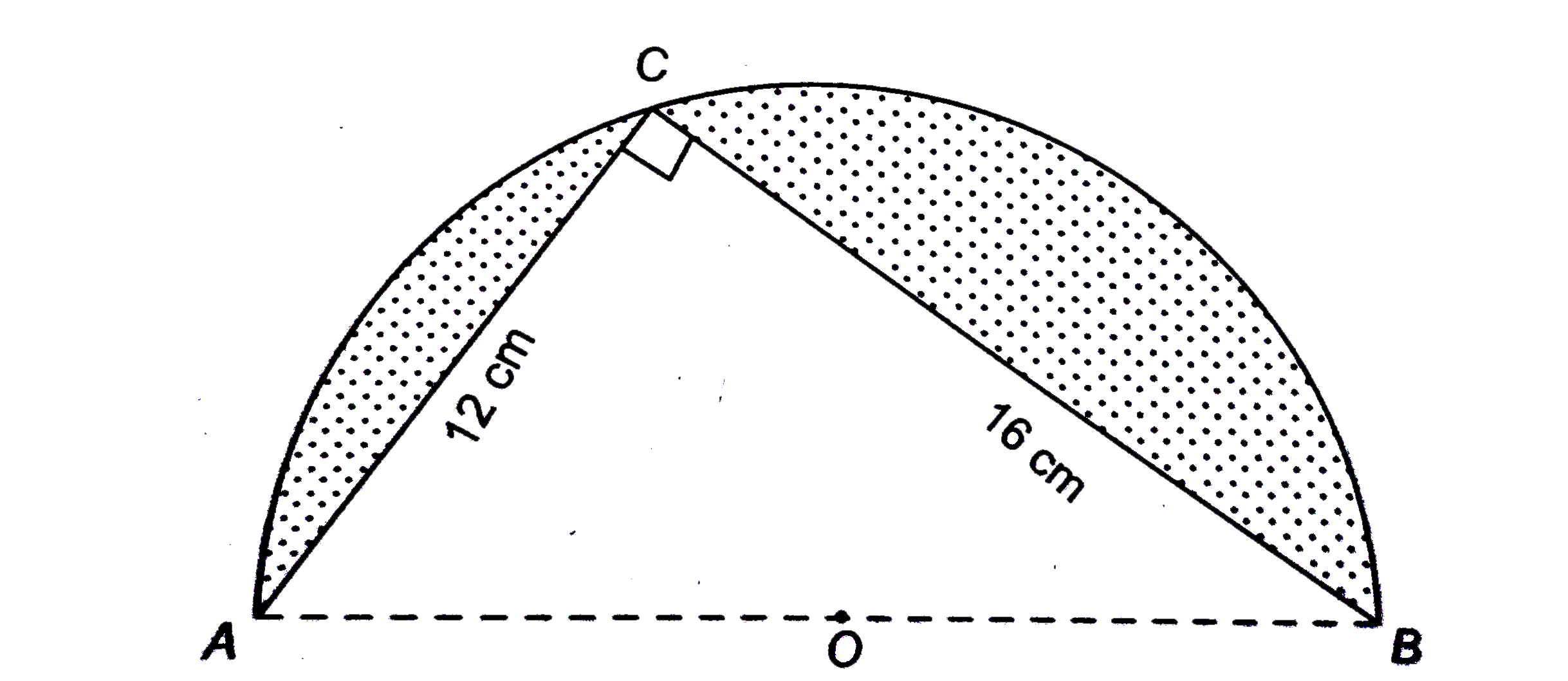
View Solutionचित्र में, ABCD एक 2a भुजा वाला वर्ग है |

अंत: तथा बाह्य वृत्तों की परिधियों का अनुपात ज्ञात कीजिए |
View Solutionचित्र में, ABCD एक 2a भुजा वाला वर्ग है |

अंत: तथा बाह्य वृत्तों के क्षेत्रफलों का अनुपात ज्ञात कीजिए |
View Solutionचित्र में, A तथा B केन्द्रों वाले दो वृत्त एक दूसरे को बिन्दु C पर स्पर्श करते हैं | यदि AC = 8 सेमी. तथा AB = 3 सेमी. हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
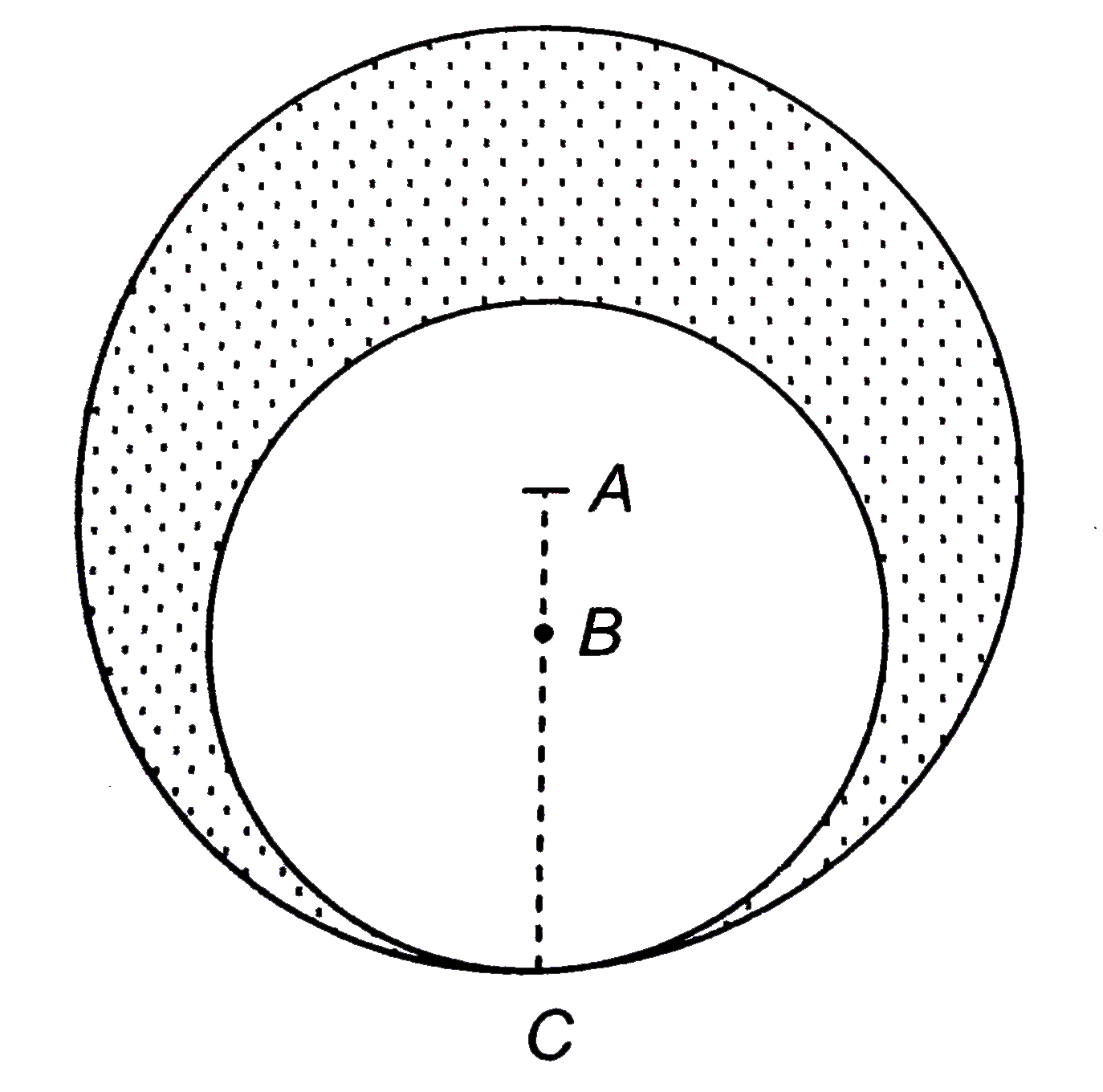
View Solutionचित्र में, ABCD एक आयत है, जहाँ AB = 14 सेमी. तथा BC = 7 सेमी. है | DC, BC तथा AD को व्यास लेकर तीन अर्धवृत्त खींचे गए हैं, जैसा कि चित्र में दर्शाया गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
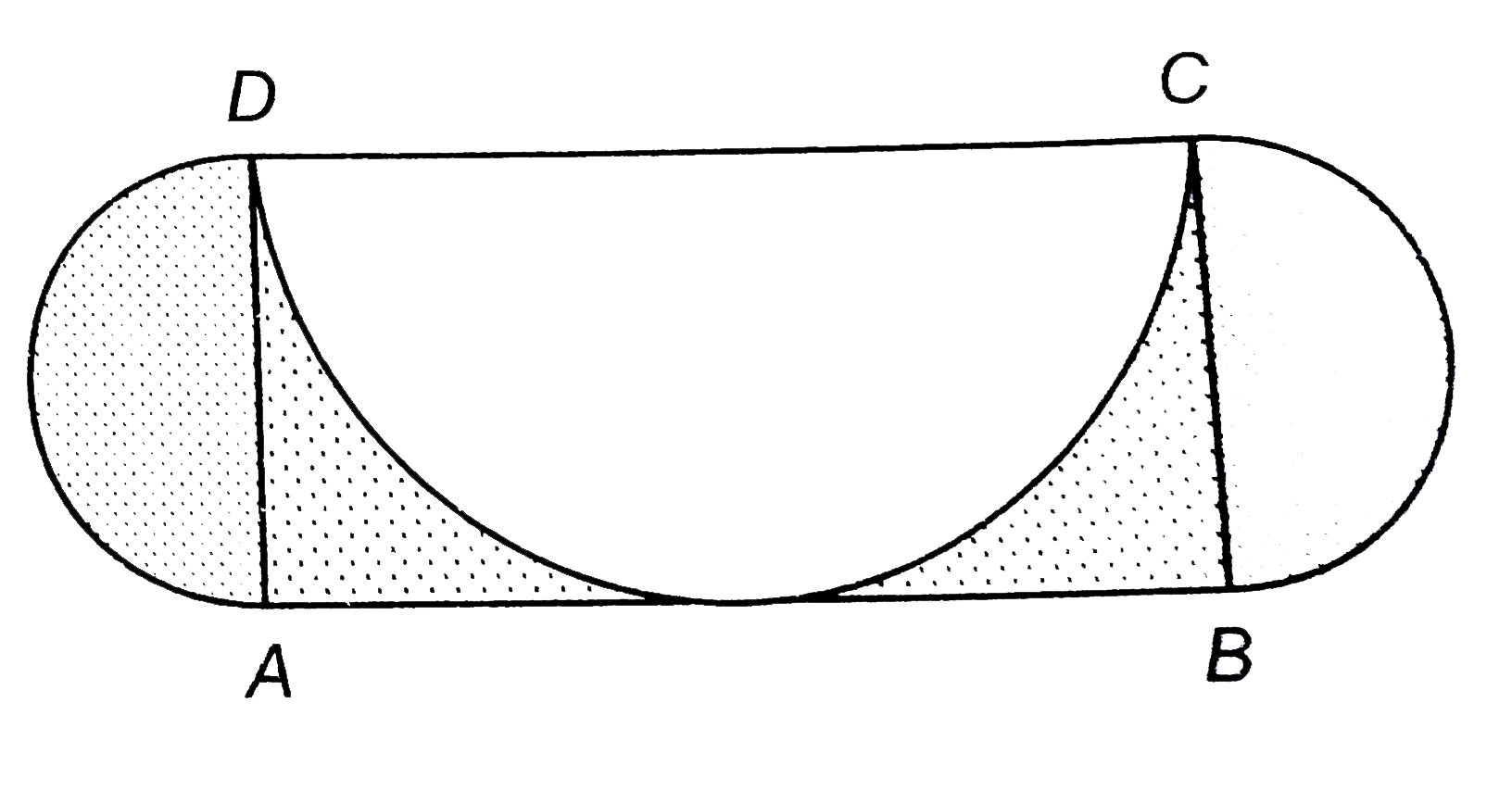
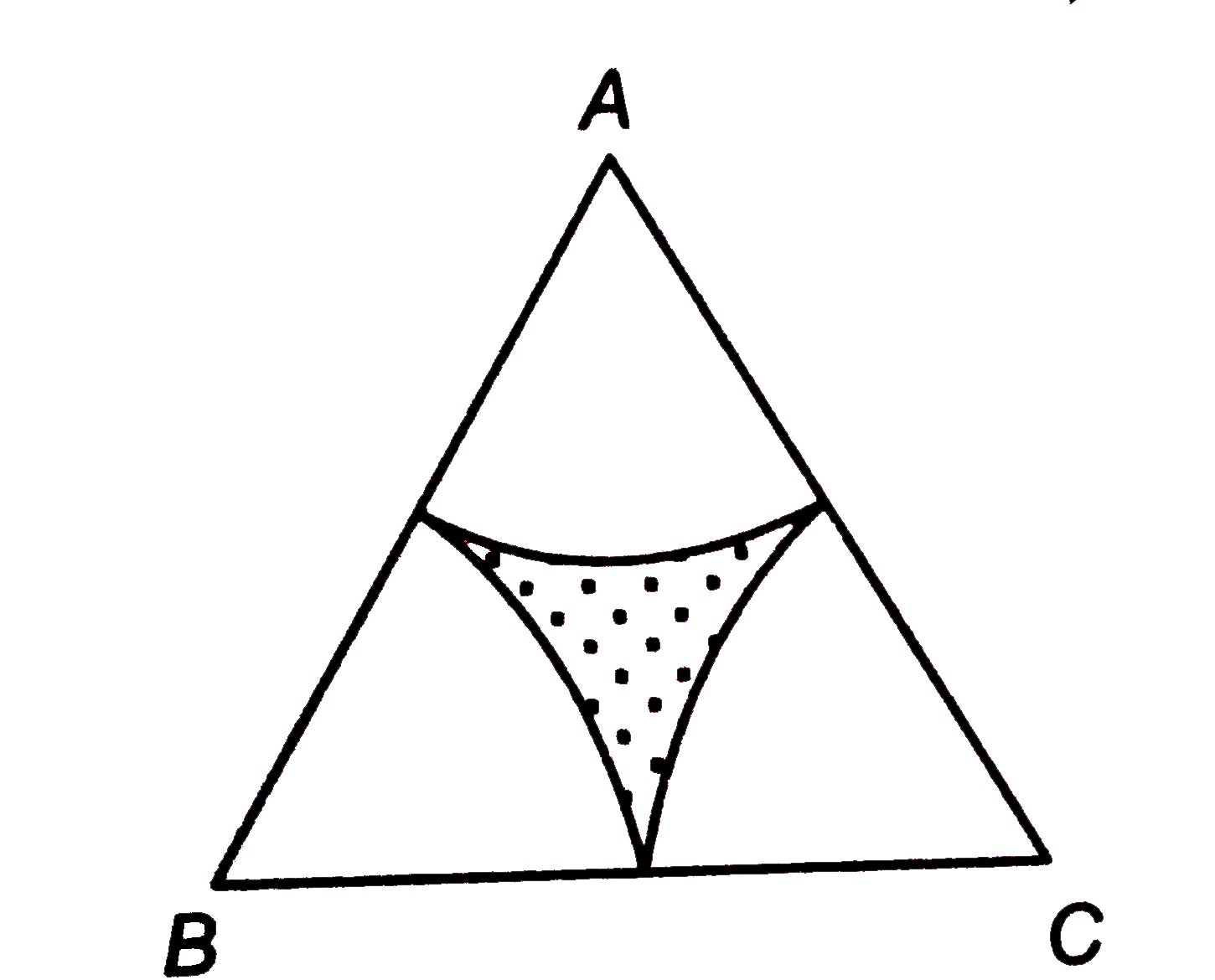
View Solutionचित्र में, ABC एक समबाहु त्रिभुज है, जिसकी प्रत्येक भुजा की लम्बाई 8 सेमी. है | A, B तथा C, 4 सेमी. त्रिज्या वाले वृत्ताकार चापों के केन्द्र हैं | छायांकित भाग का क्षेत्रफल सही दो दशलमव स्थानों तक ज्ञात कीजिए | `(pi=3.142" तथा "sqrt(3)=1.732" लीजिए")`
View Solutionचित्र में, छायांकित भाग की सीमा में चार अर्धवृत्ताकार चापें हैं, जिनमें से सबसे छोटी दो, परस्पर समान हैं | यदि सबसे बड़ी चाप का व्यास 14 सेमी. तथा सबसे छोटी चाप का व्यास 3.5 सेमी. हो, तो :
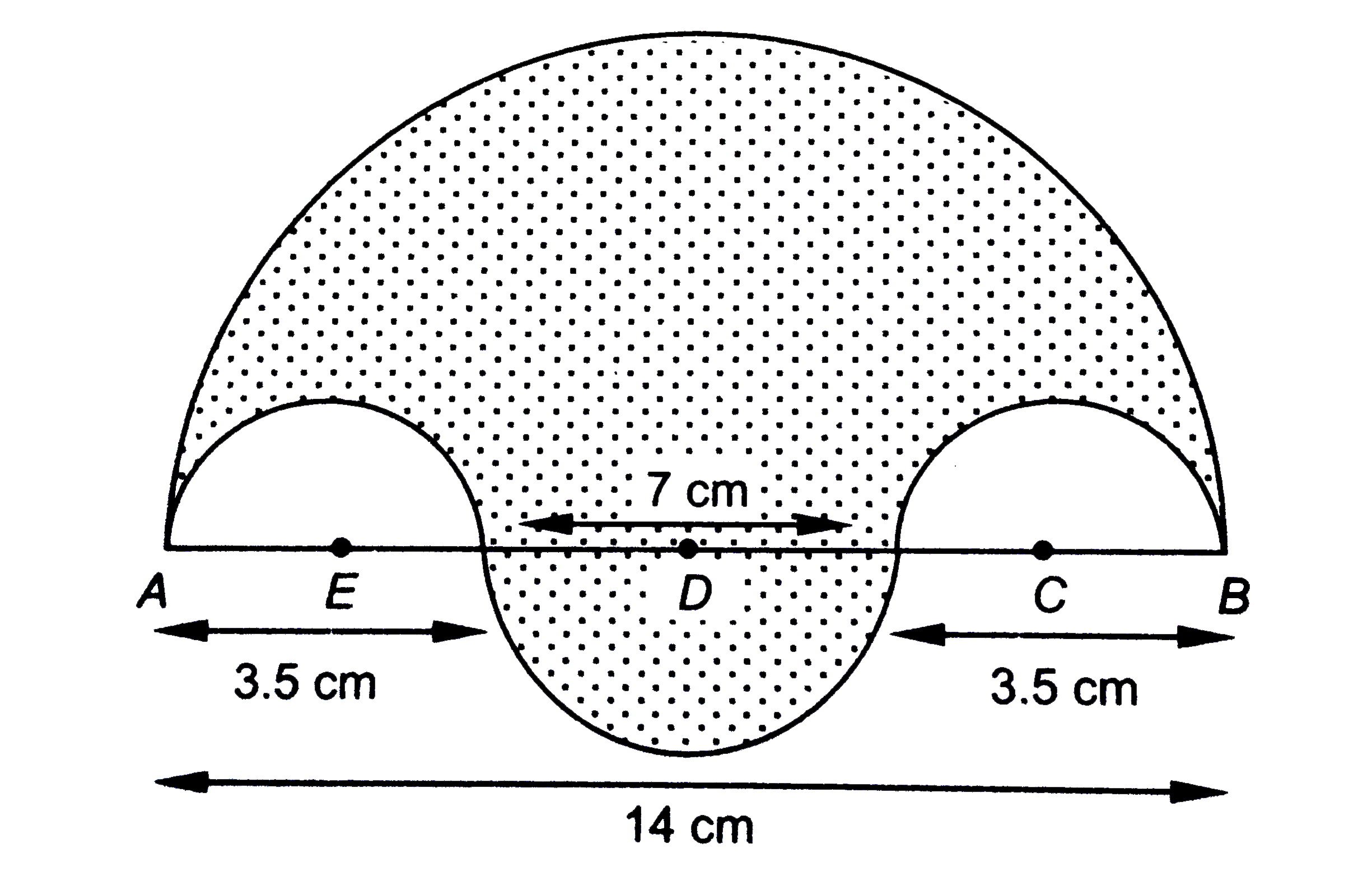
सीमा की लम्बाई ज्ञात कीजिए |
View Solutionचित्र में, छायांकित भाग की सीमा में चार अर्धवृत्ताकार चापें हैं, जिनमें से सबसे छोटी दो, परस्पर समान हैं | यदि सबसे बड़ी चाप का व्यास 14 सेमी. तथा सबसे छोटी चाप का व्यास 3.5 सेमी. हो, तो :

छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
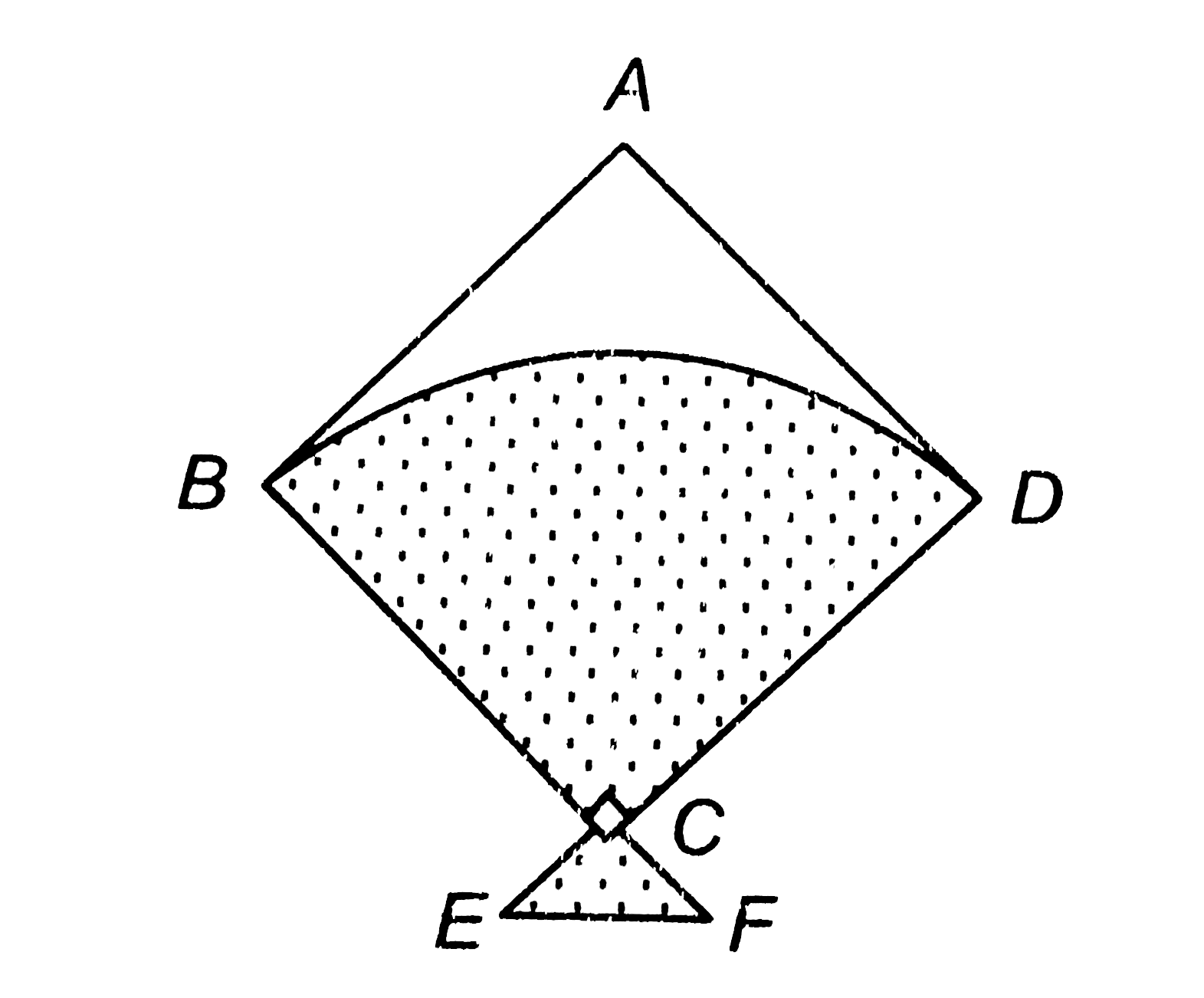
View Solutionचित्र में, एक पतंग दिखाई गई है जिसमें BCD एक 42 सेमी. त्रिज्या वाले वृत्त के चतुर्थांश के आकार का है | ABCD एक वर्ग है तथा CEF एक समद्विबाहु त्रिभुज है जिसकी प्रत्येक भुजा की लम्बाई 6 सेमी. है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
View Solutionचित्र में, AB = 36 सेमी. तथा M,AB का मध्यबिन्दु है | AB, AM तथा MB को व्यास लेकर तीन अर्धवृत्त खींचे गए हैं | केन्द्र C वाला एक वृत्त तीनों अर्धवृत्तों को स्पर्श करता है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, ABC एक समकोण त्रिभुज है जिसमें कोण `A=90^(@)` AB = 21 सेमी. तथा AC = 28 सेमी. है | AB, BC तथा AC को लेकर अर्धवृत्त खींचे गये हैं | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
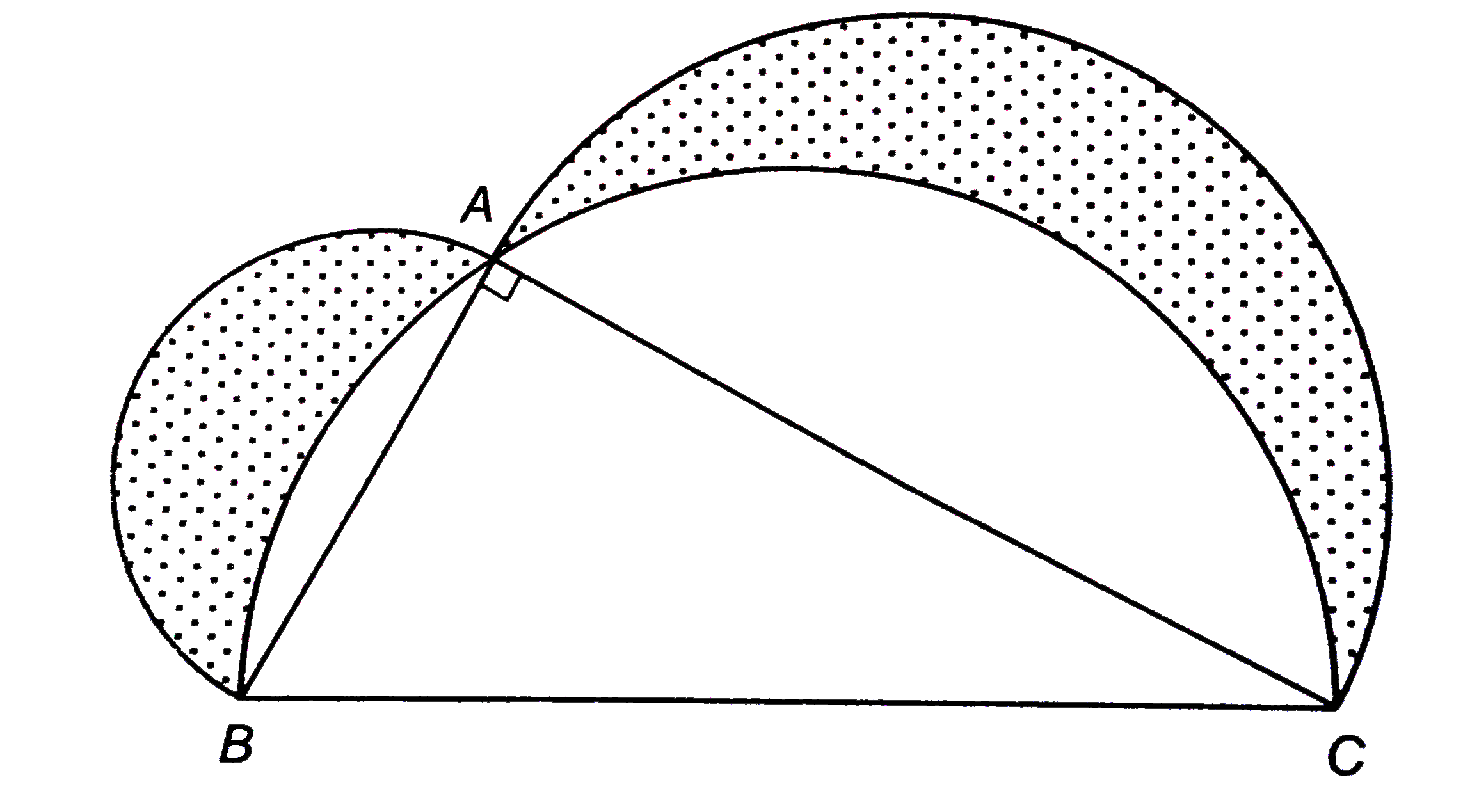
View Solution
पुनरावृत्ति प्रश्नावली questions and complete solutions for chapter वृत्तों से सम्बन्धित क्षेत्रफल of RD SHARMA MATHS (HINDI) of Class 10