Complete Solutions to उदाहरण of chapter वृत्तों से सम्बन्धित क्षेत्रफल of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | वृत्तों से सम्बन्धित क्षेत्रफल |
| RD SHARMA HINDI | उदाहरण |
| Number Of Questions | 85 |
| Academic Year | 2023-24 |
एक 8.4 सेमी. त्रिज्या वाले वृत्त की परिधि एवं क्षेत्रफल ज्ञात कीजिए ?
View Solutionएक वृत्त का क्षेत्रफल ज्ञात कीजिए जिसकी परिधि 22 सेमी. है |
View Solutionएक वृत्त के चतुर्थांश का क्षेत्रफल ज्ञात कीजिये जिसकी परिधि 22 सेमी. है |
View Solutionयदि एक अर्धवृत्ताकार चाँदा की परिधि 66 सेमी. है, तो चाँदा का व्यास ज्ञात कीजिये |
`(pi=22//7)`
View Solutionएक वृत्त की परिधि इसके व्यास से 16.8 सेमी. अधिक है | वृत्त की त्रिज्या ज्ञात कीजिए |
View Solutionदो वृत्त बाह्ययत: स्पर्श करते हैं | यदि इनके क्षेत्रफलों का योग `130pi` वृत्त सेमी. है तथा इनके केंद्रों के बीच की दूरी 14 सेमी. है, तो इन वृत्तों की त्रिज्यायें ज्ञात कीजिए |
View Solutionदो वृत्त अन्त: स्पर्श करते हैं | इनके क्षेत्रफलों का योगफल `116pi` वर्ग सेमी. तथा इनके केन्द्रों के बीच की दूरी 6 सेमी. है | वृत्तों की त्रिज्यायें ज्ञात कीजिए |
View Solutionएक ताँबे के तार को जब एक वर्ग के आकार में मोड़ा जाता है तो इसके द्वारा आन्तरित क्षेत्रफल `484" सेमी."^(2)` है | यदि इसी तार को वृत्त के रूप में मोड़ा जाये तो इसके द्वारा आन्तरित क्षेत्रफल ज्ञात कीजिये ? `(pi=22//7)`
View Solutionएक तार को मोड़कर 28 सेमी. त्रिज्या का एक वृत्त बनाया जा सकता है | यदि इसी तार को एक वर्ग के आकार में मोड़ा जाये, तो वर्ग की भुजा की लम्बाई ज्ञात कीजिए |
View Solutionएक वृत्ताकार ट्रैक की आन्तरिक और बाहय परिधि क्रमश: 352 मी. और 396 मी. हैं | ट्रैक की चौड़ाई ज्ञात कीजिए |
View Solutionएक वृत्ताकार ट्रैक की आन्तरिक परिधि 220 मी. है | यदि ट्रैक की चौड़ाई प्रत्येक स्थान पर 7 मी. हो, तो 2 रु प्रति मीटर की दर से बाहय वृत्त के चारों ओर तार लगाने के खर्च की गणना कीजिये | (दिया है `pi=22//7`)
View Solutionयदि एक साइकिल का पहिया 11 किमी. चलने में 5000 चक्कर लगाता हो, तो पहिये का व्यास ज्ञात कीजिए |
View Solution42 सेमी. त्रिज्या वाले पहिये को 792 मीटर की दूरी तय करने में कितने चक्कर लगाने पड़ेंगे ?
View Solutionएक लड़का इस प्रकार साइकिल चला रहा है कि साइकिल के पहिये प्रति मिनट 140 चक्कर लगाते हैं | यदि पहिये का व्यास 60 सेमी. हो, तो प्रति घण्टा लड़के की चाल ज्ञात कीजिये |
View Solutionएक बस के पहिये का व्यास 140 सेमी. है | यदि बस की चाल 66 किमी. प्रति घण्टा हो, तो पहिये को प्रति मिनट कितने चक्कर लगाने होंगे ?
View Solutionएक कार के प्रत्येक पहिये का व्यास 80 सेमी है | यदि कार 66 किमी प्रति घण्टे की चाल से चल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाता है |
View Solutionएक वृत्ताकार खेत पर 24 रु. प्रति मीटर की दर से बाड़ लगाने का व्यय 5280 रु. आता है | इस खेत की 0.50 रु. प्रति वर्ग मीटर की दर से जुताई करानी हो, तो खेत की जुताई कराने का व्यय ज्ञात कीजिए | (`pi=22//7` लीजिए)
View Solutionचित्र एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केन्द्र से बाहर की ओर पाँच क्षेत्र Gold, Red, Blue Black तथा White चिन्हित हैं, जिनसे अंक अर्जित किये जा सकते हैं | Gold अंक वाले क्षेत्र का व्यास 21 सेमी. है | तथा प्रत्येक अन्य पटटी 10.5 सेमी. चौड़ी है | अंक प्राप्त कराने वाले पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए |

View Solution21 सेमी. त्रिज्या के वृत्त से `150^(@)` कोण वाला त्रिज्यखण्ड काटा गया है | त्रिज्यखण्ड की संगत चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिये |
View Solutionउस वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिये जिसकी त्रिज्या 14 सेमी. तथा त्रिज्यखण्ड का कोण `45^(@)` है | (दिया है `pi=22//7`)
View Solutionचित्र में, 7 सेमी. ओर 3.5 सेमी. त्रिज्याओं वाले दो संकेन्द्रीय वृत्तों के त्रिज्यखण्ड प्रदर्शित किये गये हैं | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | `(pi=22//7)`
View Solutionयदि एक पेंडुलम `30^(@)` के कोण पर घूमते हुये 8.8 सेमी. लम्बाई का चाप बनाता हो, तो पैंडुलम कि लम्बाई ज्ञात कीजिए `(pi=22//7)`
View Solutionएक घड़ी की मिनट की सुई की लम्बाई 14 सेमी. है | सुई द्वारा एक मिनट में बुहार किया गया क्षेत्रफल ज्ञात कीजिये | `(pi=22//7)`
View Solution5.2 सेमी. त्रिज्या वाले वृत्त के एक त्रिज्यखण्ड का परिमाप 16.4 सेमी. हो, तो त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिये |
View Solutionएक घड़ी की मिनट की सुई 10 सेमी. लम्बी है | मिनट की सुई द्वारा प्रात: 9 बजे से 9.35 बजे तक बुहार किया गया क्षेत्रफल ज्ञात कीजिये |
View Solutionएक घड़ी की छोटी तथा लम्बी सुईयाँ क्रमश: 4 सेमी. तथा 6 सेमी. लम्बी हैं | सुईयों की नोकों द्वारा 2 दिन में चली गयी दूरियों का योगफल ज्ञात कीजिये | `(pi=22//7)`
View Solution4 सेमी. त्रिज्या वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका कोण `30^(@)` है | इसके संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल भी ज्ञात कीजिए | `(pi=3.14)`
View Solutionएक 5 सेमी त्रिज्या वाली पुली के चारों ओर लचीली बेल्ट चढ़ायी जाती है | बेल्ट के एक बिन्दु को पुली के केन्द्र O से सीधा P बिन्दु तक 10 सेमी तक खिंचा जाता है | पुली की रिम पर बचे हुए बेल्ट की लम्बाई ज्ञात कीजिए तथा छायांकित भाग का क्षेत्रफल भी ज्ञात कीजिए |
View Solutionएक वृत्त के चाप की लम्बाई `5pi` है तथा त्रिज्यखण्ड `20pi` वर्ग सेमी के क्षेत्रफल से घिरा है | वृत्त की त्रिज्या ज्ञात कीजिए |
View SolutionO केन्द्र वाले वृत्त की त्रिज्या 5 सेमी. तथा जीवा AB की लम्बाई `5sqrt(3)` सेमी. है | त्रिज्यखण्ड AOB का क्षेत्रफल ज्ञात कीजिए |
View Solutionकिसी कार के दो वाइपर जो एक दूसरे पर कभी आच्छादित नहीं होते हैं | प्रत्येक वाइपर की पत्ती की लम्बाई 25 सेमी है और `115^(@)` के कोण तक घूम कर सफाई कर सकता है | पत्तियों के प्रत्येक बुहार के साथ साफ किये गये क्षेत्र का क्षेत्रफल ज्ञात कीजिए |
View Solutionजहाजों को समुद्र में जलस्तर के निचे स्थित चटटानों की चेतावनी देने के लिए, एक लाइट हाउस `80^(@)` कोण वाले एक त्रिज्यखण्ड में 16.5 किमी. की दूरी तक लाल रंग का प्रकाश फैलाता है | समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाजों को चेतावनी दी जा सके | (दिया है : `pi=3.14`) |
View Solutionएक छतरी में आठ तानें हैं, जो बराबर दूरी पर लगी हुए हैं | छतरी को 45 सेमी. त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल बताइए |
View Solutionएक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी. है | तार को वृत्त के 5 व्यासों को बनाने में भी प्रयोग किया गया है जो वृत्त को 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा की चित्र में दिखाया गया है | तो ज्ञात कीजिए कि:

कुल वांछित चाँदी के तार की लम्बाई
View Solutionएक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी. है | तार को वृत्त के 5 व्यासों को बनाने में भी प्रयोग किया गया है जो वृत्त को 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा की चित्र में दिखाया गया है | तो ज्ञात कीजिए कि:

ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल
View Solutionयदि एक त्रिज्यखण्ड का कोण `120^(@)` तथा वृत्त की त्रिज्या 21 सेमी. हो, तो वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिये | (दिया है: `pi=22//7`)
View Solutionयदि 10 सेमी. त्रिज्या के वृत्त में एक जीवा AB वृत्त के केन्द्र पर समकोण बनाती हो, तो लघु तथा दीर्ध वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिये | (दिया है : `pi=3.14`)
View Solutionएक 15 सेमी. त्रिज्या वाले वृत्त की एक जीवा AB, वृत्त के केन्द्र पर `60^(@)` का कोण बनाती हो, तो दीर्ध तथा लघु वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिये | (माना : `pi=3.14,sqrt(3)=1.73`)
View Solutionएक 21 सेमी. त्रिज्या वाले वृत्त का एक चाप केन्द्र पर `60^(@)` का कोण आन्तरित है | ज्ञात कीजिए :
चाप की लम्बाई
View Solutionएक 21 सेमी. त्रिज्या वाले वृत्त का एक चाप केन्द्र पर `60^(@)` का कोण आन्तरित है | ज्ञात कीजिए :
चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल
View Solutionएक 21 सेमी. त्रिज्या वाले वृत्त का एक चाप केन्द्र पर `60^(@)` का कोण आन्तरित है | ज्ञात कीजिए :
चाप की संगत जीवा द्वारा बने वृत्तखण्ड का क्षेत्रफल |
View Solutionएक 10 सेमी. त्रिज्या के वृत्त में एक जीवा केन्द्र पर समकोण बनाती है | ज्ञात कीजिए:
लघु त्रिज्यखण्ड का क्षेत्रफल
View Solutionएक 10 सेमी. त्रिज्या के वृत्त में एक जीवा केन्द्र पर समकोण बनाती है | ज्ञात कीजिए:
लघु वृत्तखण्ड का क्षेत्रफल
View Solutionएक 10 सेमी. त्रिज्या के वृत्त में एक जीवा केन्द्र पर समकोण बनाती है | ज्ञात कीजिए:
दीर्ध त्रिज्यखण्ड का क्षेत्रफल
View Solutionएक 10 सेमी. त्रिज्या के वृत्त में एक जीवा केन्द्र पर समकोण बनाती है | ज्ञात कीजिए:
दीर्घ वृत्तखण्ड का क्षेत्रफल
View Solutionचित्र में, PAQ और PBQ दो अलग-अलग वृत्तों की चाप हैं | केन्द्र O तथा त्रिज्या OP वाले वृत्त का एक हिस्सा चाप PAQ है तथा केन्द्र M तथा त्रिज्या OM वाले वृत्त का एक हिस्सा चाप PBQ है जहाँ PQ का मध्य बिन्दु M है | दर्शाइए कि दोनों चापों के द्वारा घिरे हुए भाग का क्षेत्रफल `25(sqrt(3)-(pi)/(6))" सेमी"^(2)` है |

View Solutionएक 40 सेमी. भुजा वाले वर्गाकार धातु की चादर से बने नाली के एक ढक्कन में 1 सेमी. व्यास के 441 छेद हैं | शेष बची धातु की चादर का क्षेत्रफल ज्ञात कीजिए |
View Solutionएक डार्टबोर्ड की प्रथम रिंग के अन्त: तथा बाहय व्यास क्रमश: 32 सेमी. तथा 34 सेमी. और दूसरी रिंग के अन्त: तथा बाहय व्यास क्रमश: 19 सेमी, तथा 21 सेमी. हैं | इन दोनों रिंगों का कुल क्षेत्रफल कितना है ?
View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ज्ञात कीजिए | यदि केन्द्र O पर संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी. तथा 14 सेमी तथा `angleAOC=40^(@)` है |

View Solutionकेन्द्र O पर दो संकेन्द्रिय वृत्तों की त्रिज्याएँ क्रमश: 21 सेमी. तथा 7 सेमी. एवं दो चाप क्रमश: AB तथा CD हैं | यदि `angleAOB=30^(@)` हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
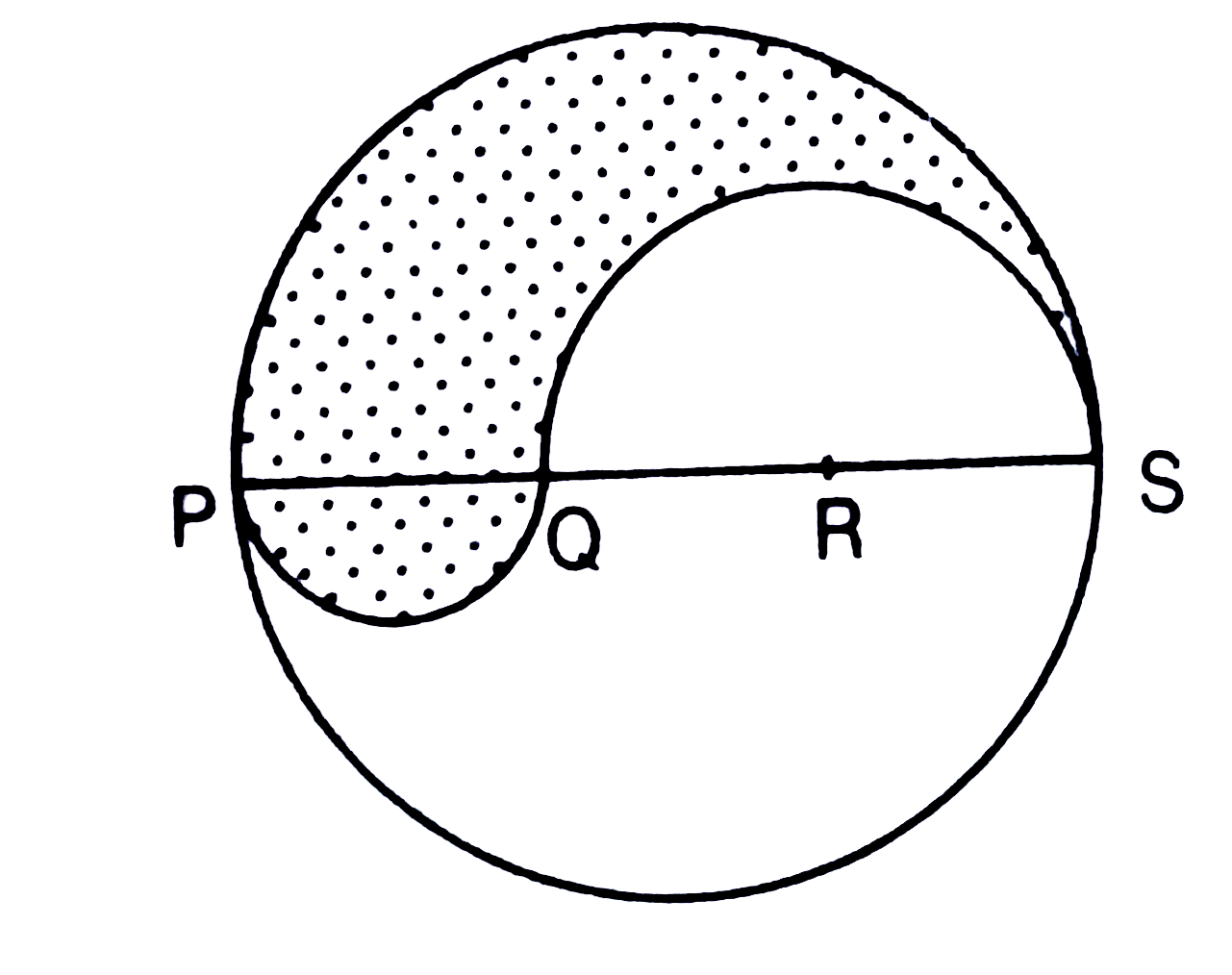
View Solutionएक 6 सेमी. त्रिज्या के वृत्त का व्यास PQRS इस प्रकार है कि PQ, QR और RS बराबर हैं | चित्र के अनुसार PQ और QS को व्यास मानकर अर्धवृत्त खींचे गये हैं | छायांकित भाग का परिमाप तथा क्षेत्रफल ज्ञात कीजिये |
View Solutionएक 70 मी. `xx` 52 मी. माप के आयताकार मैदान के कोने में एक घोड़े को 21 मी. लम्बी रस्सी से घास चरने के लिये बाँधा गया है | वह कितने क्षेत्रफल में घास चर सकता है ?
View Solutionएक कागज आयत ABCD के आकार का है जिसमें AB = 20 सेमी. तथा BC = 14 सेमी है | यदि इसमें से BC व्यास का एक अर्ध वृत्ताकार भाग काट लिया जाता है, तो शेष भाग का क्षेत्रफल ज्ञात कीजिए |
View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | `(pi=3.14)`

View Solutionचित्र में, केन्द्र O तथा 3.5 सेमी. त्रिज्या वाले वृत्त का चतुर्थांश AOBCA है | छायांकित भाग के क्षेत्रफल की गणना कीजिये (दिया है : `pi=22//7`)

View Solutionएक 42 मी. व्यास के वृत्ताकार घास के मैदान के बाहर चारों ओर 3.5 मी. चौड़ा रास्ता है | रास्ते में 4 रु प्रति वर्ग मी. की दर से कंकड़ बिछवाने का खर्च ज्ञात कीजिए |
View Solutionएक वर्गाकार पार्क की प्रत्येक भुजा 100 मी. है | पार्क के प्रत्येक कोने पर 14 मी. त्रिज्या के वृत्त के चतुर्थांश के आकार की फूलों की क्यारियाँ हैं जैसा चित्र में दिखाया गया है | पार्क के शेष भाग का क्षेत्रफल ज्ञात कीजिये | (दिया है : `pi=22//7`)
View Solutionएक वर्ग के चारों कोनों पर चार बराबर वृत्त इस प्रकार बनाये गये हैं कि प्रत्येक वृत्त अन्य दो को स्पर्श करता है जैसा कि चित्र में प्रदर्शित किया गया है | यदि वर्ग की प्रत्येक भुजा की माप 14 सेमी. हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
View Solutionउस वृत्त की त्रिज्या दशमलव के तीन स्थानों तक ज्ञात कीजिये जिसका क्षेत्रफल उन त्रिभुजों के क्षेत्रफलों के योगफल के बराबर है जिनकी भुजायें सेंटीमीटर में 35, 53, 66 तथा 33, 56 तथा 65 हैं | (दिया है: `pi=22//7`)
View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
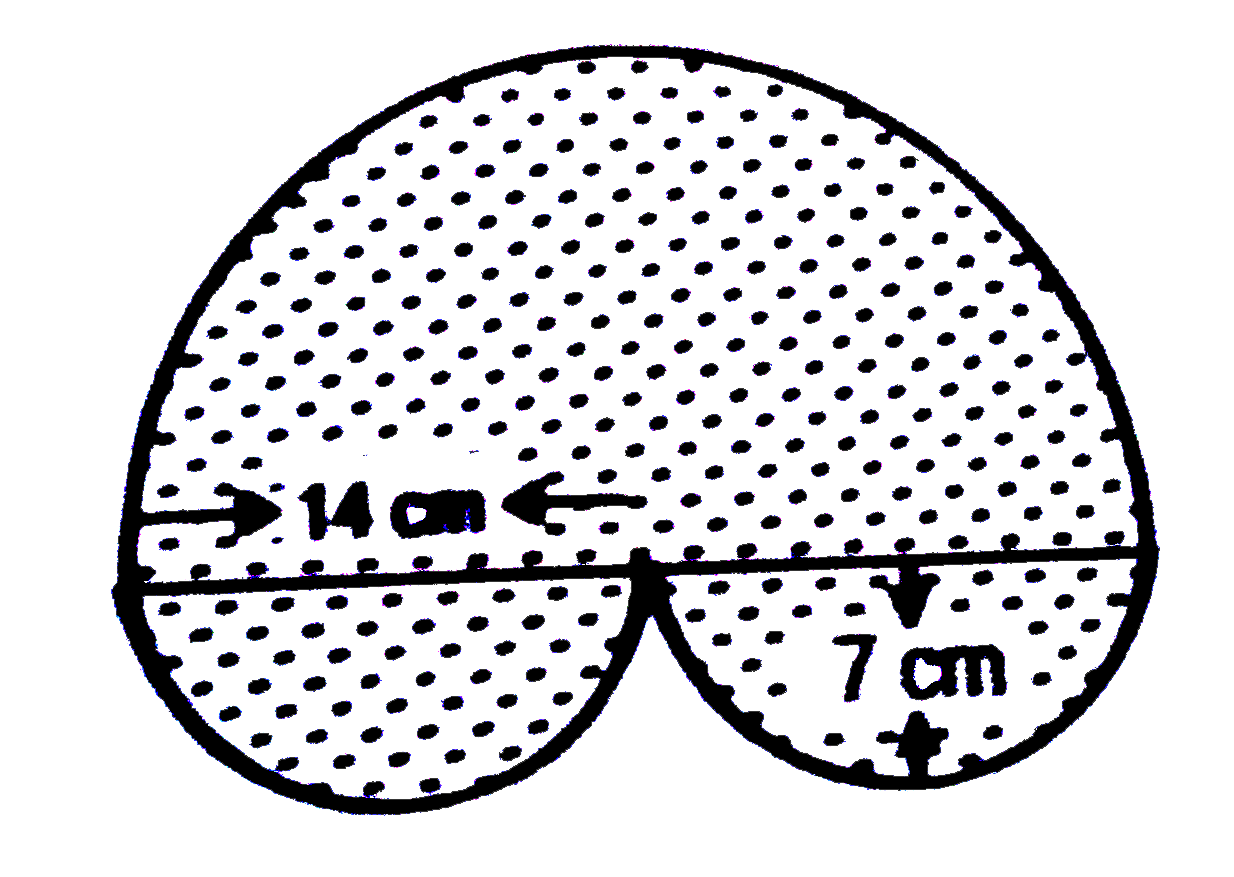
View Solution24 सेमी. भुजा वाले एक समबाहु त्रिभुज में, इसकी भुजाओं को स्पर्श करता हुआ एक अन्त:वृत्त बनाया गया है | त्रिभुज के शेष भाग का क्षेत्रफल ज्ञात कीजिये | (दिया है : `sqrt(3)=1.732`)
View Solutionएक 14 मी. दौड़ने का पथ दो 120 मी. लम्बे सीधे भागों तथा दो 35 मी. आन्तरिक त्रिज्या वाले अर्धवृत्ताकार भागों से मिलकर बना है | छायांकित भाग के क्षेत्रफल की गणना कीजिए |
View SolutionABCD एक फूलों की क्यारी है | यदि OA = 21 मी. तथा OC = 14 मी. हो, तो क्यारी का क्षेत्रफल ज्ञात कीजिये | `(pi=22//7)`
View SolutionABCP एक 14 सेमी. त्रिज्या वाले वृत्त का चतुर्थांश है | AC को व्यास मानकर एक अर्धवृत्त खींचा गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिये |
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल `49sqrt(3)" सेमी."^(2)` है | प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा की लम्बाई की आधी त्रिज्या लेकर वृत्त खींचे गये हैं जैसा कि चित्र में प्रदर्शित किया गया है | त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिये जो वृत्तों में सम्मिलित नहीं है |
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल `1732.05" सेमी."^(2)` है | इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर, त्रिभुज की भुजा की लम्बाई के आधे के बराबर त्रिज्या लेकर वृत्त खींचे गये हैं | त्रिभुज का वह क्षेत्रफल ज्ञात कीजिये जो वृत्तों में सम्मिलित नहीं हैं | `(pi=3.14)`
View Solutionएक 58 मी. भुजा वाले वर्गाकार घास के मैदान के सिरों पर दो वृत्ताकार भाग जोड़ने का प्रस्ताव है | प्रत्येक वृत्त का केन्द्र वर्ग के विकर्णो का प्रतिच्छेद बिन्दु है | पूरे मैदान का क्षेत्रफल ज्ञात कीजिये |
View Solutionचित्र में, एक 56 मीटर भुजा वाले वर्गाकार लॉन ABCD के दोनों ओर बनी हुई दो वृत्ताकार फूलों की क्यारियाँ दिखाई गयी हैं | यदि प्रत्येक वृत्ताकार क्यारी का केन्द्र लॉन के विकर्णों का प्रतिच्छेद बिन्दु O हो, तो वर्गाकार लॉन तथा फूलों की क्यारियों के क्षेत्रफलों का योग ज्ञात कीजिए |
View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए जहाँ ABCD भुजा 10 सेमी. का वर्ग है तथा इस वर्ग की प्रत्येक भुजा को व्यास मानकर अर्धवृत्त खींचे गए हैं | `(pi=3.14)`
View Solutionयदि ABCD 14 सेमी. भुजा का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं, तो चित्र में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
View SolutionABCD एक समलम्ब चतुर्भुजाकार मैदान है | जिसमें `"AB"||"DC", angleABC=90^(@)` और `angleDAB=60^(@)` है | शीर्षों A, B, C और D के केन्द्र लेकर चार त्रिज्यखण्ड बनाये गये हैं जैसा की चित्र में दिखाया गया है | यदि प्रत्येक त्रिज्यखण्ड की त्रिज्या 17.5 मीटर है, तो ज्ञात कीजिए :
चारों त्रिज्यखण्डों का कुल क्षेत्रफल |
View SolutionABCD एक समलम्ब चतुर्भुजाकार मैदान है | जिसमें `"AB"||"DC", angleABC=90^(@)` और `angleDAB=60^(@)` है | शीर्षों A, B, C और D के केन्द्र लेकर चार त्रिज्यखण्ड बनाये गये हैं जैसा की चित्र में दिखाया गया है | यदि प्रत्येक त्रिज्यखण्ड की त्रिज्या 17.5 मीटर है, तो ज्ञात कीजिए :
मैदान के बचे हुए शेष भाग का क्षेत्रफल जबकि AB = 75 मीटर तथा CD = 50 मीटर दिया है |
View Solutionएक गोल मेजपोश पर 6 बराबर डिजाइन बने हुए हैं जैसा कि चित्र में दिखाया गया है | यदि मेजपोश कि त्रिज्या 28 सेमी हो, तो 3.50 रूपये प्रति वर्ग सेमी. की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए | `(sqrt(3)=1.7" का प्रयोग कीजिए |")`

View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए जहाँ 12 सेमी. भुजा वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मानकर 6 सेमी त्रिज्या का एक वृत्ताकार चाप खींचा गया है |

View Solutionएक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, के बिच में एक समबाहु त्रिभुज ABC को छोड़ते हुए एक डिजाइन बना हुआ है, जैसा कि चित्र में दिखाया गया है | इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, AB और CD केन्द्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास हैं तथा OD छोटे वृत्त का व्यास है | यदि OA = 7 सेमी हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 सेमी. त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है |

View Solutionचित्र में प्रदर्शित एक वर्गाकार रुमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें प्रत्येक की त्रिज्या 7 सेमी. है | रुमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी., PR = 7 सेमी. तथा O वृत्त का केन्द्र है |
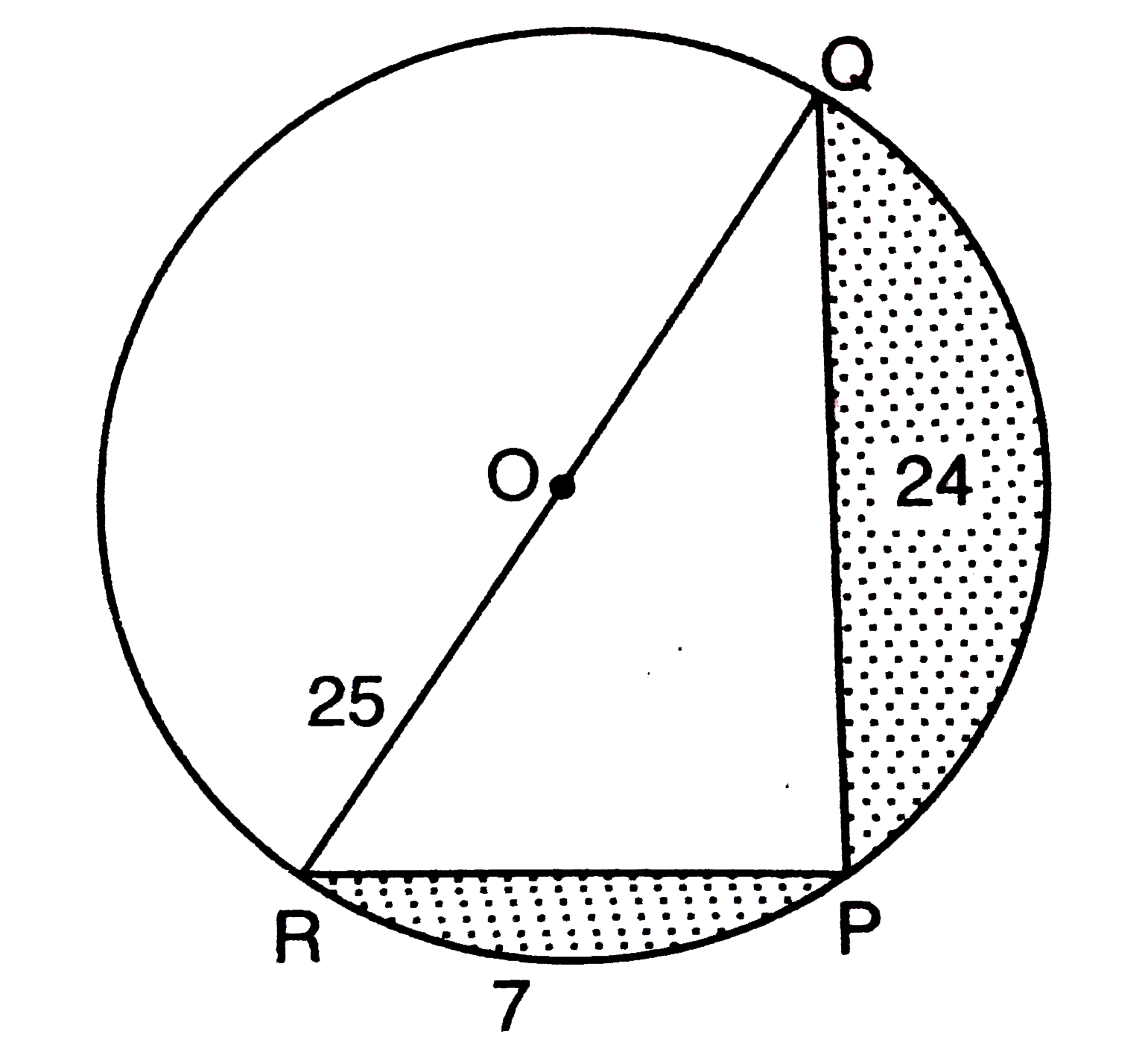
View Solutionचित्र में दो वृत्तों के A बिन्दु पर स्पर्श होने पर एक अर्धचन्द्र बनता है | बिन्दु C बड़े वृत्त का केन्द्र है | BD पर अर्धचन्द्र की चौड़ाई 9 सेमी. तथा EF पर चौड़ाई 5 सेमी. है, तो
(i) दोनों वृत्तों की त्रिज्याओं तथा

View Solutionचित्र में दो वृत्तों के A बिन्दु पर स्पर्श होने पर एक अर्धचन्द्र बनता है | बिन्दु C बड़े वृत्त का केन्द्र है | BD पर अर्धचन्द्र की चौड़ाई 9 सेमी. तथा EF पर चौड़ाई 5 सेमी. है, तो
छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

View Solutionचित्र में, 2 सेमी. त्रिज्या वाले तीन वृत्त एक दूसरे को बाह्यत: स्पर्श करते हैं | इन वृत्तों को एक R सेमी. त्रिज्या वाले दूसरे वृत्त के अन्दर रखा गया है | R का मान तथा छायांकित भाग का क्षेत्रफल `pi` तथा `sqrt(3)` के संदर्भ में ज्ञात कीजिए |

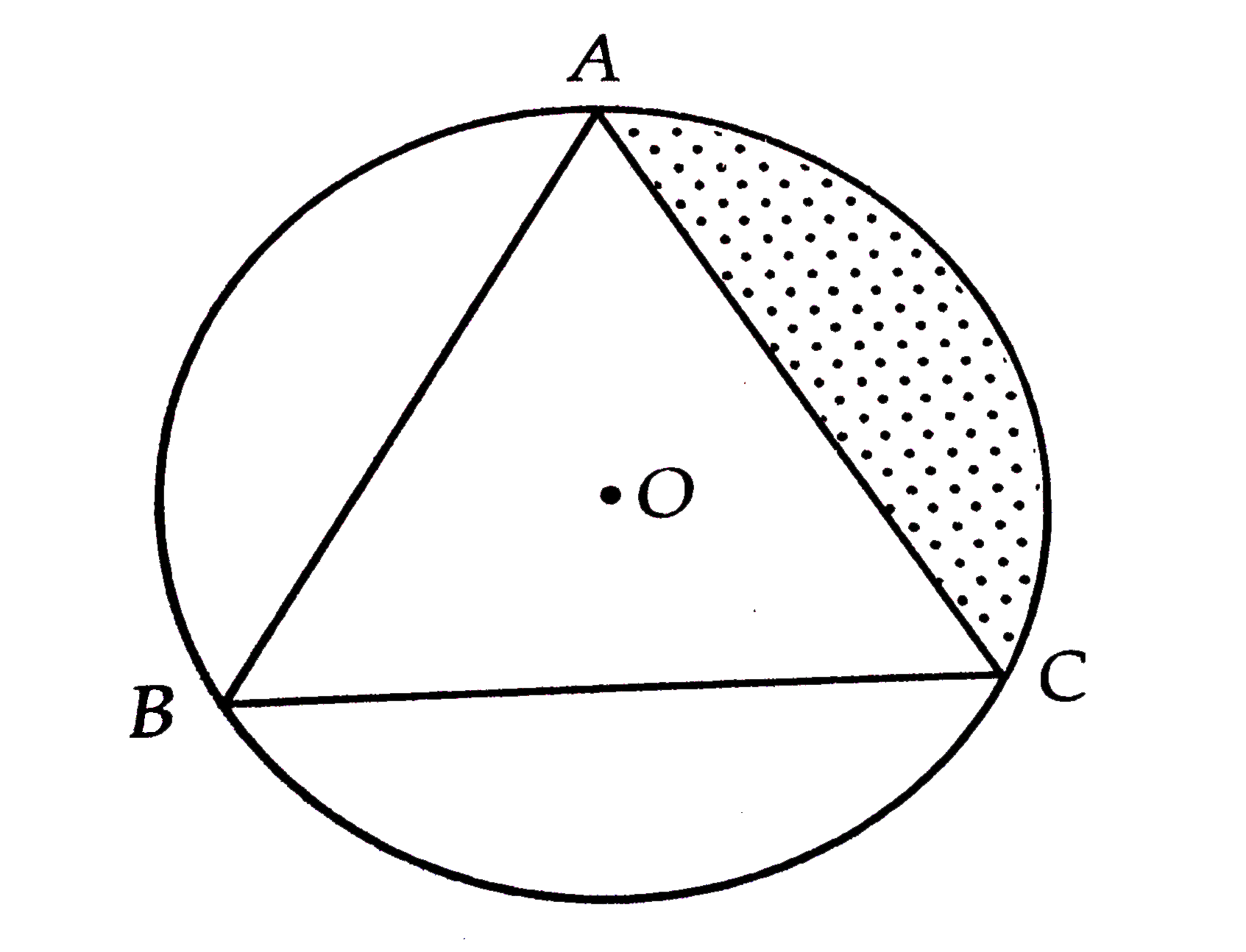
View Solutionचित्र में, केन्द्र O तथा 4 सेमी. त्रिज्या वाले वृत्त के अन्दर एक समबाहु त्रिभुज ABC बनाया गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
View Solutionसंलग्न चित्र में, त्रिभुज ABC शीर्ष बिन्दु A पर एक समकोण त्रिभुज है | जहाँ AB = 6 सेमी., BC = 10 सेमी. तथा `I, DeltaABC` के अन्त:वृत्त का केन्द्र है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |
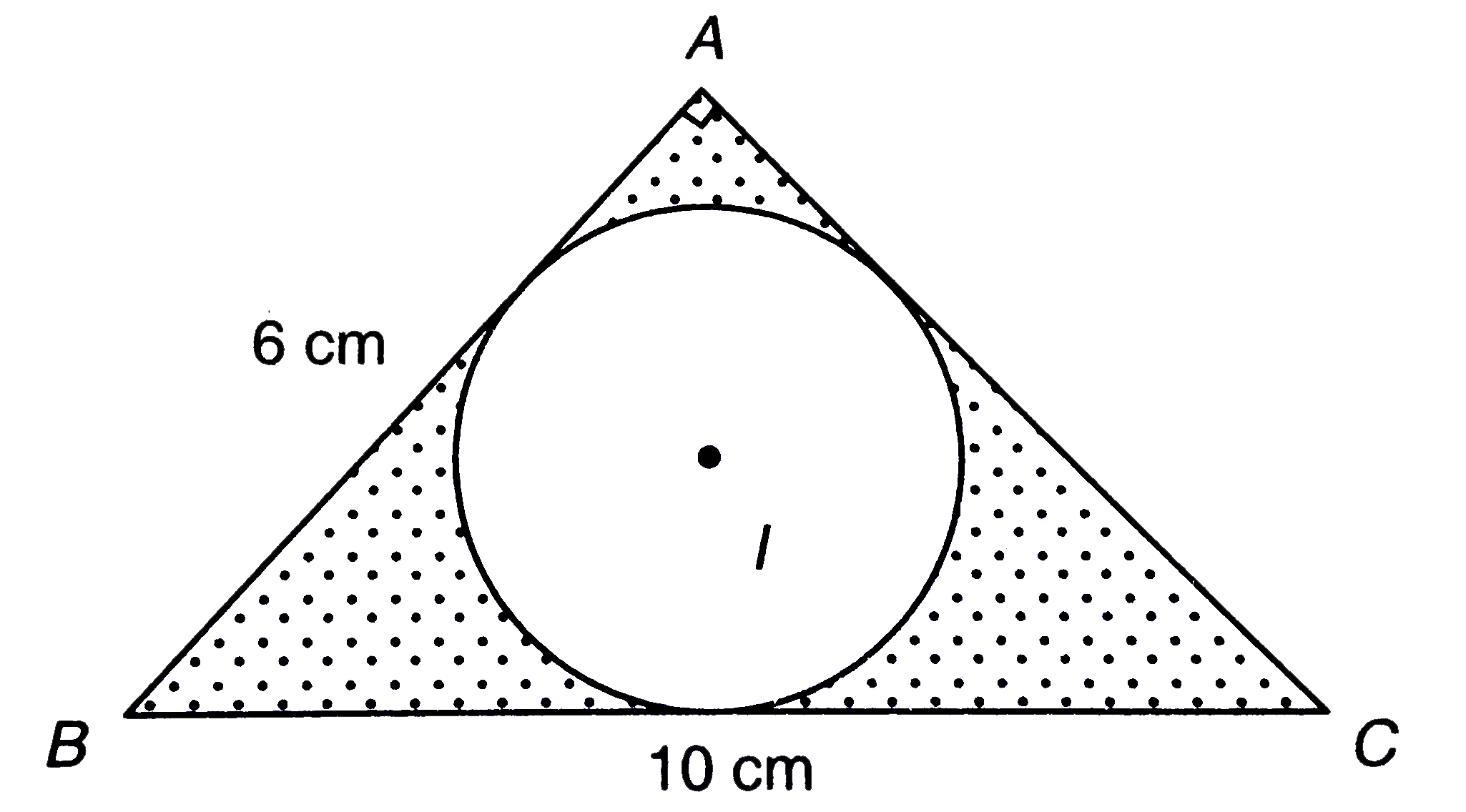
View Solutionचित्र में, ABCD एक समलम्ब चतुर्भुज है, जहाँ `"AB"||"DC"` तथा `angleBCD=60^(@)` है | यदि BFEC केन्द्र C वाले वृत्त का त्रिज्यखण्ड है और AB = BC = 7 सेमी. तथा DE = 4 सेमी. हो, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | `(pi=(22)/(7)" तथा "sqrt(3)=1.732" का प्रयोग कीजिए")`

View Solution
उदाहरण questions and complete solutions for chapter वृत्तों से सम्बन्धित क्षेत्रफल of RD SHARMA MATHS (HINDI) of Class 10