Complete Solutions to Exercise 8A of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| RS AGGARWAL | Exercise 8A |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
A point `P` is at a distance of `29cm` from the centre of a circle of radius `20cm`. Find the length of the tangent drawn from `P` to the circle.
View SolutionA point `P` is `25cm` away from the centre of a circle and the lens of tangent drawn from `P` to the circle is `24cm`. Find the radius.
View SolutionTwo concentric circles are of radii `6.5cm` and `2.5cm`. Find the length of the chord of the larger circle which touches the smaller circle.
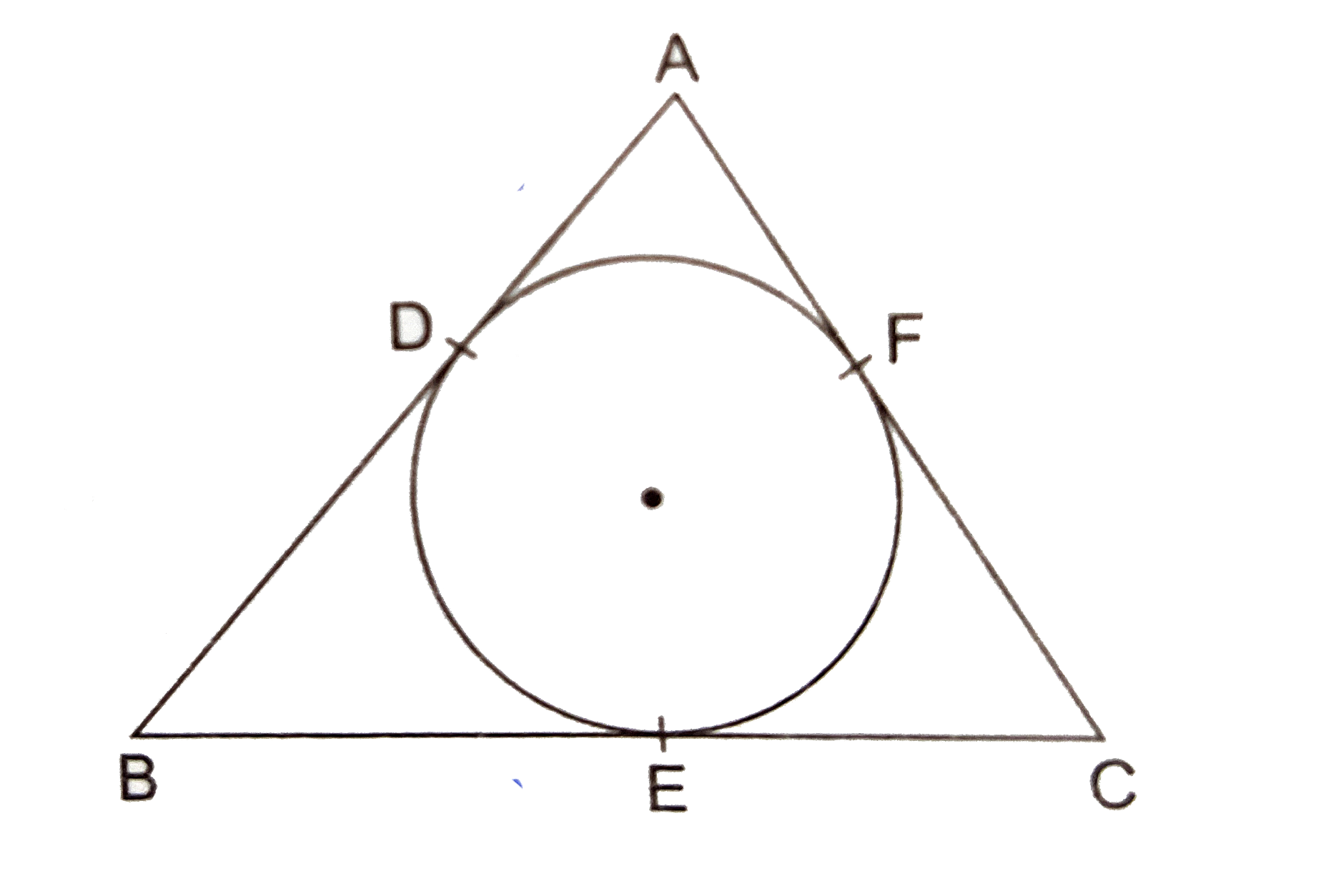
View SolutionIn the given figure, a circle inscribed in a triangle `ABC`, touches the sides `AB`, `BC` and `AC` at points `D`, `E` and `F` respectively. If `AB=12cm`, `BC=8cm` and `AC=10cm`, find the lengths of `AD`, `BE` and `CF`.
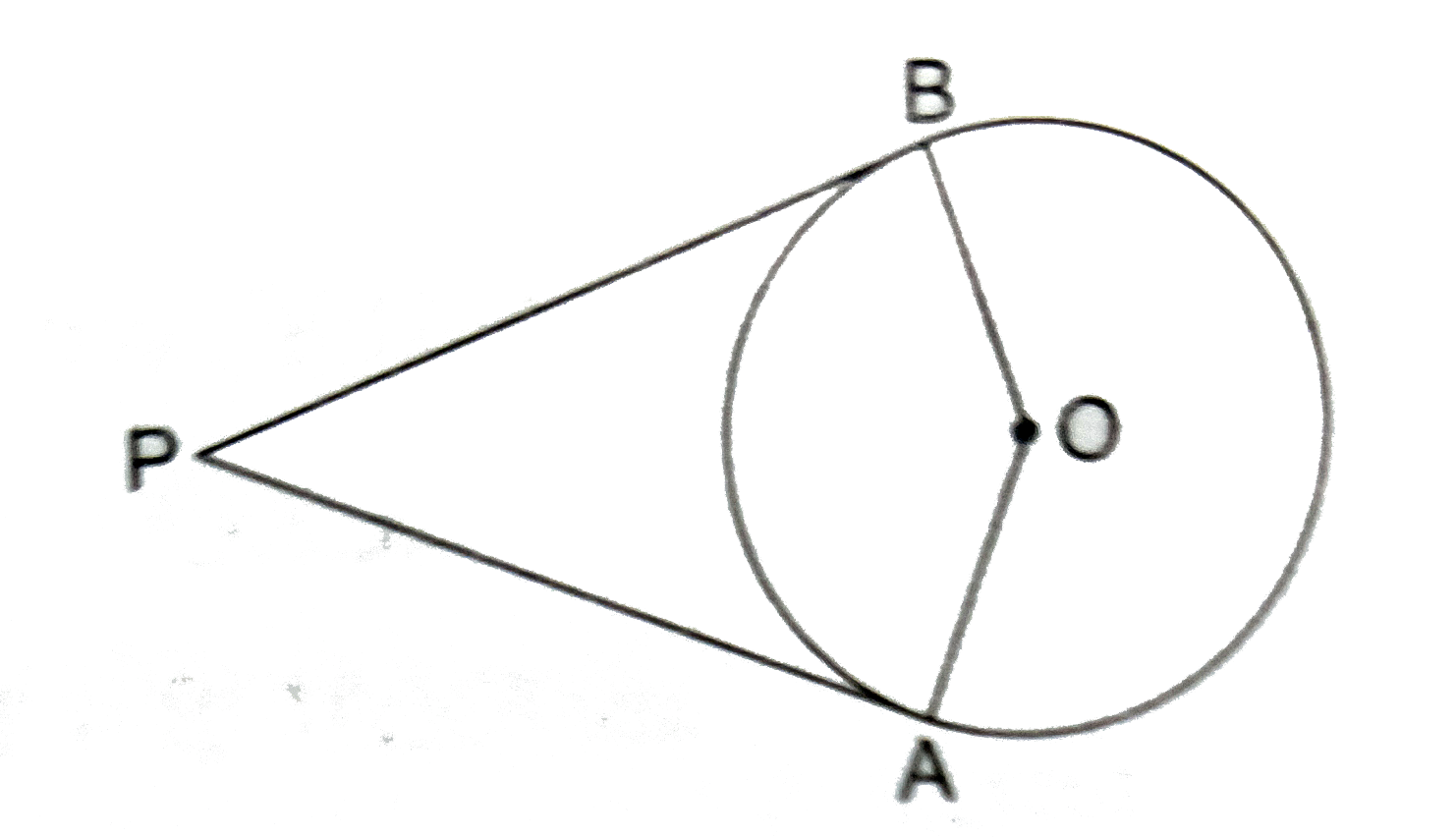
View SolutionIn the given figure, `PA` and `PB` are the tangent segments to a circle with centre `O`. Show that the points `A`, `O`, `B` and `P` are concyclic.
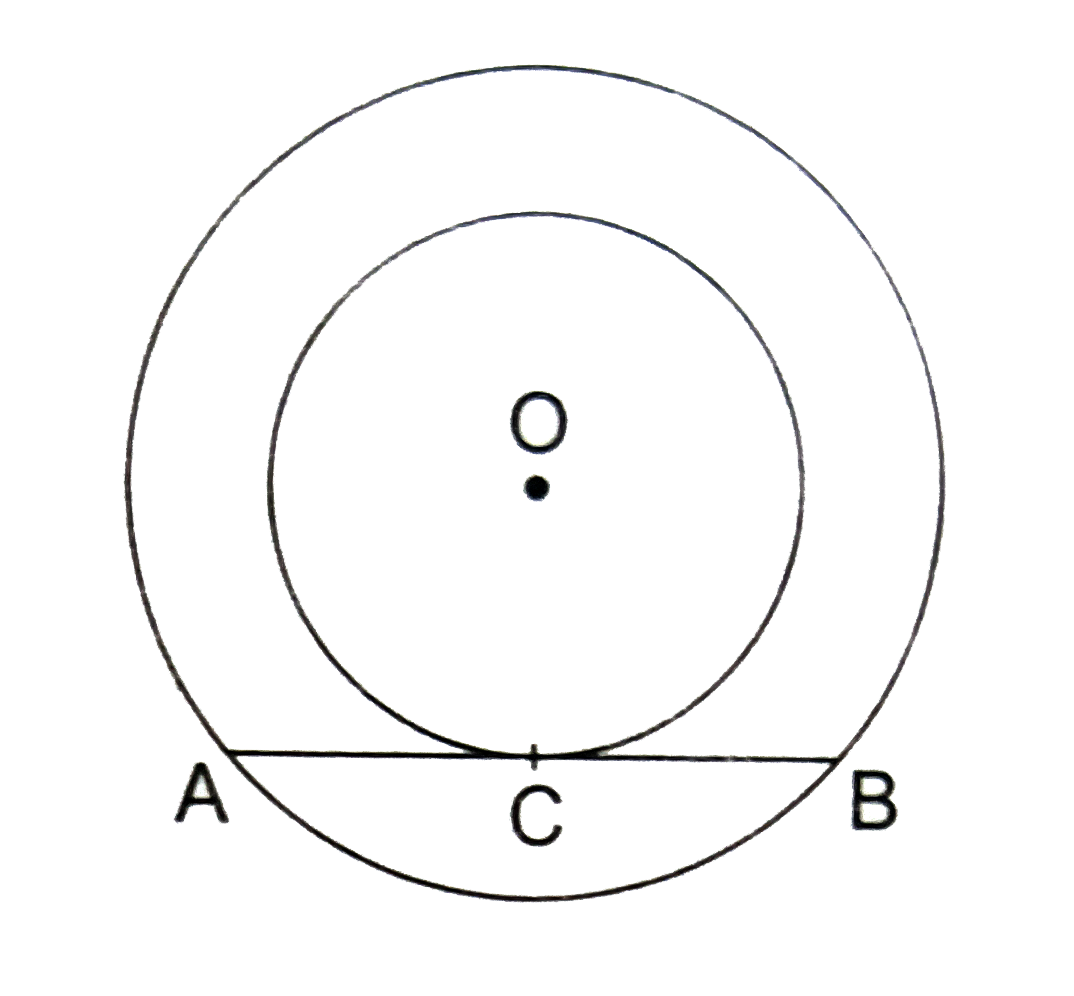
View SolutionIn the given figure, the chord `AB` of the larger of the two concentric circles, with centre `O`, touches the smaller circle at `C`. Prove that `AC=CB`.
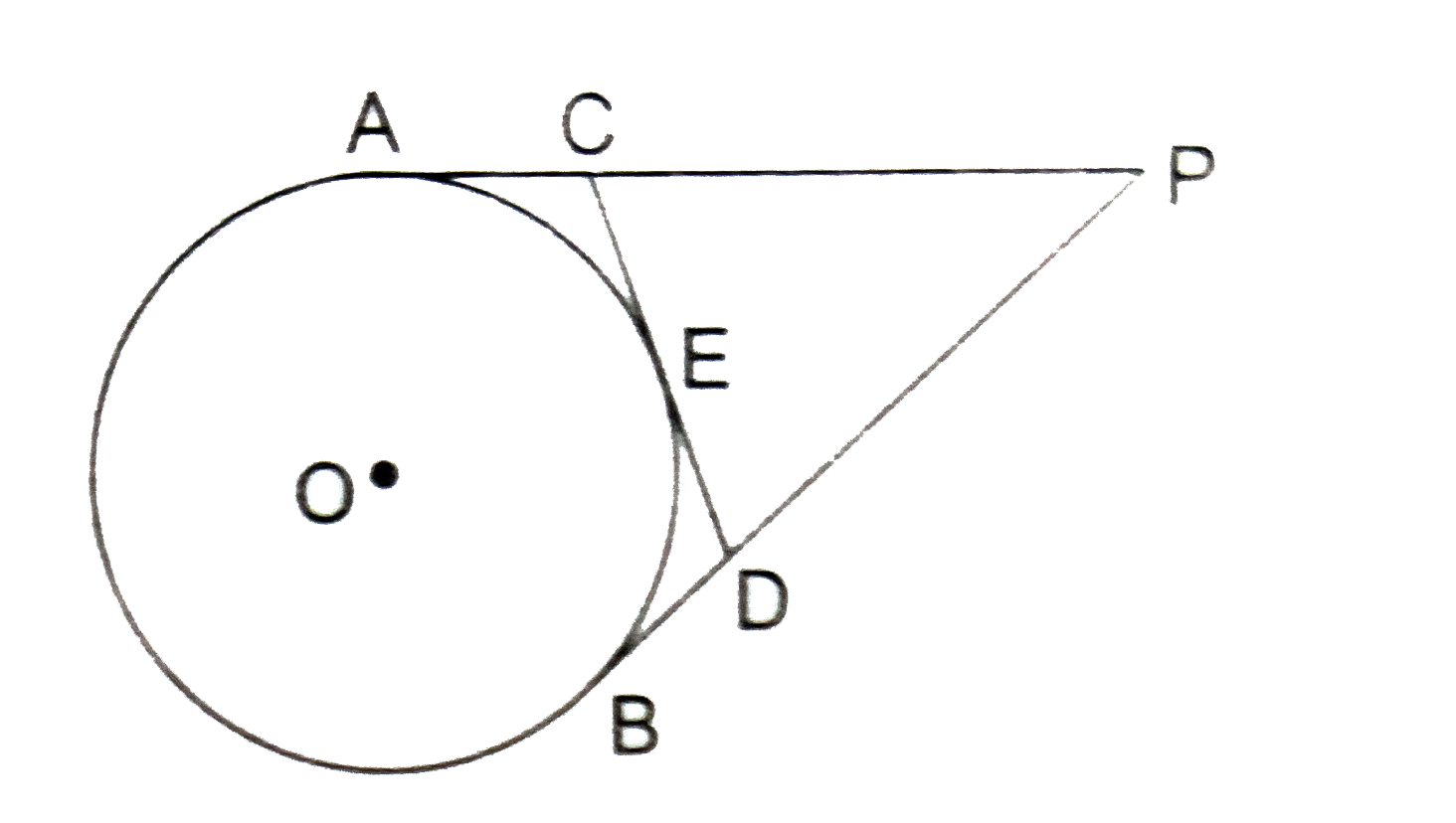
View SolutionFrom an external point `P`, tangents `PA` and `PB` are drawn to a circle with centre `O`. If `CD` is the tangent to the circle at a point `E` and `PA=14cm`, find the perimeter of `DeltaPCD`.
View SolutionA circle is inscribed in a `DeltaABC`, touching `AB`, `BC` and `AC` at `P`, `Q` and `R` respectively. If `AB=10cm`, `AR=7cm` and `CR=5cm`, find the length of `BC`.
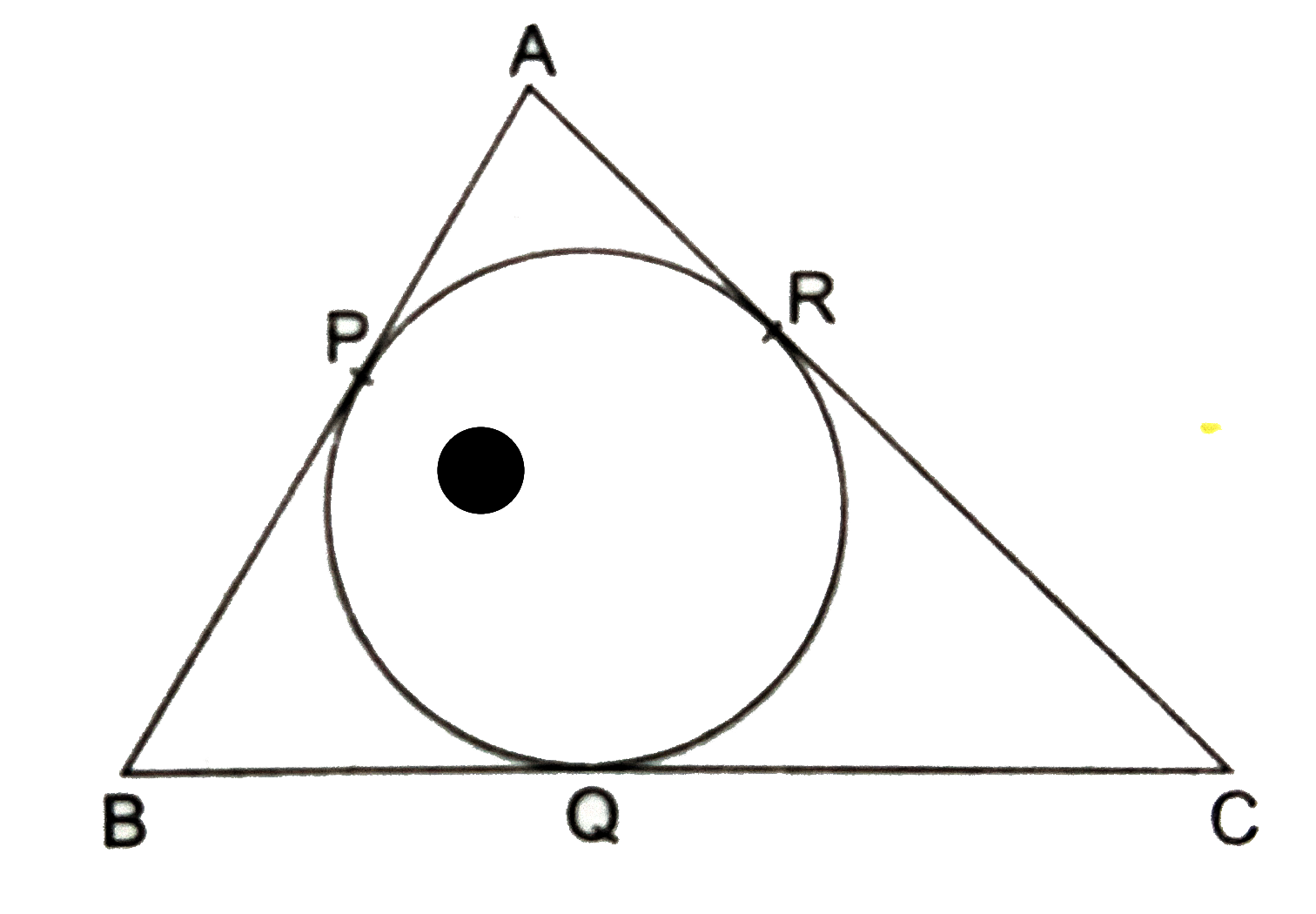
View SolutionIn the given figure, a circle touches all the four sides of a quadrilateral `ABCD` whose three sides are `AB=6cm`, `BC=7cm` and `CD=4cm`. Find `AD`.
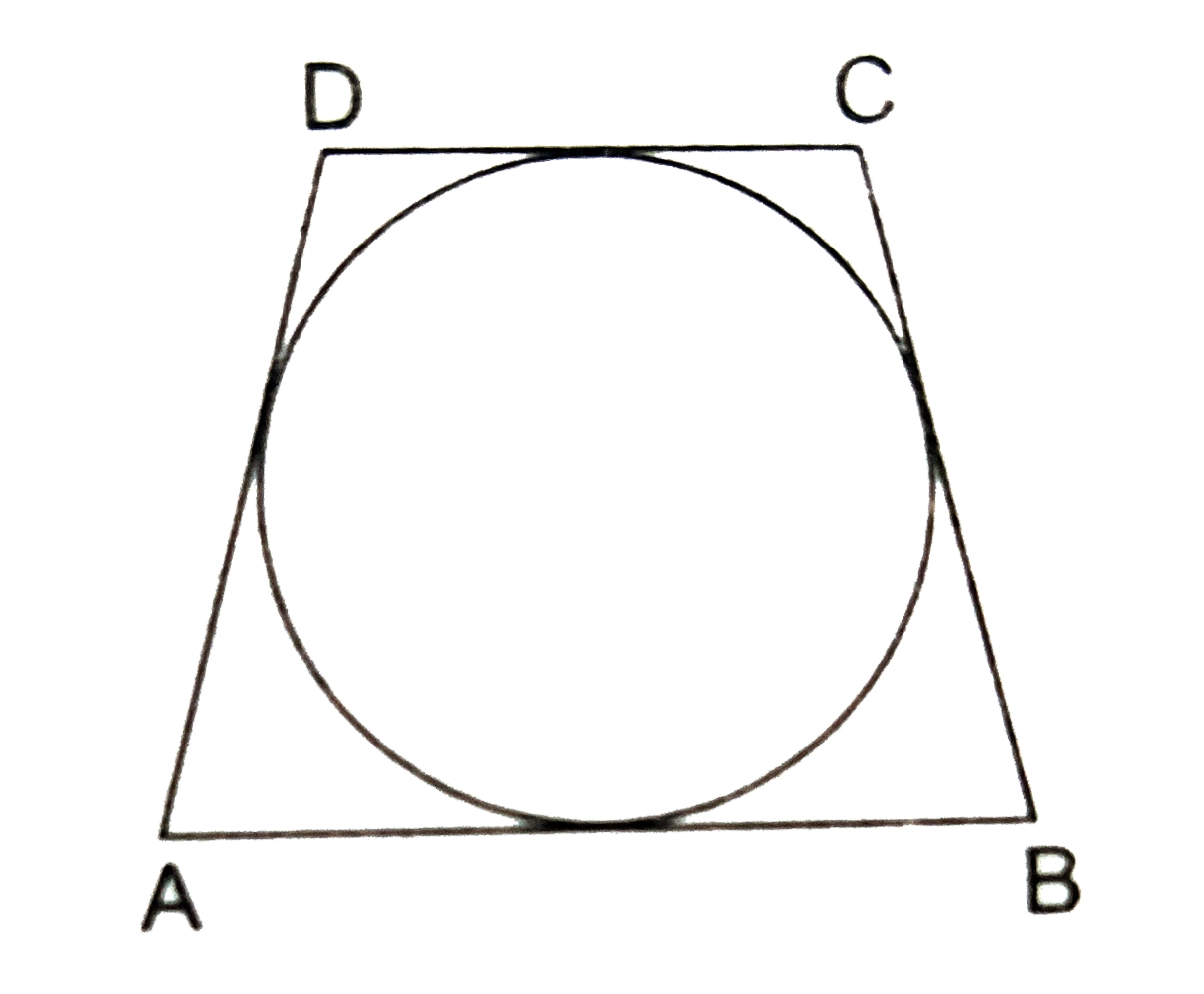
View SolutionIn the given figure, an isosceles triangle `ABC`, with `AB=AC`, circumscribes a circle. Prove that the point of contact `P` bisects the base `BC`.
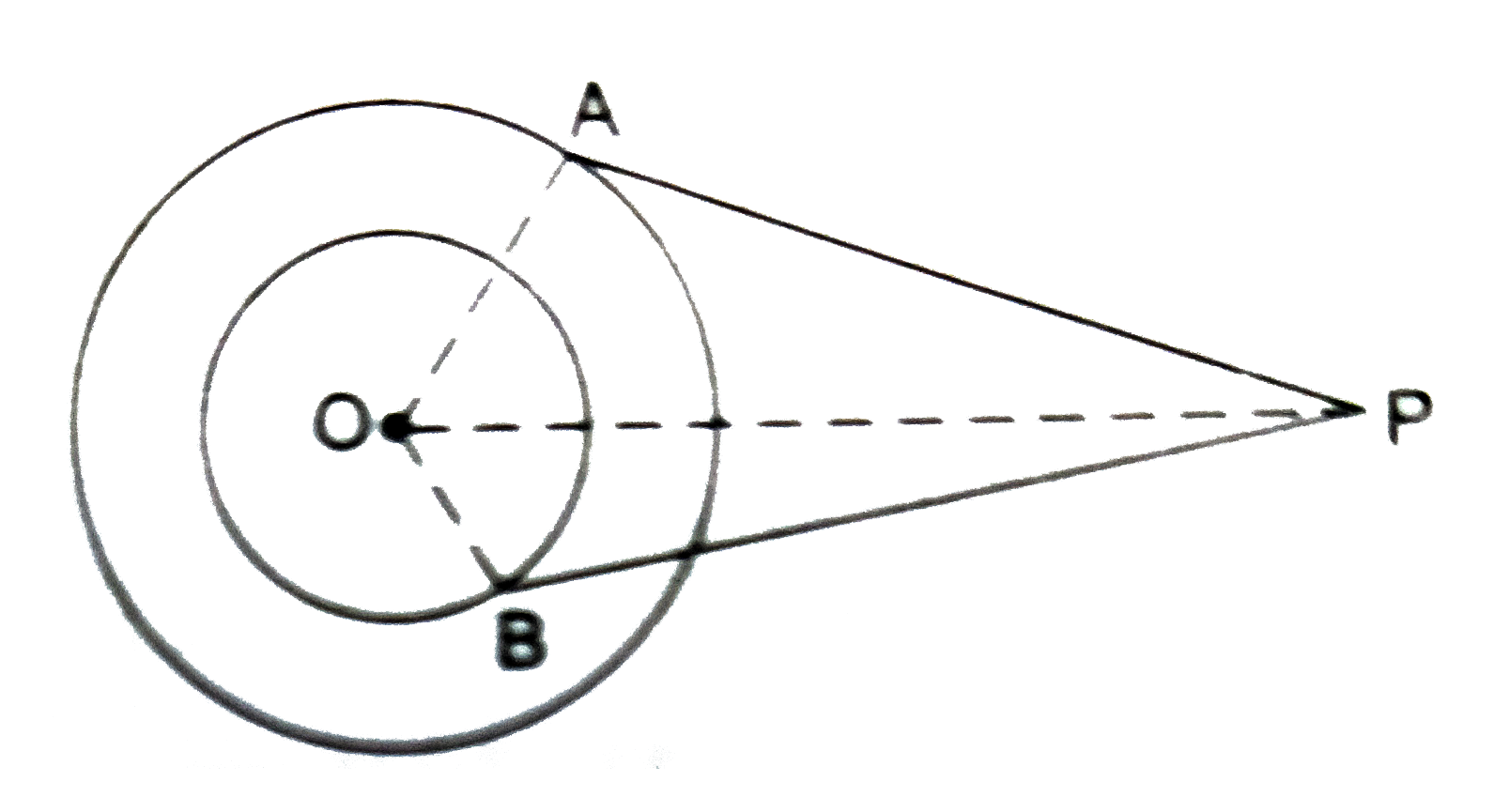
View SolutionIn the given figure, `O` is the centre of two concentric circles of radii `4cm` and `6cm` respectively. `PA` and `PB` are tangents to the outer and inner circle respectively. If `PA=10cm` , find the length of `PB` up to one place of decinal.
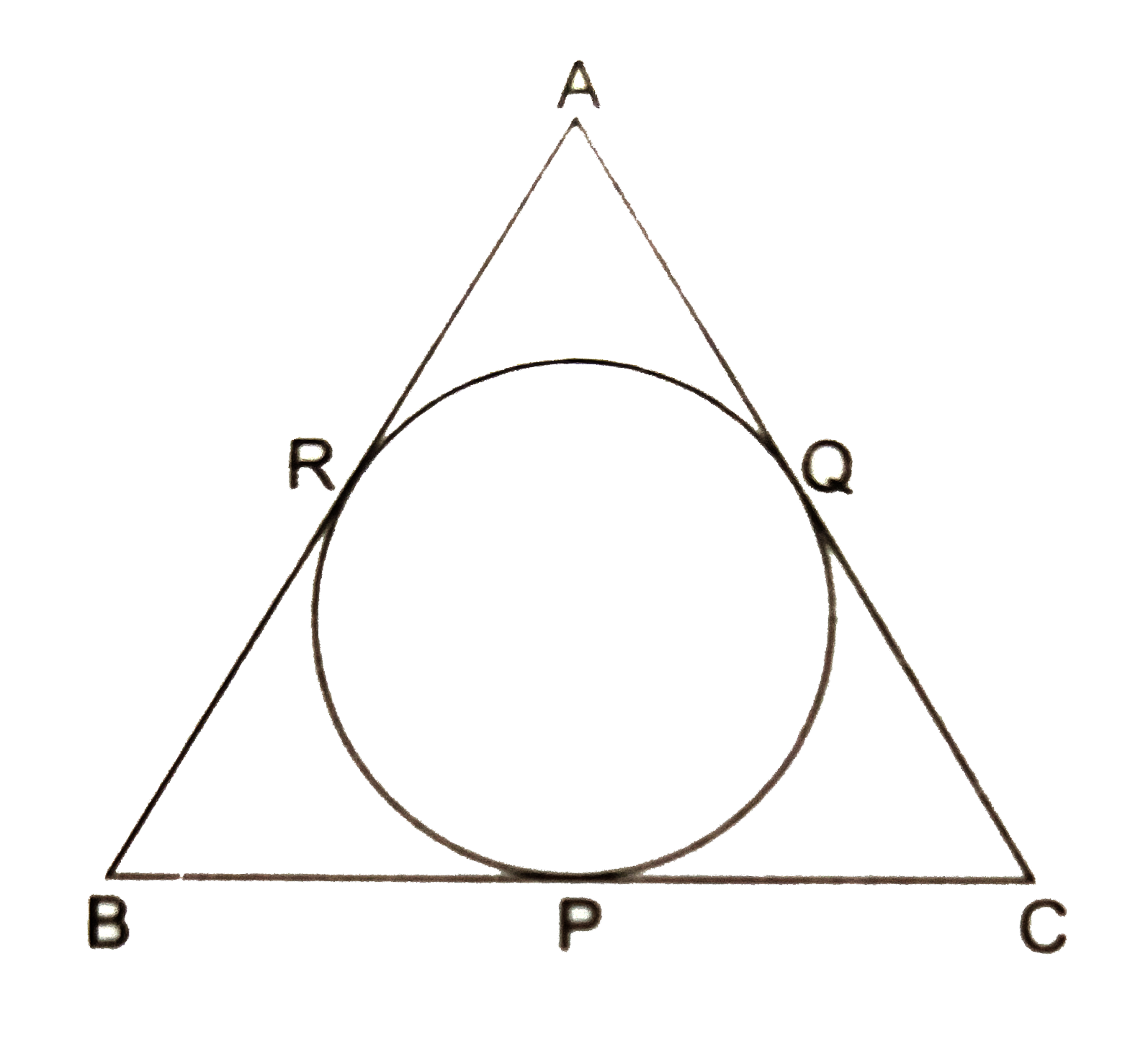
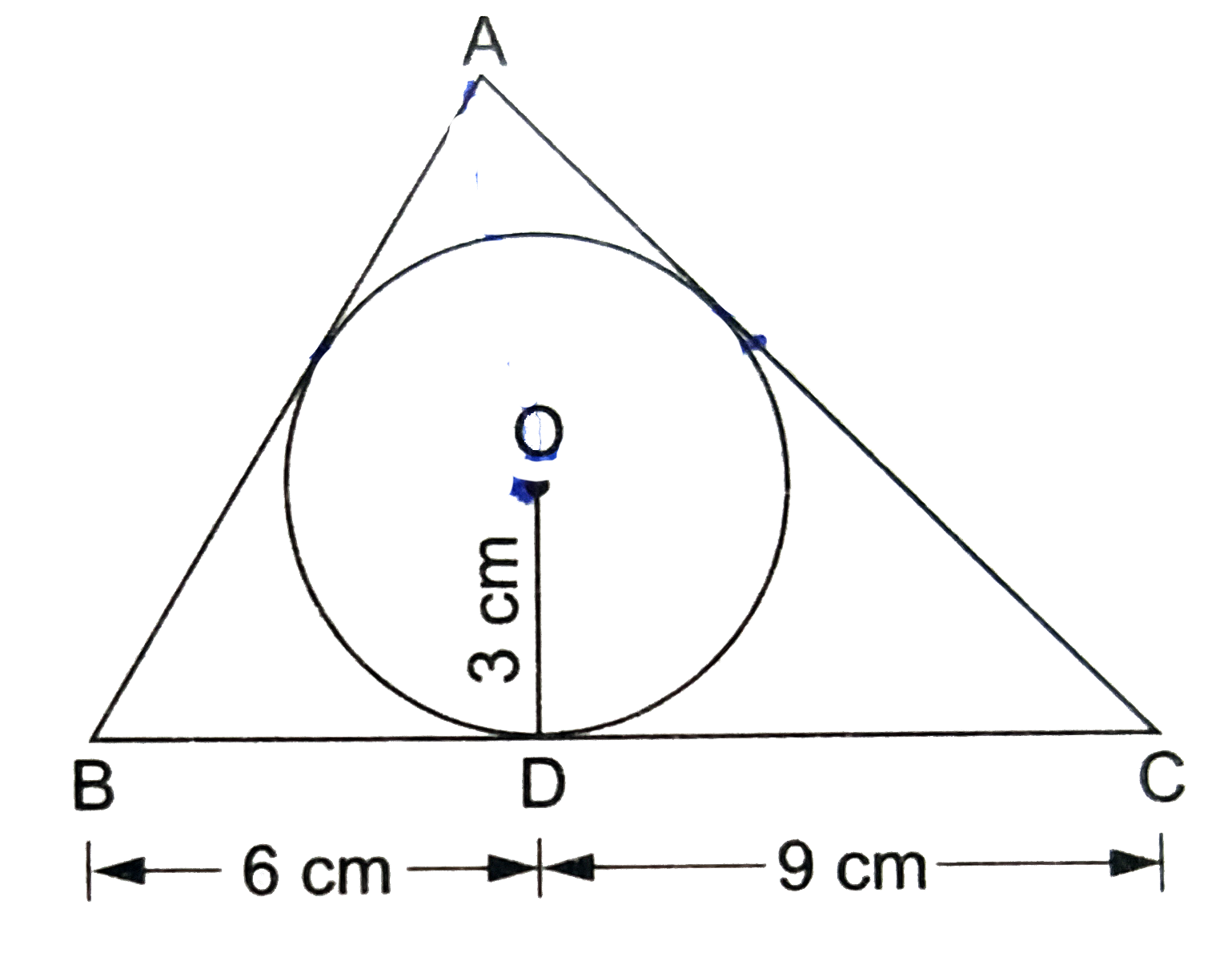
View SolutionIn the given figure, a triangle `ABC` is drawn to circuscribe a circle of radius `3cm`, such that the segments `BD` and `DC` into which `BC` is divided by the point of contact `D` are of lengths `6cm` and `9cm` respectively. If the area of `DeltaABC=54cm^(2)` then find the lengths of sides `AB` and `AC`.
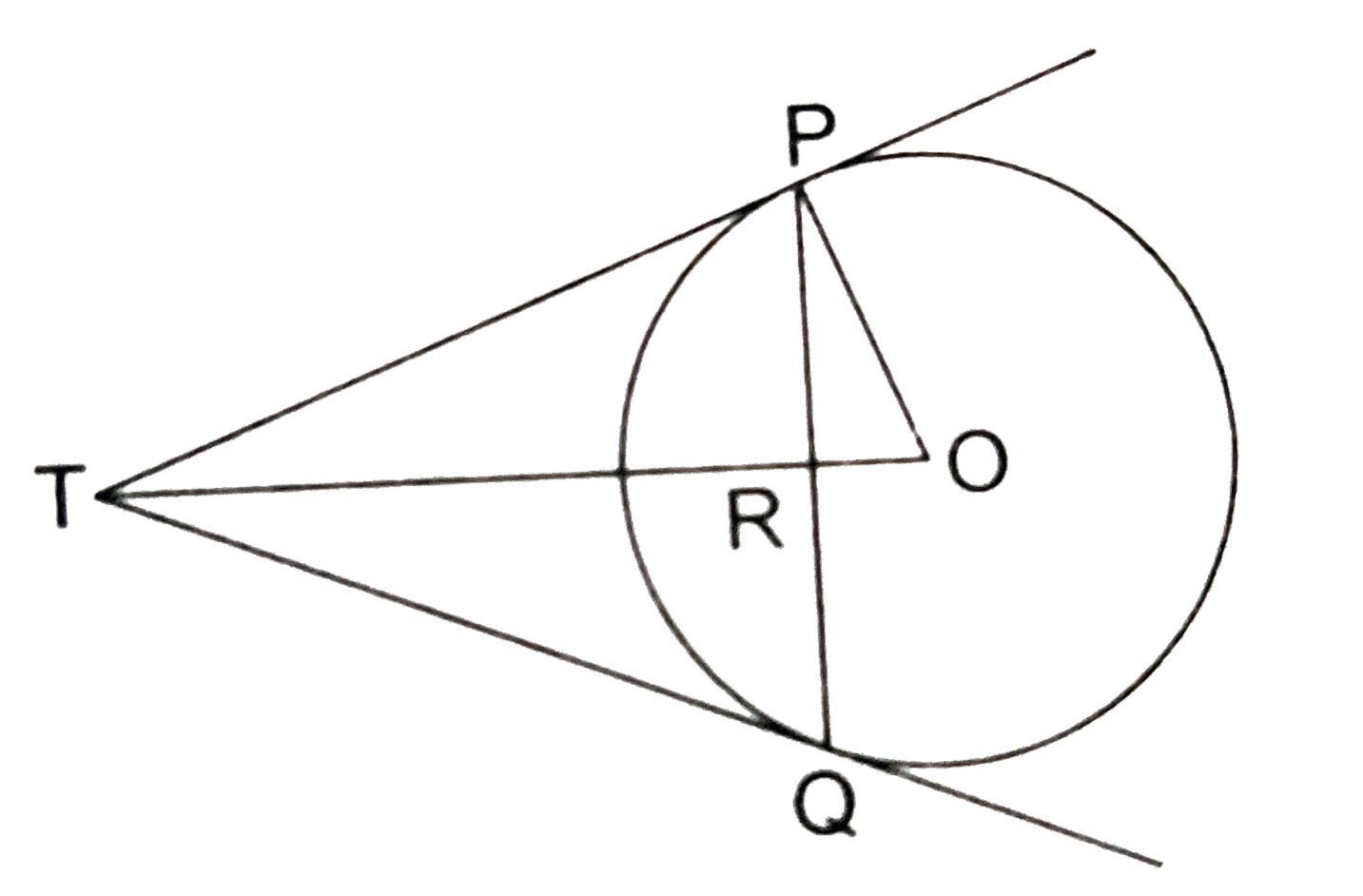
View Solution`PQ` is a chord of length `4.8cm` of a circle of radius `3cm`. The tangents at `P` and `Q` intersect at a point `T` as shown in the figure. Find the length of `TP`.
View SolutionProve that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
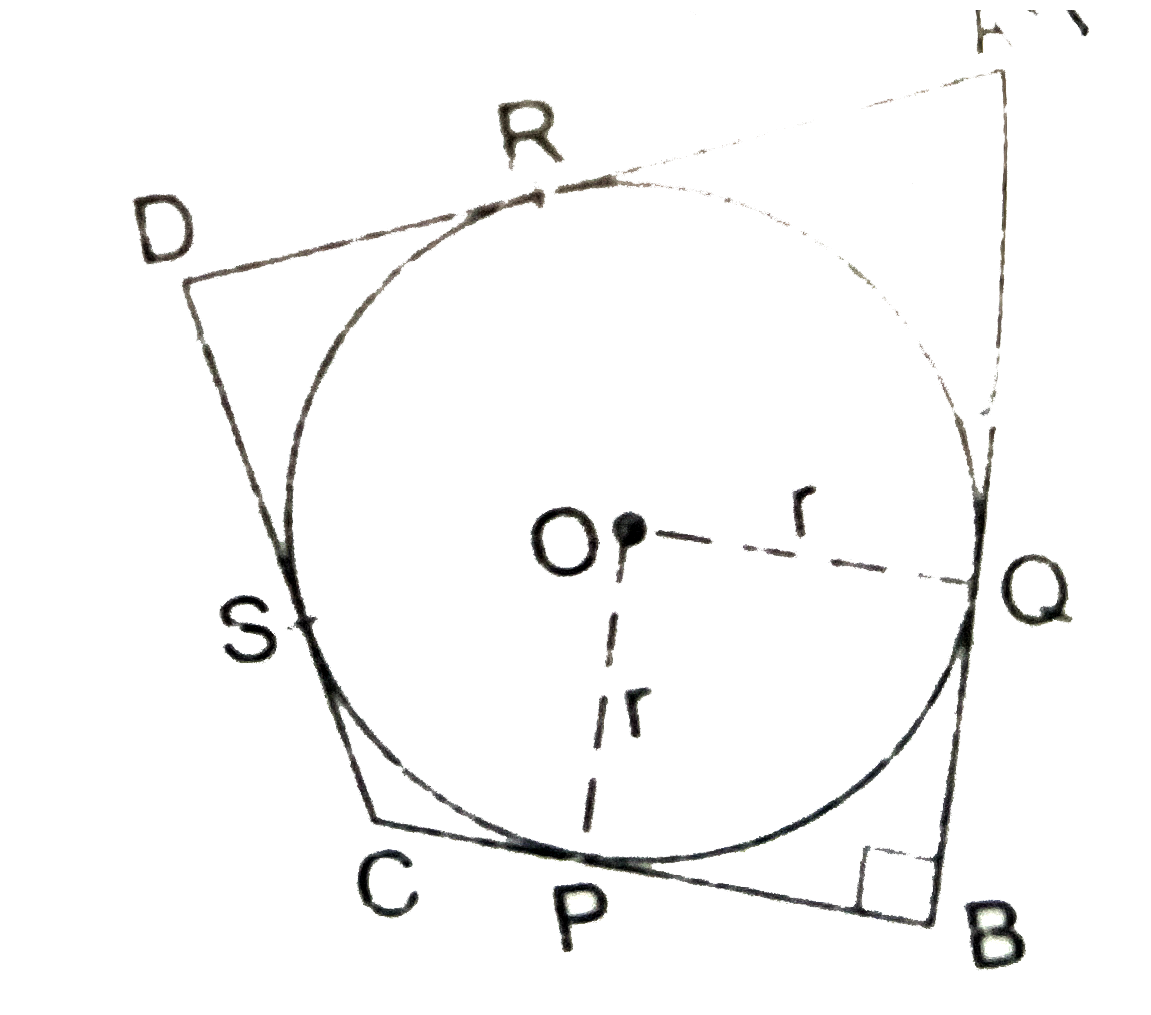
View SolutionIn the given figure, a circle with centre `O`, is inscribed in a quadrilateral `ABCD` such that it touches the side `BC`, `AB`, `AD` and `CD` at points `P`, `Q`, `R` and `S` respectively. If `AB=29cm`, `AD=23cm`, `/_B=90^(@)` and `DS=5cm` then find the radius of the circle.
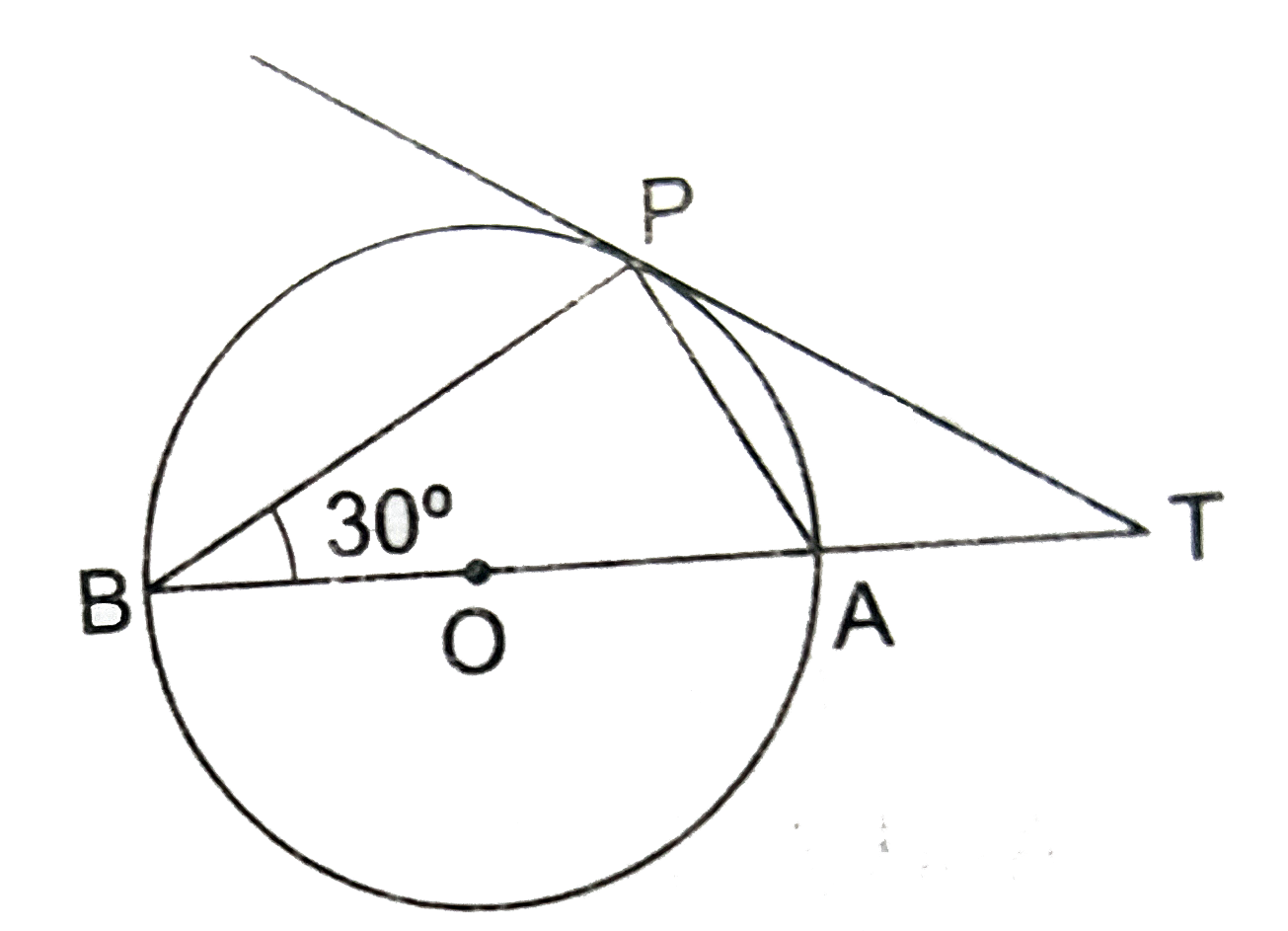
View SolutionIn the given figure, `O` is the centre of the circle and `TP` is the tangent to the circle from an external point `T`. If `/_PBT=30^(@)`, prove that `BA : AT =2 :1`.
View Solution
Exercise 8A questions and complete solutions for chapter CIRCLES of RS AGGARWAL MATHS (HINGLISH) of Class 10