Complete Solutions to Solved Examples of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
From a point `P`, `10cm` away from the centre of a circle, a tangent `PT` of length `8cm` is drawn. Find the radius of the circle.
View SolutionA tangent `PQ` at a point `P` of a circle of radius `5cm` meets a line through the centre `O` at a point `Q` so that `OQ=13cm`. Find the length of `PQ`.
View SolutionIn the given figure, `AB` is the diameter of a circle with centre `O` and `AT` is a tangent. If `/_AOQ=58^(@)`, find `/_ATQ`.
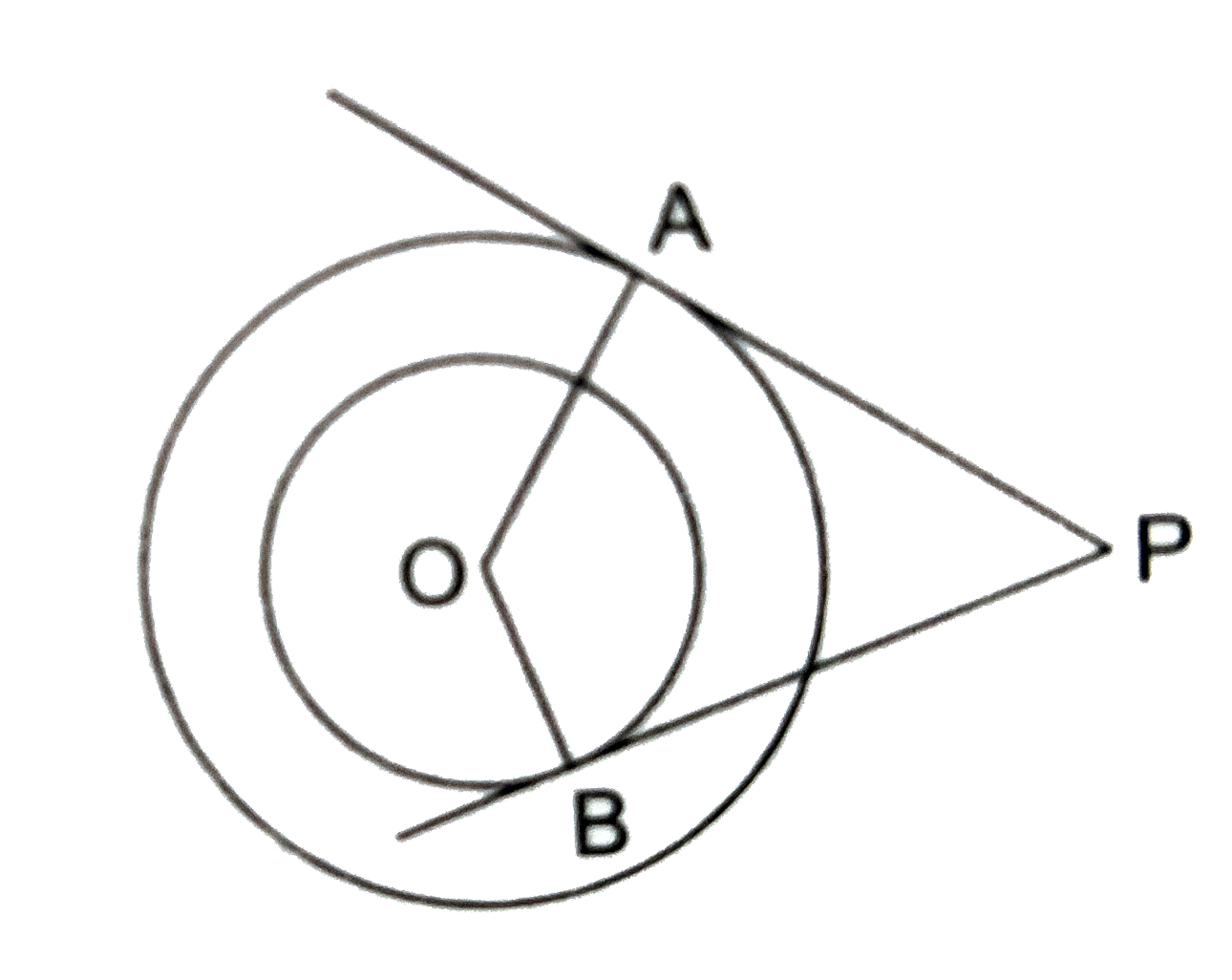
View SolutionTangents `PA` and `PB` are drawn from an external point `P` to two concentric circles with centre `O` and radii `8cm` and `5cm` respectively, as shown in the figure. If `AP=15cm` then find the length of `BP`.
View SolutionIn Fig. 10.21, two circles touch each other at the point `C` . Prove that the common tangent to the circles at `C` , bisects the common tangent at `P` and `Q` . (FIGURE)
View SolutionTwo concentric circles of radii `a` and `b(a gt b)` are given. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii `7cm` and `r cm` respectively, where `r gt 7`. A chord of the larger circle of length `46cm`, touches the smaller circle. Find the value of `r`.
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionFrom a point `P` outside a circle with centre `O`, tangents `PA` and `PB` are drawn to the circle. Prove that `OP` is the right bisector of the line segment `AB`.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionProve that tangent drawn at the mid point of the are of a circle is pallelar to the chord joing the ends of point of the are
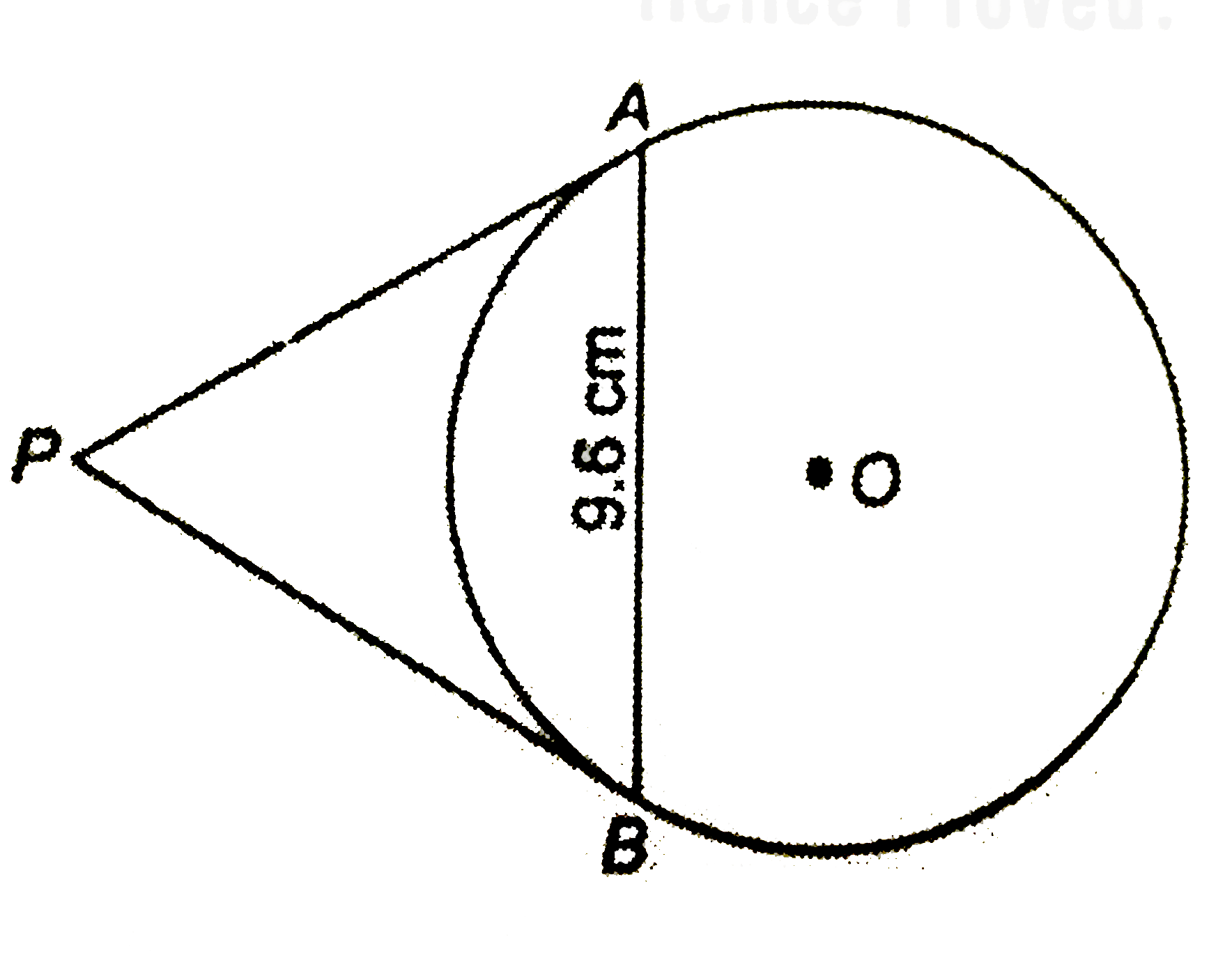
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
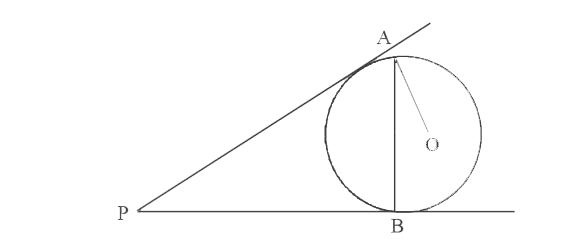
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that `angle APB = 2 angle OAB`
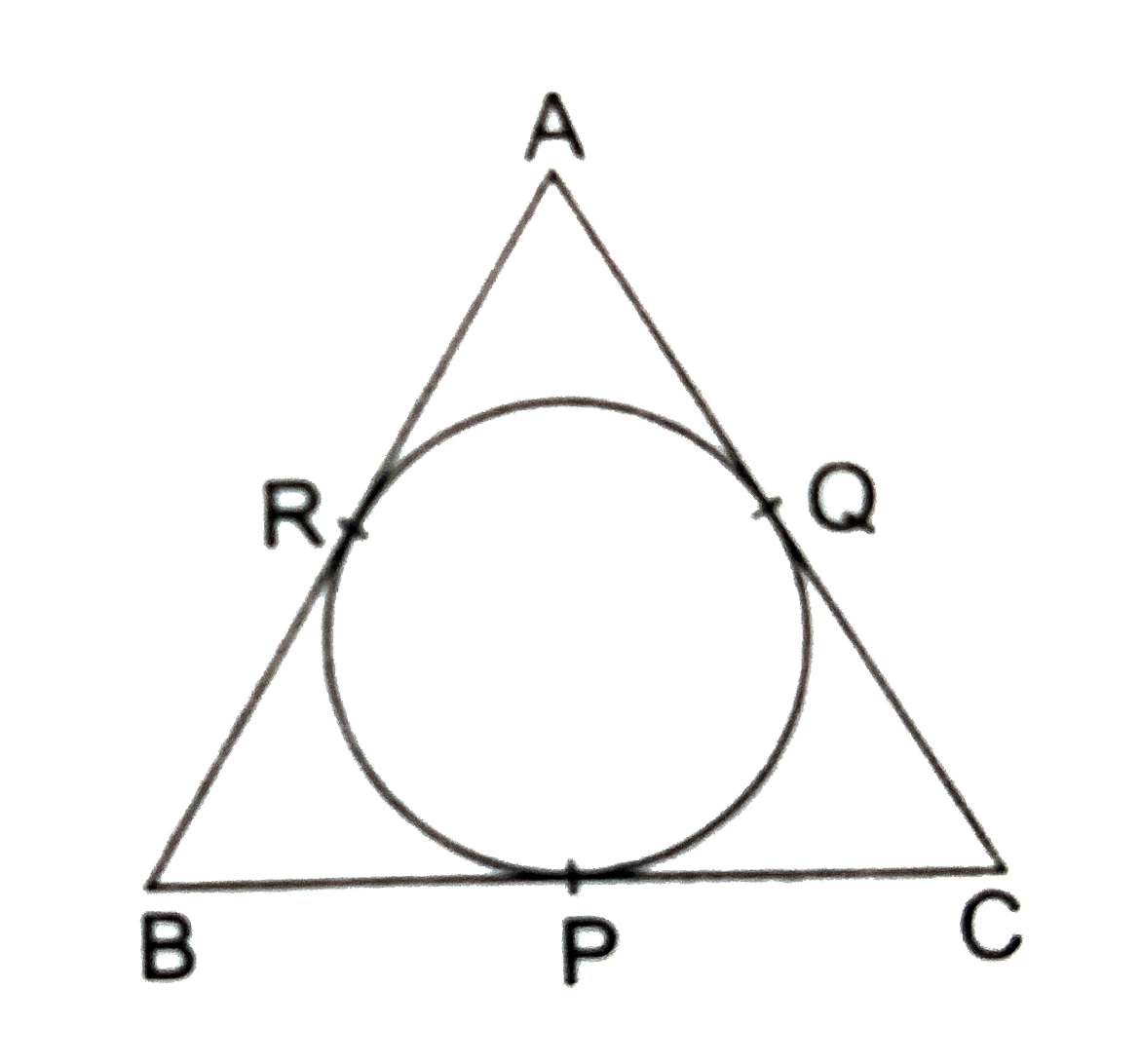
View SolutionIn the given figure, the incircle of `DeltaABC` touches the sides `BC`, `CA` and `AB` at `P`, `Q` and `R` respectively. Prove that
`(AR+BP+CQ)=(AQ+BR+CP)`
`=(1)/(2)("perimeter of"DeltaABC)`.
View SolutionIn fig , a circle isinscribed in a triangle PQR with PQ = 10 cm , QR = 8 cm and PR = 12 cm .Find the length of the QM , RN and PL.
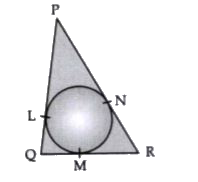
View SolutionA circle is inscribed in a `DeltaABC` touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR = 7 cm and CR = 5 cm, then find the length of BC.
View SolutionA circle is touching the side `BC` of `DeltaABC` at `P` and touching `AB` and `AC` produced at `Q` and `R` respectively. Prove that `AQ=(1)/(2)("perimeter of"DeltaABC)`.
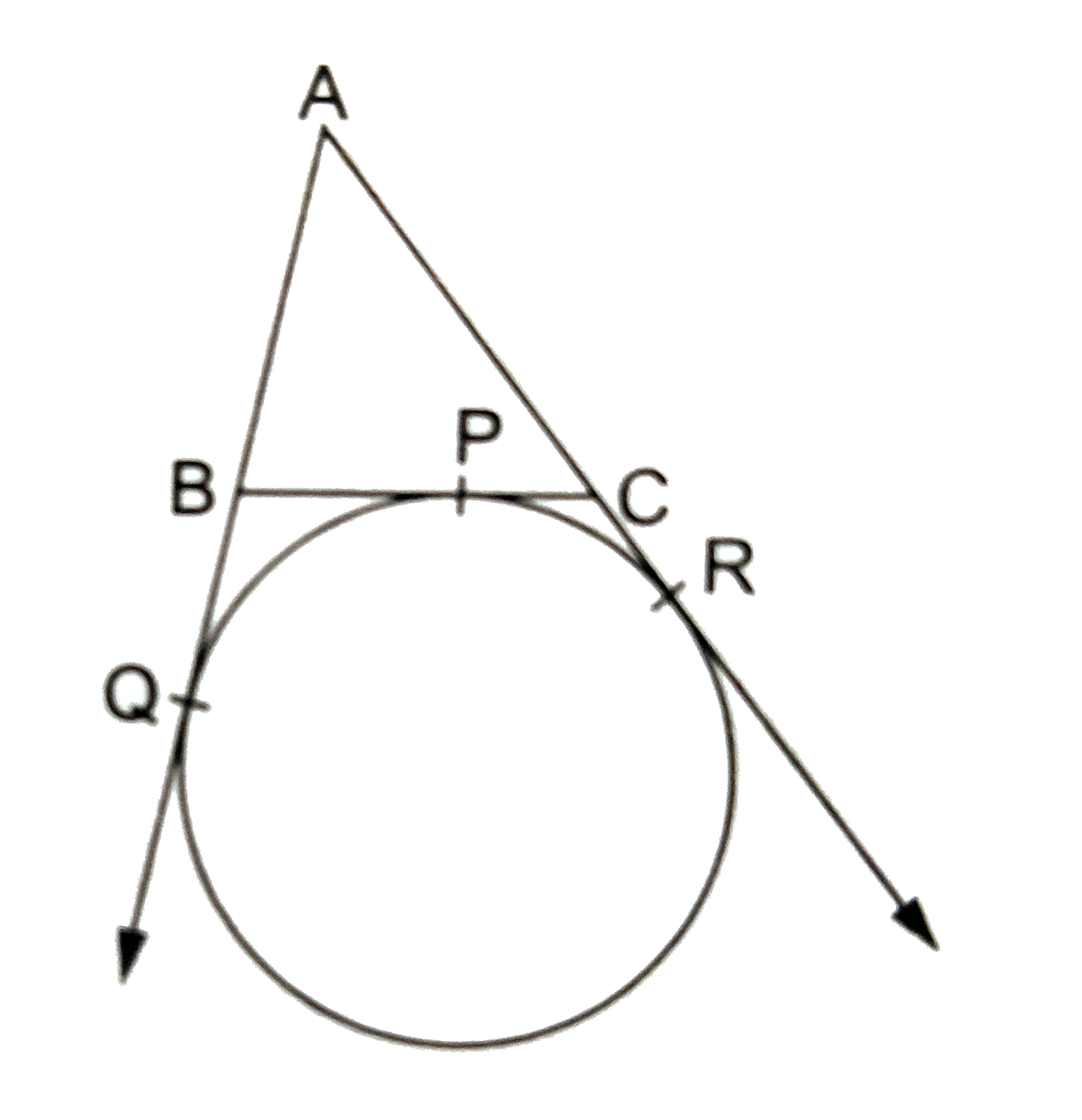
View Solution`PA` and `PB` are tangents to the circle with centre `O` from an external point `P`, touching the circle at `A` and `B` respectively. Show that the quadrilateral `AOBP` is cyclic.
View SolutionIn the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that `/_RPO = 30^@`. A chord RS is drawn parallel to the tangent PQ. Find `/_RQS`.
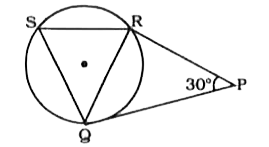
View SolutionIn the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : `(i) AB+CQ=AC+BQ`
(ii) Area `(triangleABC)=(1)/(2)("Perimeter of"triangleABC)xxr`
View SolutionIn the given figure, `ABC` is a right-angled triangle with `AB=6cm` and `AC=8cm`. A circle with centre `O` has been inscribed inside the triangle. Calculate the value of `r`, the radius of the inscribed circle.

View SolutionA triangle `ABC` is drawn to circumscribe a circle of radius `4cm` such that the segments `BD` and `DC` into which `BC` is divided by the point of contact `D` are of lengths `6cm` and `8cm` respectively. Find the lengths of the sides `AB` and `AC`.
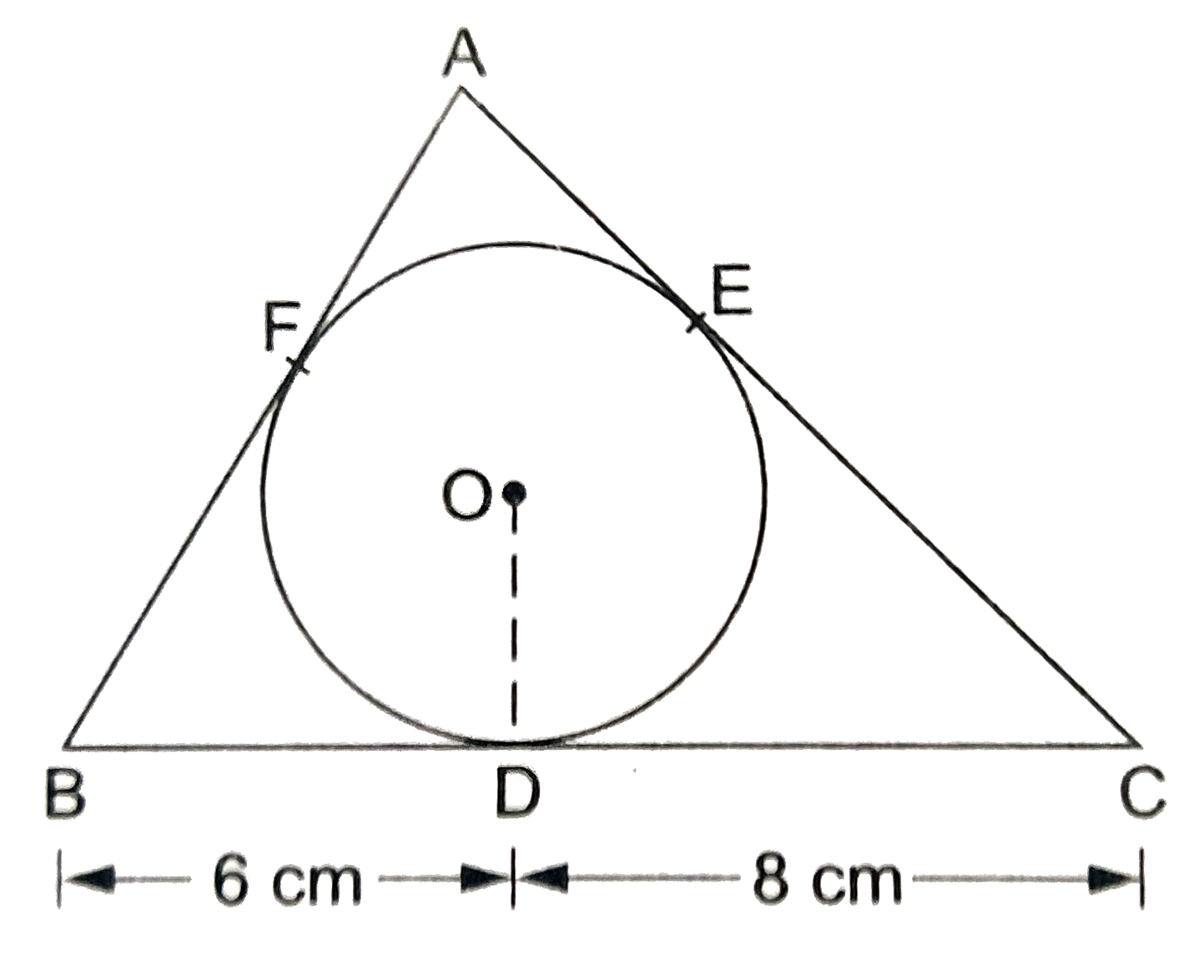
View SolutionIn the given figure, a triangle `ABC` is drawn to circuscribe a circle of radius `3cm`, such that the segments `BD` and `DC` into which `BC` is divided by the point of contact `D` are of lengths `6m` and `8cm` respectively. Find the side `AB`, if the area of `DeltaABC` is `63cm^(2)`.
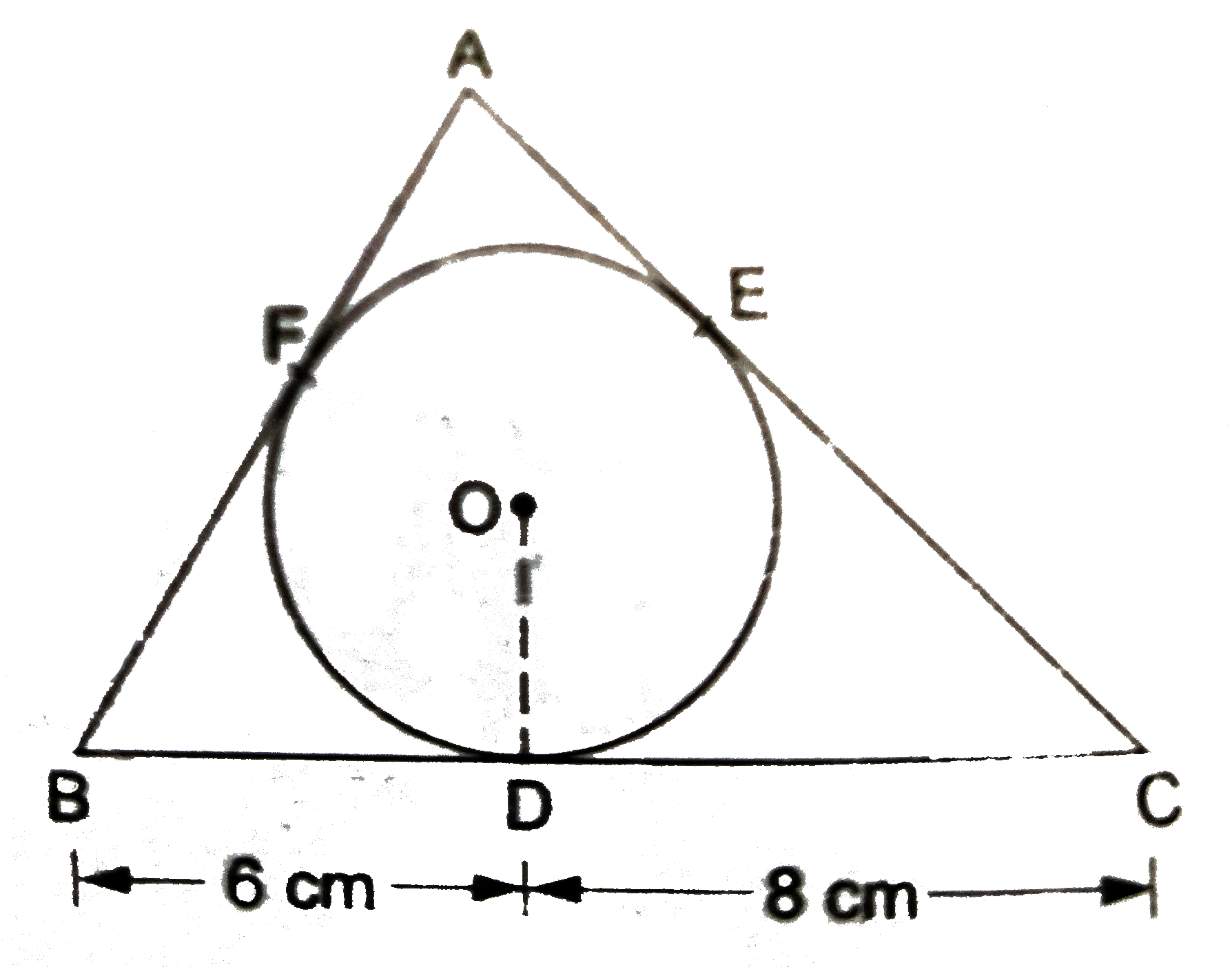
View SolutionIn the given figure, `XP` and `XQ` are two tangents to the circle with centre `O`, drawn from an external point `X`. `ARB` is another tangent, touching the circle at `R`. Prove that `XA+AR=XB+BR`.

View SolutionIf from an external point P of a circle with centre O, two tangents PQ and PR are drawn such `/_QPR=120^@`, prove that 2PQ=PO.
View SolutionA quadrilateral `ABCD` is drawn to circumscribe a circle, as shown in the figure. Prove that `AB+CD=AD+BC`.
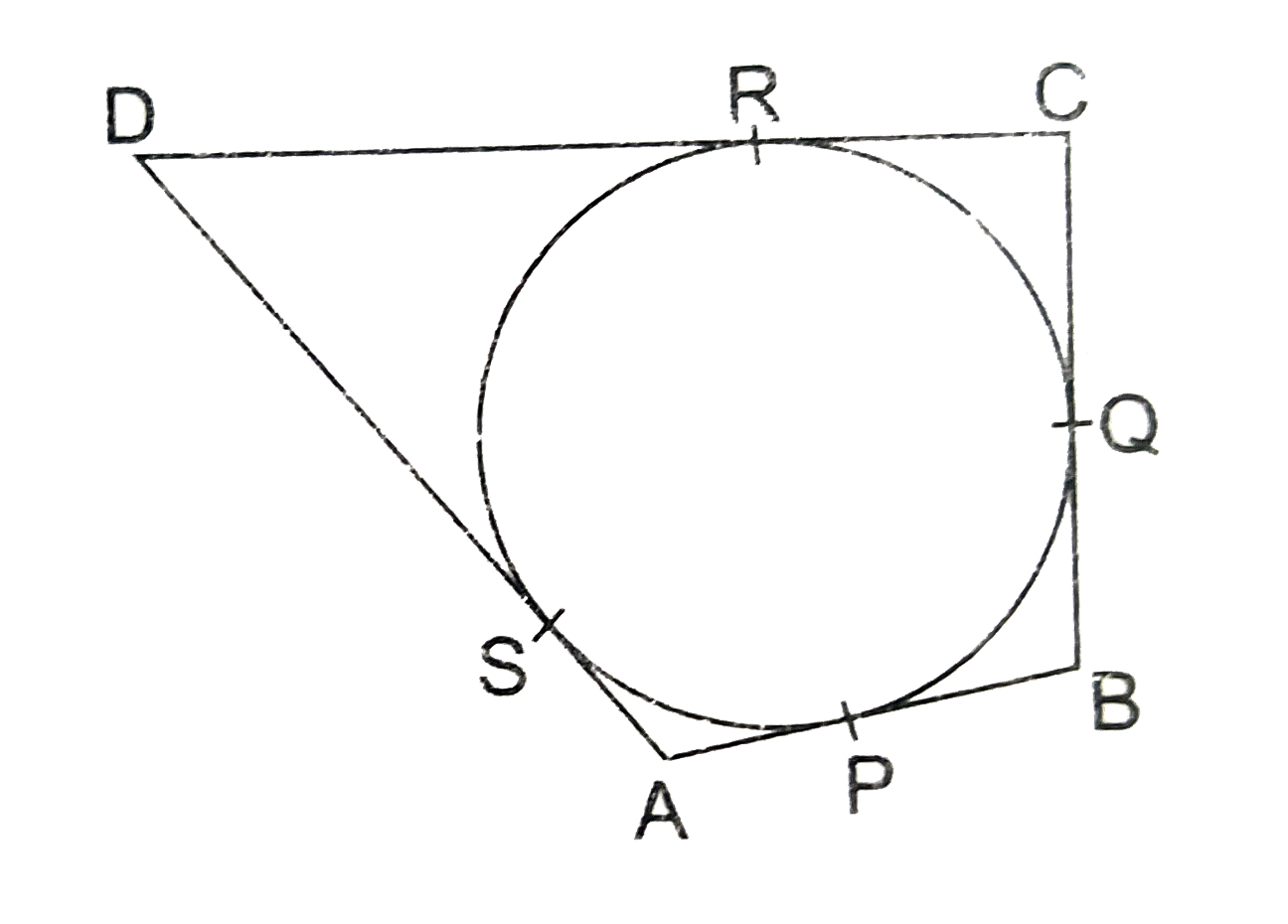
View SolutionIn the given figure, `ABCD` is a quadrilateral such that `/_D=90^(@)`. A circle with centre `O` and radius `r`, touches the sides `AB`, `BC`, `CD` and `DA` at `P`, `Q`, `R` and `S` respectively. If `BC=40cm`, `CD=25cm` and `BP=28cm`, find `r`.

View Solutionसिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है ।
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
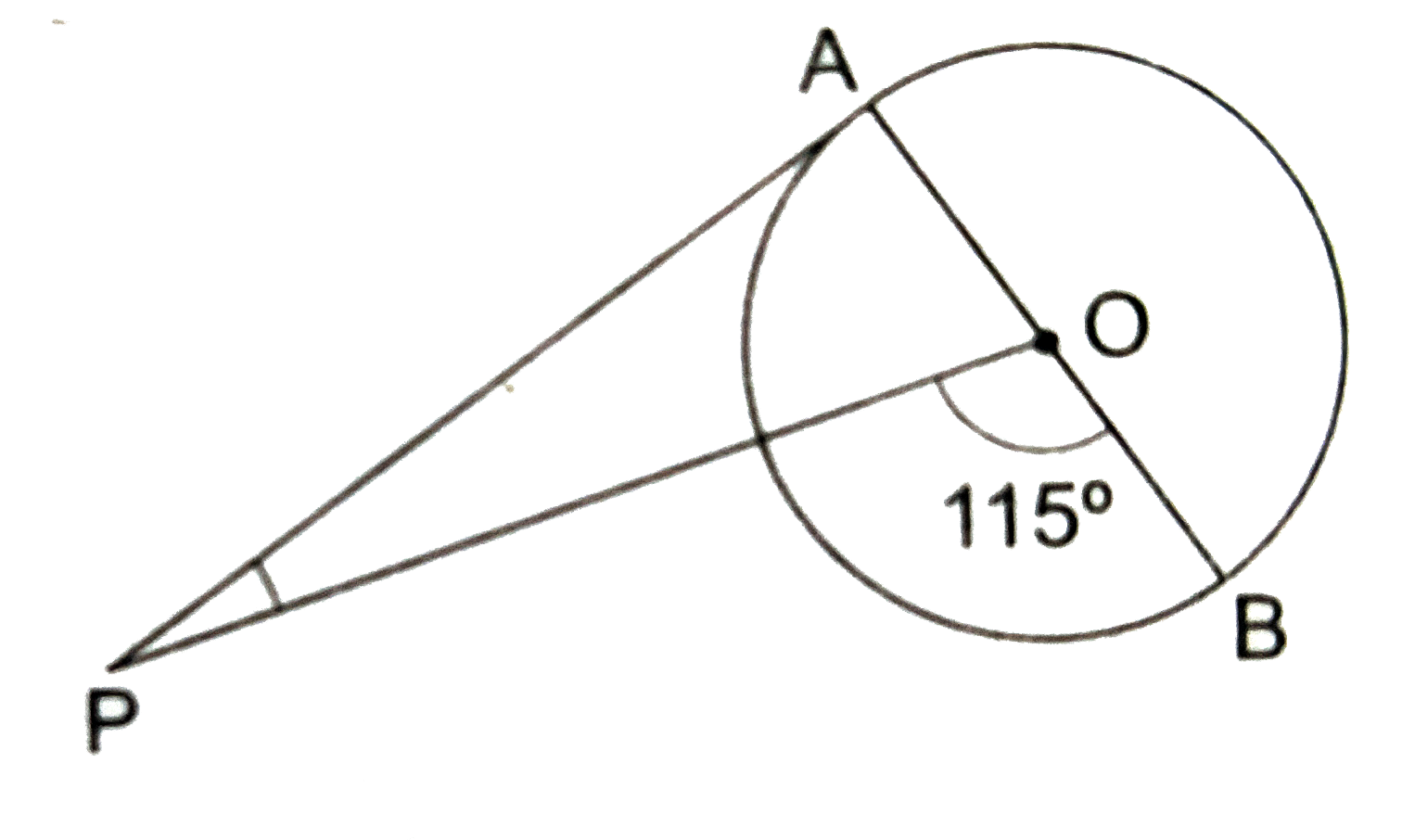
View SolutionIn the given figure, `PA` is a tangent from an external point `P` to a circle with centre `O`. If `/_POB=115^(@)`, find `/_APO`.
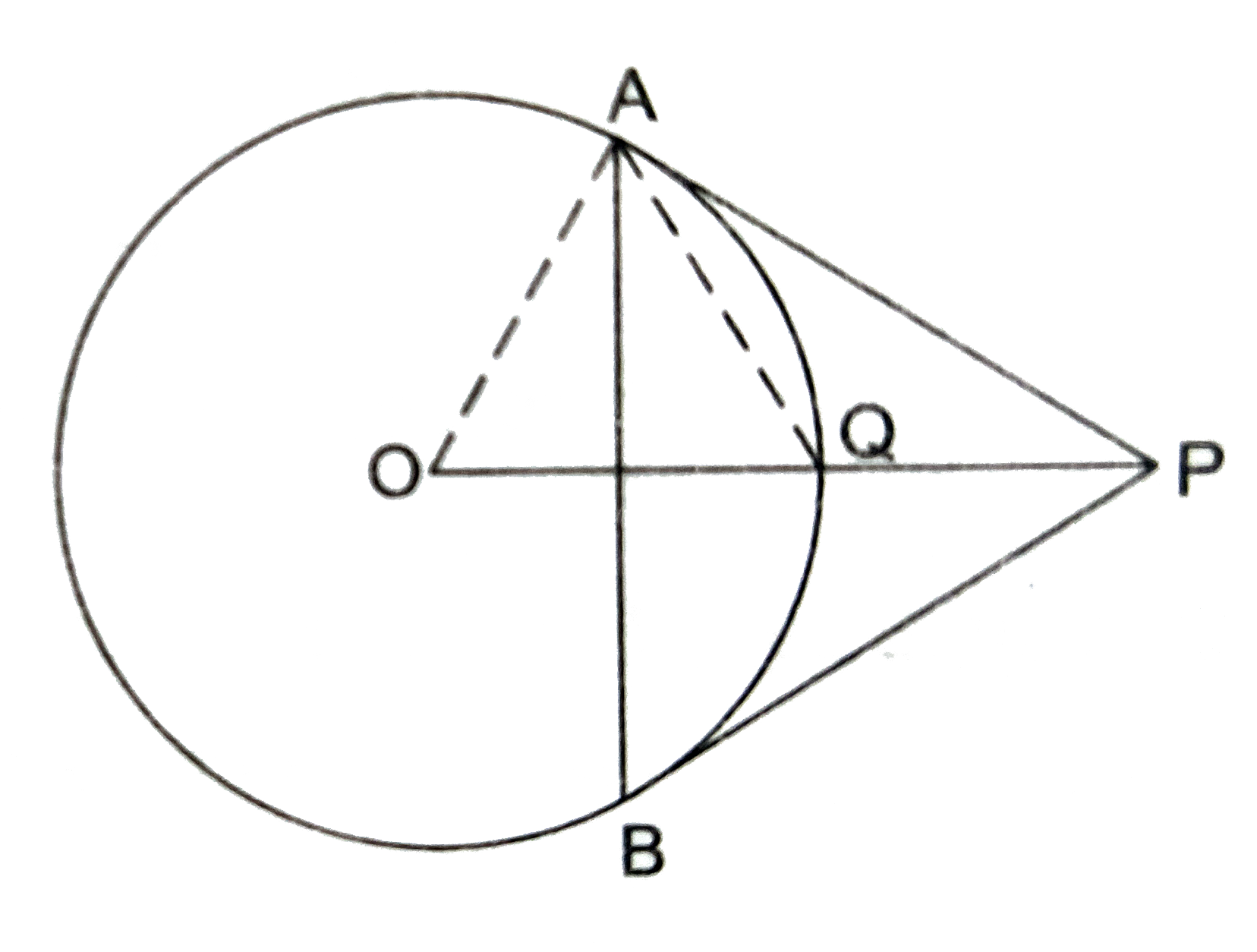
View SolutionFrom a point `P`, two tangents `PA` and `PB` are drawn to a circle `C(O,r)`. If `OP=2r`, show that `DeltaAPB` is equilateral.
View Solution`X Y`and `Xprime Yprime`are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting `X Y`at A and `XprimeYprime`at B. Prove that `/_A O B\ =\ 90^o`
View SolutionThe incircle of an isosceles triangle `ABC`, with `AB=AC`, touches the sides `AB`, `BC`, `CA` at `D,E` and `F` respectively. Prove that `E` bisects `BC`.
View Solution
Solved Examples questions and complete solutions for chapter CIRCLES of RS AGGARWAL MATHS (HINGLISH) of Class 10