Complete Solutions to MATHEMATICAL REASONING of chapter SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020 |
| SCIENCE OLYMPIAD FOUNDATION | MATHEMATICAL REASONING |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
If `x = (3+ sqrt7)/(2)` , then the value of `4x^2 + 1/x^2` is ______ .
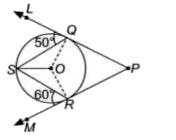
View SolutionIn the given figure, PQL and PRM are tangents to the circle with centre o at the points Q and R, respectively and S is a point on the circle such that `angleSQL = 50^@ and angleSRM = 60^@` . Then, `angleQSR` is equal to ______
View SolutionIn the given figure, `Delta`ABC is an equilateral triangle, the length of whose side is equal to 10 cm, and `Delta`DBC is right-angled at D and BD = 8 cm. Find the area of the shaded region. (Take `sqrt3` = 1.732)

View SolutionIf `2x^3+ax^2 + bx - 6 ` has (x-1) as a factor and leaves a remainder 2 when divided by (x-2) then the values of a and b respectively are _______ .
View SolutionFor what value of m, does the system of equations have a unique solution?
`x + 2y =3 `
`5x+ my = 3 `
View SolutionFind the coordinates of the centroid of a triangle whose vertices are `(0,\ 6),\ (8,\ 12)` and `(8,\ 0)` .
View SolutionFind the mode for the following data.

View SolutionWater is flowing at the rate of 15 km per hour though a pipe of diameter 14 cm into a rectangular which is 50 m long and 44 m wide. Find the time in which the level of water in the tank will rise by 21 cm.
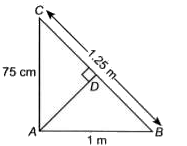
View SolutionIn the given figure, `angle`CAB = `90^@` and AD `bot` BC. Find AD.
View SolutionIf `sin theta+cos theta=p` and `sec theta + cosec theta=q`, find `q(p^2-1)=`
View SolutionA box contains 12 green balls and some red balls. If the probability of drawing a red ball from the box is twice that of drawing a green ball, then find the number of red balls in the box.
View SolutionIf the first second and last terms of an A.P. are a, b and 2a respectively, then its sum is
View SolutionA chord of a circle subtends an angle of `60^@` at the centre. If the length of the chord is 100 cm, then find the area of the major segment.
View SolutionIn `DeltaABC`, side AB is produced to D so that BD = BC . If `angleB =60^@` and `angleA =70^@` , then
View SolutionIf `x=acos^(3)theta,y=bsin^(3)theta` then `((x)/(a))^((2)/(3))+((y)/(b))^((2)/(3))=?`
View SolutionFrom a window 60 m high above the ground of a house in a street, the angle of elevation and depression of the top and the foot of another house on the opposite side of the street are `60^(@)` and `45^(@)` respectively. Show that the height of opposite house is `60(1+sqrt(3))` metres.
View SolutionThe roots of the equation `x^(2/3)+x^(1/3)-2=0` are
View SolutionIn figure, AB || EF, `angleABC` = 70° and `angle`EFD =`40^@`, find the value of x.

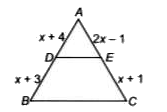
View SolutionIn the given figure, DE || BC. Find the value of x.
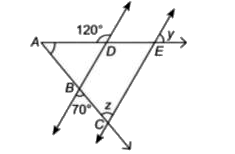
View SolutionIn the figure BD || CE, find the value of y and z respectively.
View Solution
MATHEMATICAL REASONING questions and complete solutions for chapter SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020 of HT Olympiad Previous Year Paper of Class 10