Complete Solutions to EXERCISE of chapter ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) |
| SUBHASH PUBLICATION | EXERCISE |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
Write the formula to find the sum of first n terms of an Arithmetic progression, whose first term is a and the last term is `a_n`.
View SolutionIf a pair of linear equations represented by lines has no solutions (inconsistent) then write what kinds of lines are these.
View SolutionWrite the formula to find area of a sector of a circle, if angle at the centre is `'theta'` degrees.
View SolutionWrite 96 as the product of prime factors.
View SolutionFind the degree of the polynomial
`P(x)=x^3+2x^2-5x-6`
View SolutionIna `Delta ABC, angle ABC=90^@ and angle ACB=30^@` then find `AB:AC`.
View SolutionFind the solution for the pair of linear equations:
`x+y=14`
`x-y=4`
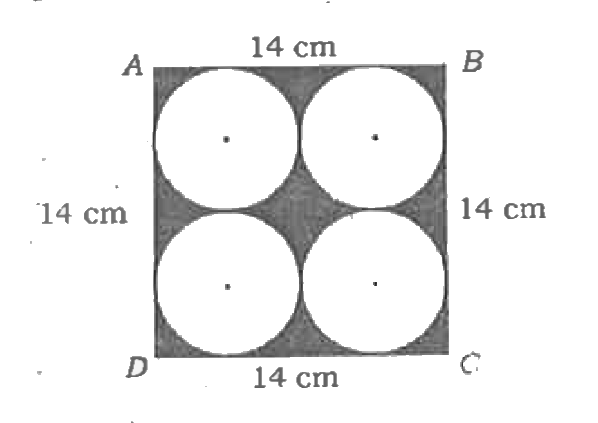
View SolutionABCD is a square of side 14cm. Four congruent circles are drawn in the square as shown in figure. Calculate the area of the shaded region.
[ Circles touch each other externally and also sides of the square]
View SolutionFind the distance between the points `(2,3) and (4,1)`.
View SolutionFind the area of a triangle whose vertices are `(1,-1),(-4,6) and (-3,-5)`.
View SolutionProve that `5+sqrt3` is an irrational number.
View Solution`Delta ABC~Delta DEF` and their areas are `64 cm^2 and 100 cm^2` respectively. If `EF=12 cm` then find the measure of BC.
View SolutionA verticle pole of height 6m casts a shadow 4m long on the ground, and at the same time a tower on the same ground casts a shadow 28m long. Find the height of the tower.
View SolutionThe diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that `DFxxEF=FB=FA`.
View Solutionsum and product of the zeroes of a quadratic polynomial `P(x)=ax^2+bx-4 "are" 1/4 and -1` respectively. Then find the values of a and b.
View SolutionFind the quotient and remainder when `p(x)=2x^2+2x+1` is divided by `g(x)=x+2`
View SolutionFind the value of k, in which one of its zeros is `-4` of the polynomial `P(x)=x^2-x-(2k+2)`.
View SolutionSolve the equation `x^2-3x-10=0` by using formula.
View SolutionIf `cosec theta=(13)/(12)` then find the value of `cos theta`.
View Solution`tan A . Sin A+ cos A=secA`
View SolutionA box contains 90 discs. Which are numbered from 1 to 90. If one disc is drawn at randow from the box. Find the probability that is bears a perfect square number.
View SolutionA metallic sphere of radius 9cm is melted and recast into the shape of a cyclinder of radius 6 cm. Find the height of the cyclinder.
View SolutionThe faces of two cubes of volume `64 cm^3` each are joined together to form a cuboid. Find the total surface area fo the cuboid.
View SolutionProve that the "Length of tangents drawn from an external point a circle are equal".
View SolutionTwo concentric circle of radii 5 cm and 3cm are drawn. Find the length of the chord of the larger circle which touches the smaller circles.
View SolutionFind the mode for the following data in the frequency distribution table:
View SolutionFind the median for the following data in the frequency distribution table:

View SolutionTwo windmills of height 50m and `40sqrt3 m` are on either side of the field. A person observes the top of the windmills from a point in between them. The angle of elevation was found to be `45^@ and 30^@`. Find the distance between the windmills.

View SolutionThe following table gives production yield per hectare of wheat of 100 farms of a village.
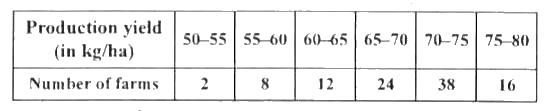
Change the distribution, and draw its ogive
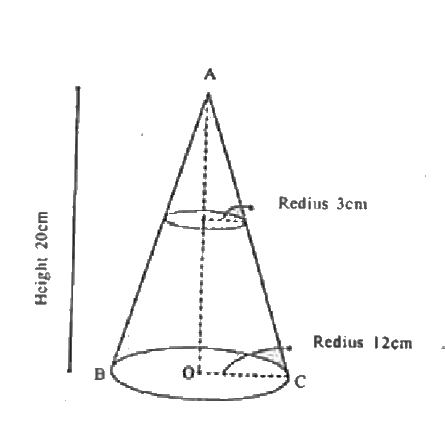
View SolutionA cone is having its base radius 12 cm and height 20 cm. If the top of this cone is cut in to form of a small cone of base radius 3cm is remove, then the remaining part of the solid cone becomes a frustum. Calculate the volume of the frustum.
View SolutionA milk tank is in the shape of a cyclinder with hemispheres of same radii attached to both ends of it as shown in figure. If the total height of the tank is 6m and the radius is 1m, calculate the maximum quantity of milk filled in the tank in litres. `(pi=(22)/(7))`
View SolutionThe sum of the `4^(th)` and `8^(th)` terms of an AP is 24 and the sum of the `6^(th)` and `10^(th)` terms is 44. Find the first three terms of the AP.
View SolutionProve that "In a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides".
View SolutionThe ages of two students A and B are 19 years and 15 years respectively. Find how many years it will take so that the product of their ages becomes equal to 480.
View SolutionIf the quadratic equation `(b-c)x_2+(c-a)x+(a-)=0` has equal roots, then show that `2b=a+c`.
View Solution
EXERCISE questions and complete solutions for chapter ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) of SUPER COMPANION MADE EASY of Class 10