Complete Solutions to EXERCISE 2.6 (OPTIONAL) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| SUBHASH PUBLICATION | EXERCISE 2.6 (OPTIONAL) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
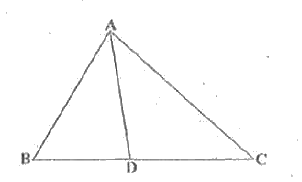
In Fig PS is the bisector of `angleQPR " of " DeltaPQR` . Prove that `(QS)/(SR)=(PQ)/(PR)`

View SolutionIn Fig . D is a point on hypotenuse AC of `DeltaABC, bot DM botBCand DNbot AB.` prove that :
`DM^(2)=DN.MC`
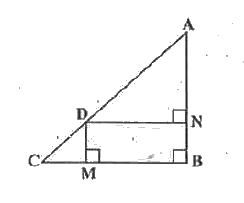
View SolutionIn Fig . D is a point on hypotenuse AC of `DeltaABC, bot DM botBCand DNbot AB.` prove that :
`DN^(2)=DM.AN`

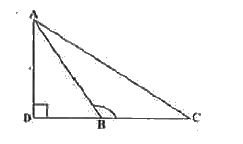
View SolutionIn Fig , ABC is a triangle in which `angleABCgt90^(@) and AD bot CB,` produced . Prove that `AC^(2)=AB^(2)+BC^(2)+2BC.BD`
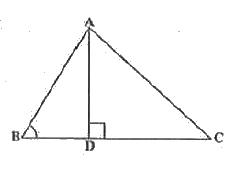
View SolutionIn Fig . ABC is a triangle in which `angleABClt90^(@)and AD botBC.` Prove that `AC^(2)=AB^(2)+BC^(2)-2BC.BD.`
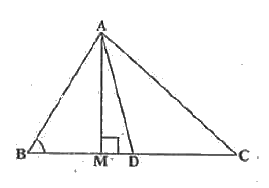
View SolutionIn Fig . AD is a median of a triangle `ABD and AM bot BC.` Prove that :
`AC^(2)=AD^(2)+BC.`
`DM+((BC)/(2))^(2)`
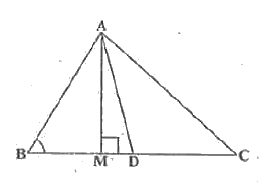
View SolutionIn Fig . AD is a median of a triangle `ABD and AM bot BC.` Prove that :
`AB^(2)=AD^(2)-BC.DM+((BC)/(2))^(2)`
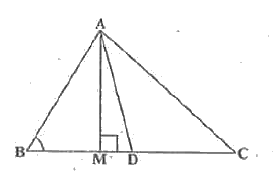
View SolutionIn Fig . AD is a median of a triangle `ABD and AM bot BC.` Prove that :
`AC^(2)+AB^(2)=2AD^(2)+1/2 BC^(2)`
View SolutionIf the diagonals of a parallelogram are equal, show that it is a rectangle.
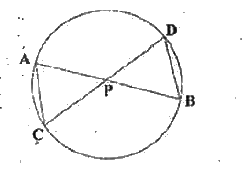
View SolutionIn Fig . two chords AB and CD intersect each other at the point P. prove that :
`DeltaAPC~DeltaDPB`

View SolutionIn Fig . two chords AB and CD intersect each other at the point P. prove that :
`AP.PB=CP.DP`
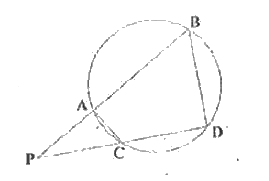
View SolutionIn Fig. two chords AB and CD of a circle intersect each other at the point P ( when produced ) outside the circle prove that
`DeltaPAC~DeltaPDB`

View SolutionIn Fig. two chords AB and CD of a circle intersect each other at the point P ( when produced ) outside the circle prove that
`PA.PB=PC.PD`
View SolutionIn Fig .D is a point on side BC of`DeltaABC` such that `(BD)/(CD) =(AB)/(AC)` prove that AD is the bisector of `angleBAC.`
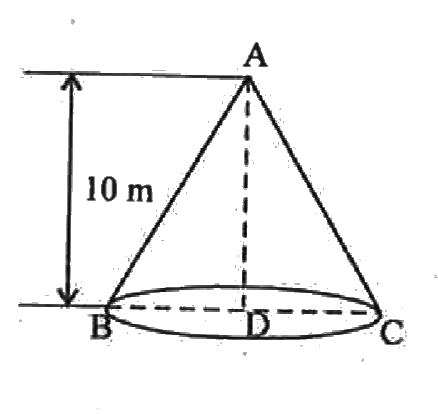
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find
slant height of the tent.
View Solution
EXERCISE 2.6 (OPTIONAL) questions and complete solutions for chapter TRIANGLES of SUPER COMPANION MADE EASY of Class 10