Complete Solutions to EXECRISE 1.3 of chapter RELATIONS AND FUNCTIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| SURA PUBLICATION | EXECRISE 1.3 |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
Let `f={(x, y)|x, yin N and y=2x}` be a relation on N. Find the domain, co-domain and range. Is this relation a function?
View SolutionLet `X={3, 4, 6, 8}`. Determine whether the relation `R={x, f(x)|xinX, f(x)=x^(2)+1}` is the function from X to N?
View SolutionGiven the function `f:x to x^(2)-5x+6`, evaluate
f(-1)
View SolutionGiven the function `f:x to x^(2)-5x+6`, evaluate
f(2a)
View SolutionGiven the function `f:x to x^(2)-5x+6`, evaluate
f(2)
View SolutionGiven the function `f:x to x^(2)-5x+6`, evaluate
f(x-1)
View SolutionA graph representing the function f(x) is given in figure it is clear that `f(9)=2`.
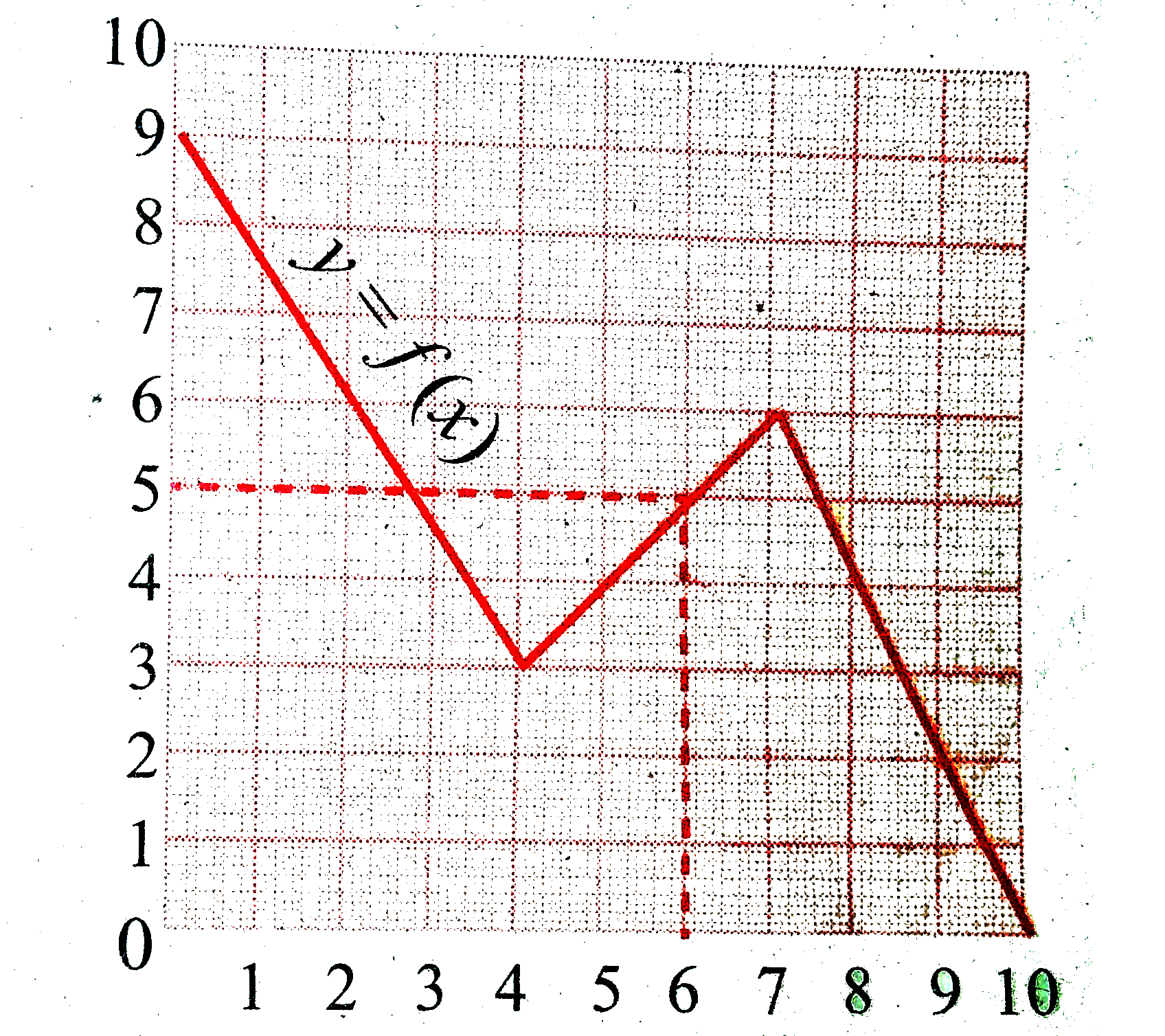
Find the following values of the function (a)f(0) (b)f(7) (c)f(2) (d)f(10)
View SolutionA graph representing the function f(x) is given in figure it is clear that `f(9)=2`.
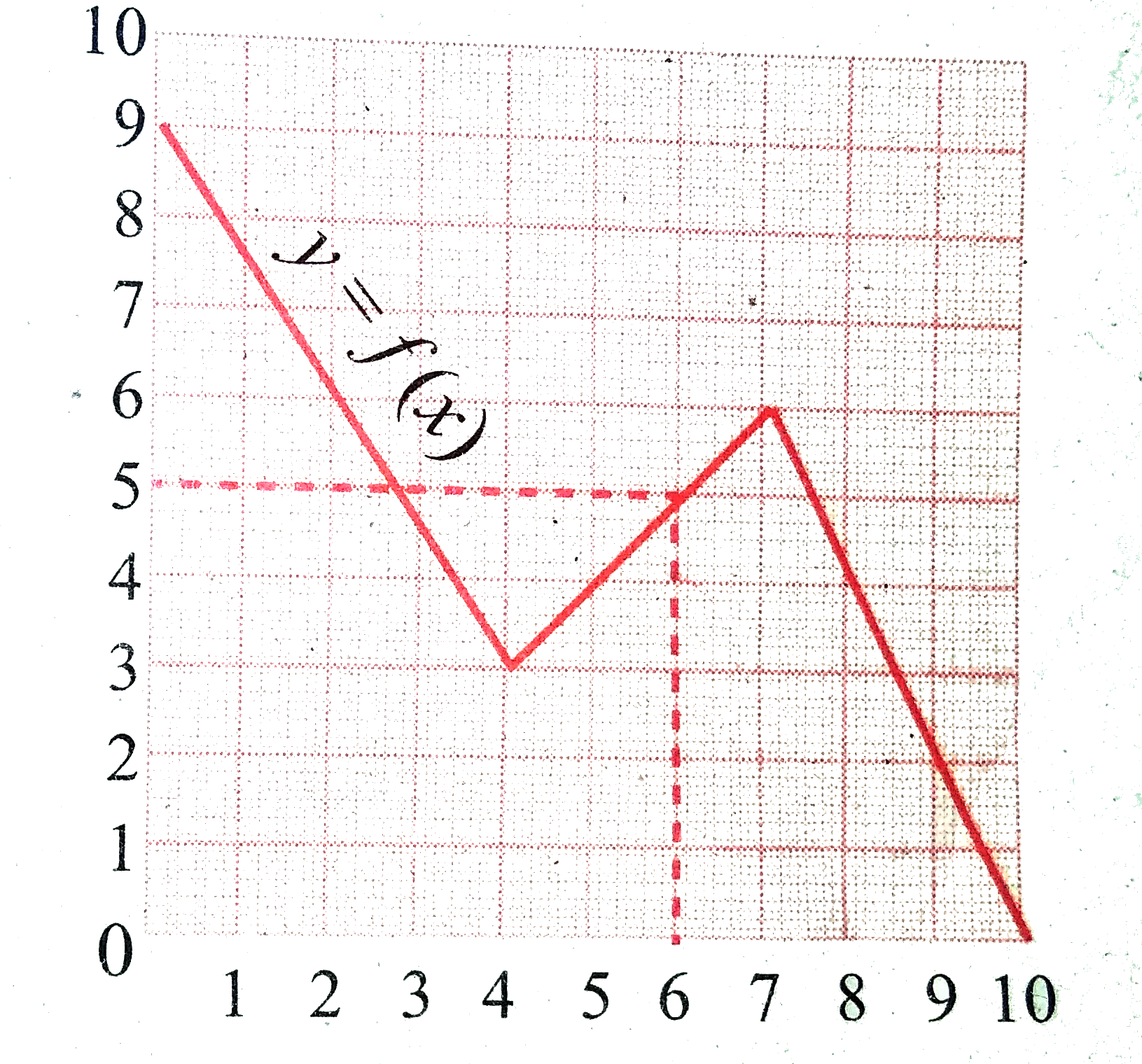
For what value of x is f(x)=1?
View SolutionA graph representing the function f(x) is given in figure it is clear that `f(9)=2`.

Describe the following (i) Domain (ii) Range.
View SolutionA graph representing the function f(x) is given in figure it is clear that `f(9)=2`.
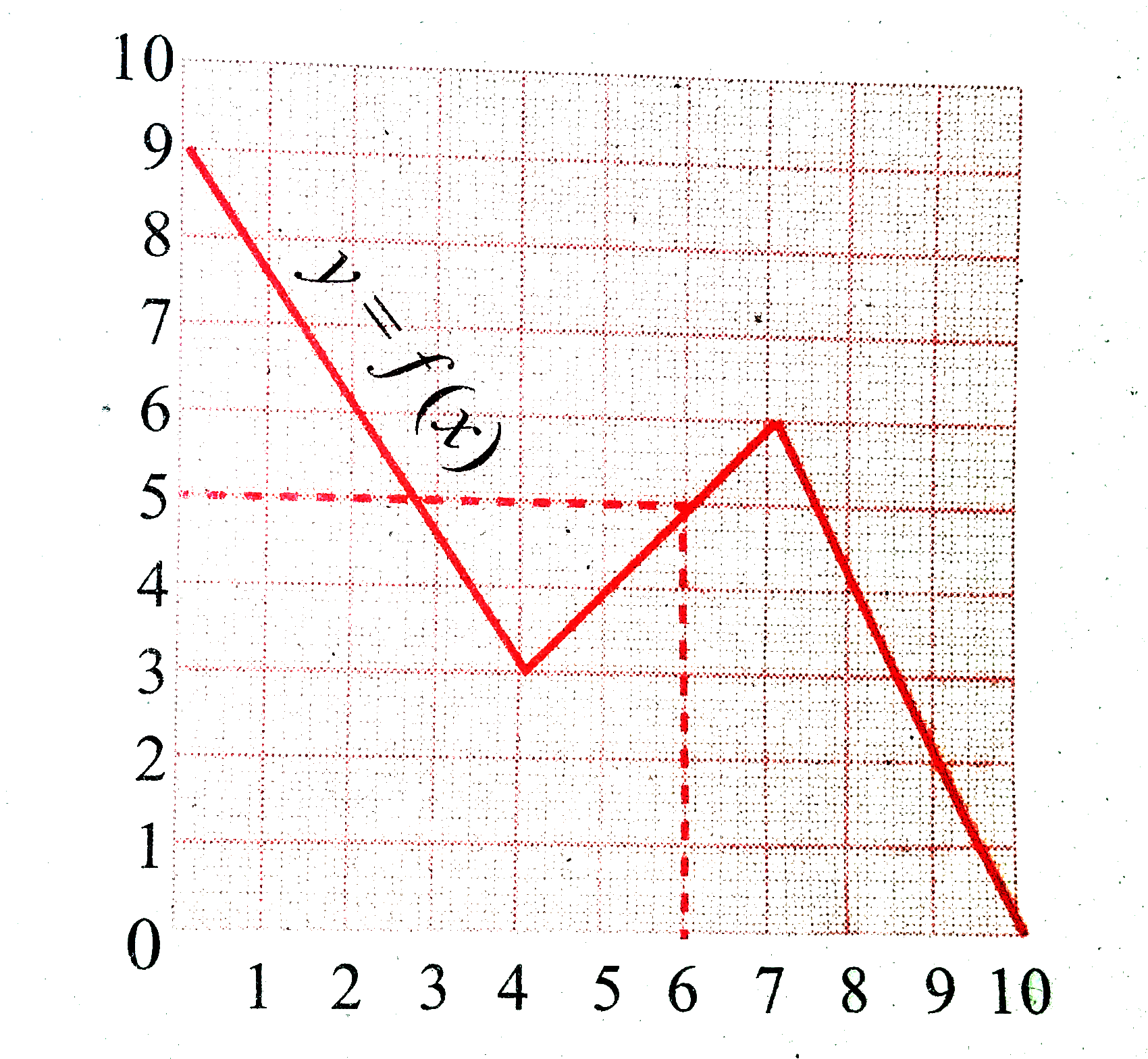
What is the image of 6 under f?
View SolutionLet `f(x)=2x+5`. If `xne0` then find `(f(x+2)-f(2))/(x)`
View SolutionA function is defined by `f(x)=2x-3`
Find `(f(0)+f(1))/(2)`.
View SolutionA function is defined by `f(x)=2x-3`
Find x such that `f(x)=0.`
View SolutionA function is defined by `f(x)=2x-3`
Find x such that `f(x)=x`.
View SolutionA function is defined by `f(x)=2x-3`
Find x such that `f(x)=f(1-x)`.
View SolutionAn open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown in figure. Express volume V of the box as a function of x.

View SolutionA function f is defined by `f(x)=3-2x`. Find x such that `f(x^(2))=(f(x))^(2).`
View Solutiona plane is flying at a speed of 500 km per hour. Express the distance d travelled by the plane as function of time t in hours.
View SolutionThe data in the adjcent table depicts the length of a woman's foreheads and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehead length (x) as `y=ax+b`, where a, b are constants.

Check if this relation is a functions.
View SolutionThe data in the adjcent table depicts the length of a woman's foreheads and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehead length (x) as `y=ax+b`, where a, b are constants.

Find a and b.
View SolutionThe data in the adjcent table depicts the length of a woman's foreheads and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehead length (x) as `y=ax+b`, where a, b are constants.

Find the height of a woman whose forehead length is 40 cm.
View SolutionThe data in the adjcent table depicts the length of a woman's foreheads and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehead length (x) as `y=ax+b`, where a, b are constants.

Find the length of forehead of a woman if her height is 53.3 inches.
View Solution
EXECRISE 1.3 questions and complete solutions for chapter RELATIONS AND FUNCTIONS of SURA MATHS (TAMIL ENGLISH) of Class 10