Complete Solutions to EXECRISE 1.4 of chapter RELATIONS AND FUNCTIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| SURA PUBLICATION | EXECRISE 1.4 |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
Determine whether the graph given below represents functions. Give reason for your answers concering each graph
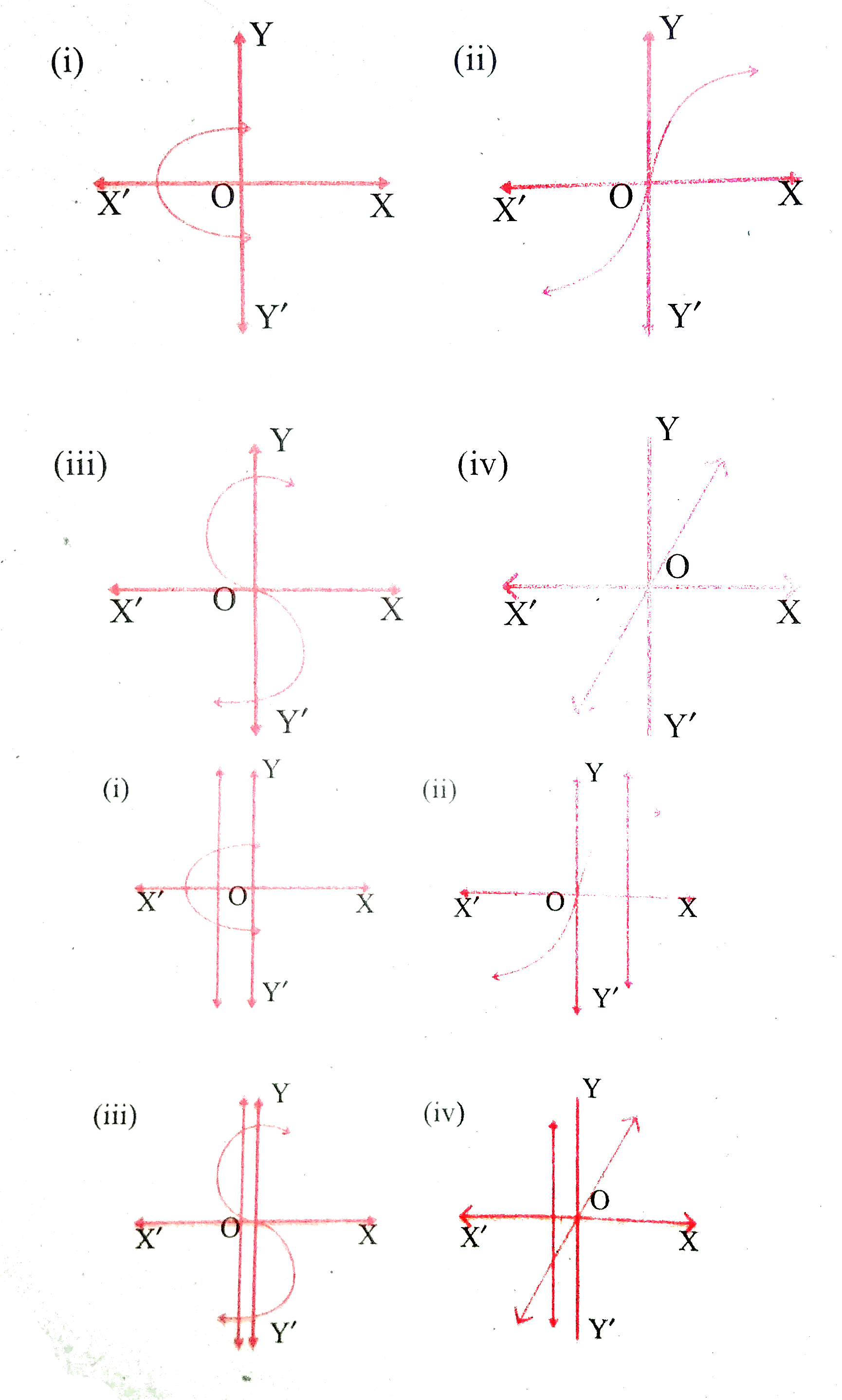
View SolutionLet: `f:A to B` be a function defined by `f(x)=(x)/(2)-1`. Where `A={2, 4, 6, 10, 12}, B={0, 1, 2, 4, 5, 9}. Represents f by
set of ordered pairs,
View SolutionLet: `f:A to B` be a function defined by `f(x)=(x)/(2)-1`. Where `A={2, 4, 6, 10, 12}, B={0, 1, 2, 4, 5, 9}. Represents f by
a table,
View SolutionLet: `f:A to B` be a function defined by `f(x)=(x)/(2)-1`. Where `A={2, 4, 6, 10, 12}, B={0, 1, 2, 4, 5, 9}. Represents f by
an arrow diagram diagram,
View SolutionLet: `f:A to B` be a function defined by `f(x)=(x)/(2)-1`. Where `A={2, 4, 6, 10, 12}, B={0, 1, 2, 4, 5, 9}. Represents f by
a graph,
View SolutionRepresent the function `f={(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)}` through
an arrow diagram
View SolutionRepresent the function `f={(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)}` through
a table form
View SolutionRepresent the function `f={(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)}` through
a graph
View SolutionShow that the function `f:N to N` defined by `f(x)=2x-1` is one-one but not onto.
View SolutionShow that the function `f:N toN` defined by `f(m)=m^(2)+m+3` is one-one function.
View SolutionLet `A={1, 2, 3, 4} and B=N`, Let `f:A to B` be defined by `f(x)=x^(3)` then,
Find the range of f.
View SolutionLet `A={1, 2, 3, 4} and B=N`. Let `f:A to B` to defined by `f(x)=x^(3)` then, identify the type of function
View SolutionIn each of the following cases state whether the functions is bijective or not. Justify your answer:
`f:R to R defined by `f(x)=2x+1`
View SolutionIn each of the following cases state whether the functions is bijective or not. Justify your answer:
`f:R to R` defined by `f(x)=3-4x^(2)`
View SolutionLet `A={-1, 1} and B={0, 2}`. If the functions `f:A to B` defined by `f(x)=ax+b` is an onto function? Find a and b.
View SolutionIf the function f is defined by
`f(x)={(x+2," if" xgt1), (2" if" `-1lexle1`), (x-1 " if" -3ltxlt-1):}` find the values of
f(3)
View SolutionIf the function f is defined by
`f(x)={(x+2," if" xgt1), (2" if" `-1lexle1`), (x-1 " if" -3ltxlt-1):}` find the values of
f(0)
View SolutionIf the function f is defined by
`f(x)={(x+2," if" xgt1), (2" if" `-1lexle1`), (x-1 " if" -3ltxlt-1):}` find the values of
f(-1.5)
View SolutionIf the function f is defined by
`f(x)={(x+2," if" xgt1), (2" if" `-1lexle1`), (x-1 " if" -3ltxlt-1):}` find the values of
f(2)+f(-2)
View SolutionA function `f:[-5, 9] to R` is defined as follows:
`f(x)={(6x+1" if" -5lexlt2`), (5x^(2)-1" if "2lexlt6), (3x-4" if " 6lexle9):}`
Find `f(-3)+f(2)`
View SolutionA function `f:[-5, 9] to R` is defined as follows:
`f(x)={(6x+1" if" -5lexlt2`), (5x^(2)-1" if "2lexlt6), (3x-4" if " 6lexle9):}`
Find `f(7)-f(1)`
View SolutionA function `f:[-5, 9] to R` is defined as follows:
`f(x)={(6x+1" if" -5lexlt2`), (5x^(2)-1" if "2lexlt6), (3x-4" if " 6lexle9):}`
Find `2f(4)+f(8)`
View SolutionA function `f:[-5, 9] to R` is defined as follows:
`f(x)={(6x+1" if" `-5lexlt2`), (5x^(2)-1" if "2lexlt6), (3x-4" if " 6lexle9):}`
Find `(2f(-2)-f(6))/(f(4)+f(-2))`
View SolutionThe distance S an object travles under the influence of gravity in time t seconds is given by `S(t)=(1)/(2)"gt"^(2)+at+b` where, (g is the acceleration due to gravity), a, b, are constants. Check if the function S(t) is one-one.
View SolutionThe function 't' which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)=F where `F=(9)/(5)C+32`.
Find t(0)
View SolutionThe function 't' which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)=F where `F=(9)/(5)C+32`.
Find t(28)
View SolutionThe function 't' which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)=F where `F=(9)/(5)C+32`.
Find t(-10)
View SolutionThe function 't' which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)=F where `F=(9)/(5)C+32`.
Find the value of C where t(C)=212
View SolutionThe function 't' which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)=F where `F=(9)/(5)C+32`.
Find the temperature when the Celsius value is equal to the Fahrenheit value.
View Solution
EXECRISE 1.4 questions and complete solutions for chapter RELATIONS AND FUNCTIONS of SURA MATHS (TAMIL ENGLISH) of Class 10