Complete Solutions to Chapter Assessment of chapter SIMILARITY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY |
| TARGET PUBLICATION | Chapter Assessment |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
Choose the correct alternative.
In the given figure, if BC = 3cm and BD = 7 cm , then `(A(DeltaABC))/(A(DeltaABD))`=
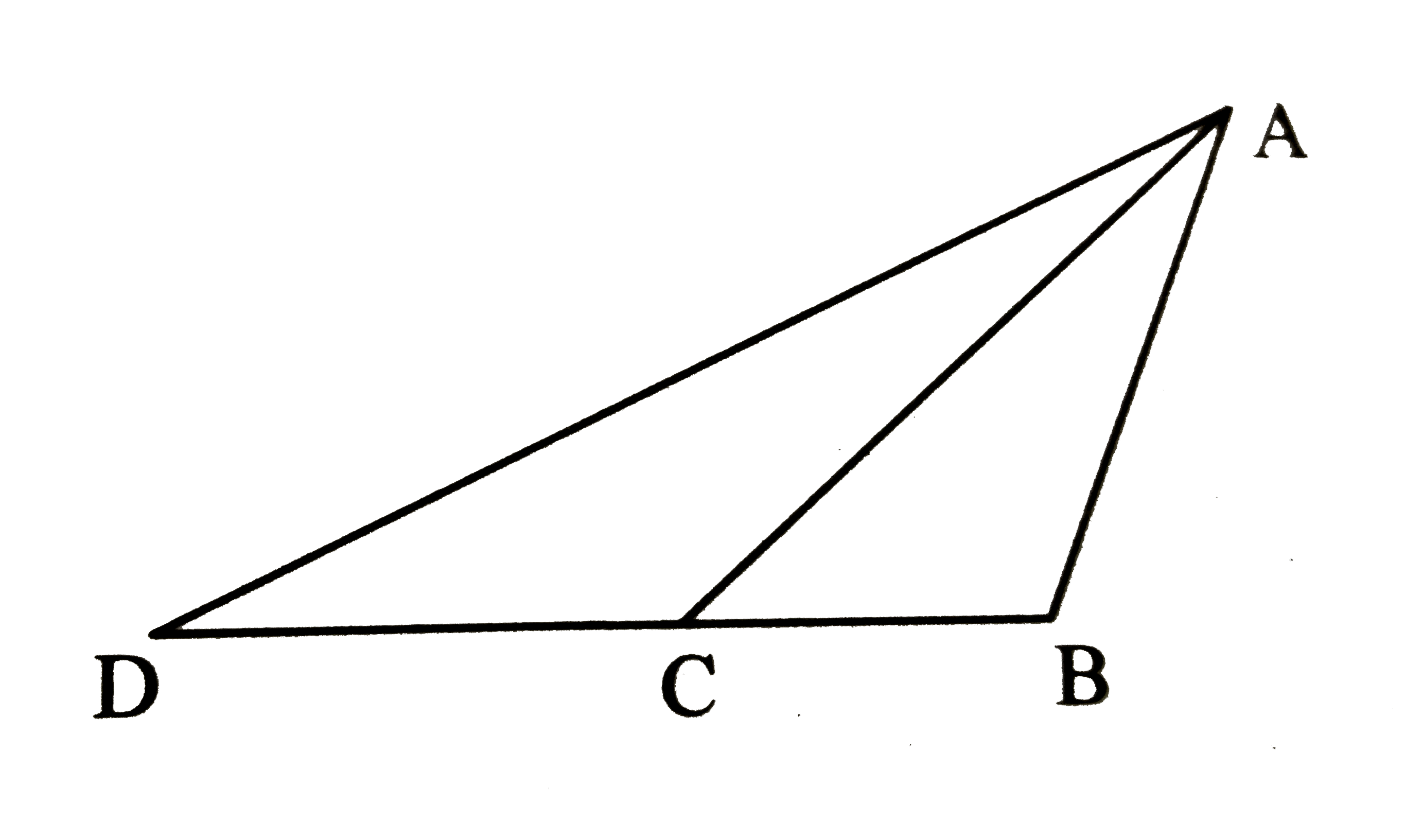
View SolutionChoose the correct alternative.
In the given figure, if seg PQ`abs()` BC, then `(A(DeltaBPQ))/(A(DeltaCQP))`=
(a) `(PQ)/(BC)` (b) `(PQ)/(QC)` (c) `(QC)/(BP)` (d) `1/1`
View SolutionChoose the correct alternative.
`DeltaABC and DeltaPQR` are equilateral triangles. If `A(DeltaABC) : A(DeltaPQR)` = 1 : 16, and AB = 2 cm, then what is the length of PR?
View SolutionChoose the correct alternative.
In the given figure, if seg PQ`abs()` RS `abs()`seg TU, and PR = 6, RT = 3, QS = 5, then what is the length of SU?

View Solution
In the given figure, ray PT is the bisector of `angleQPR.`
Find the value of x.

View Solution
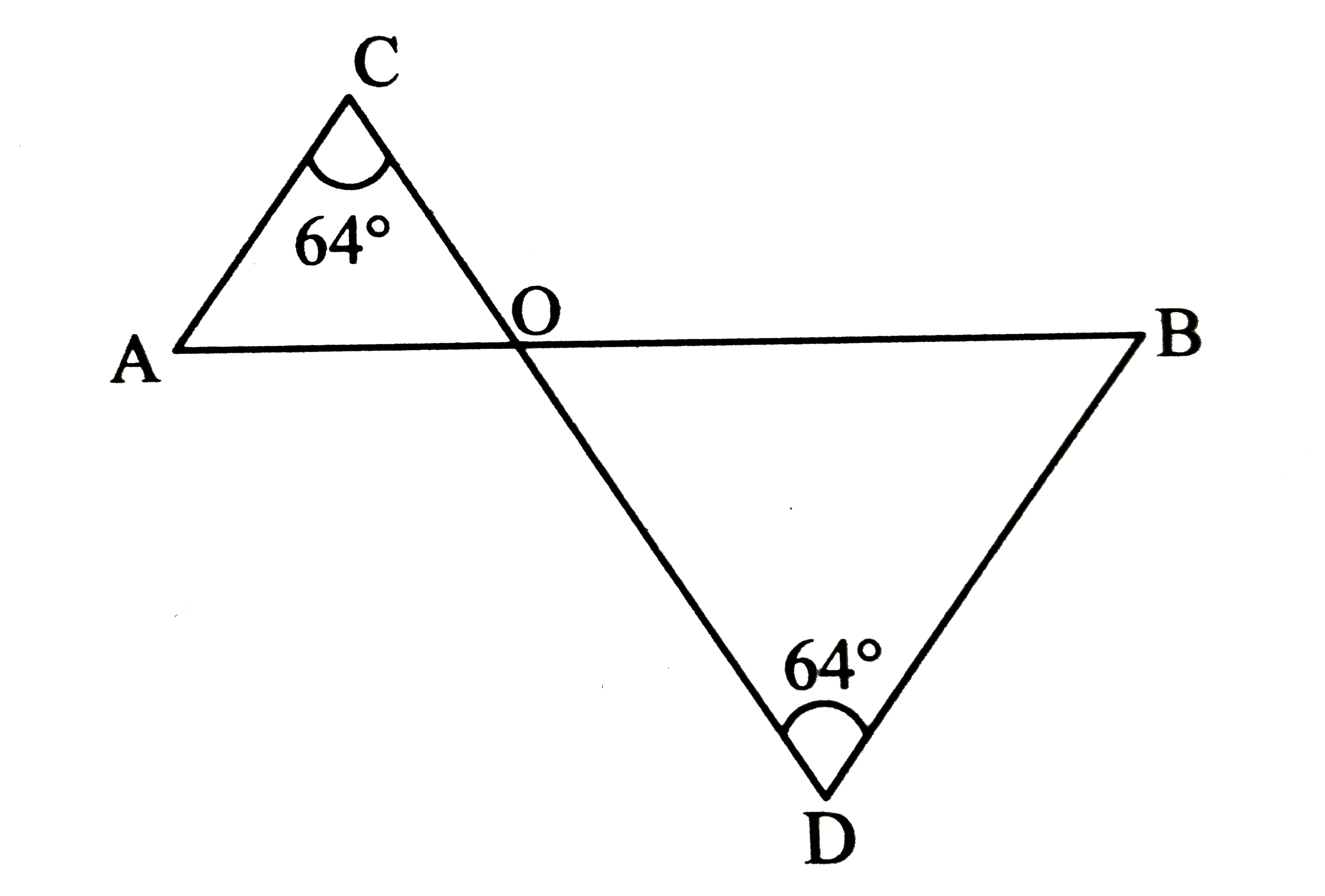
Are the triangle shown in the figure below similar? If so,
by which test of similarity?
View SolutionComplete the following activities
The areas of two triangle with same base are in proportion of their corresponding height. To prove the theorem, answer the following
a. Draw two triangles, give names of all points,show their bases.
b. Write ' given' and 'to prove' from the figures drawn.
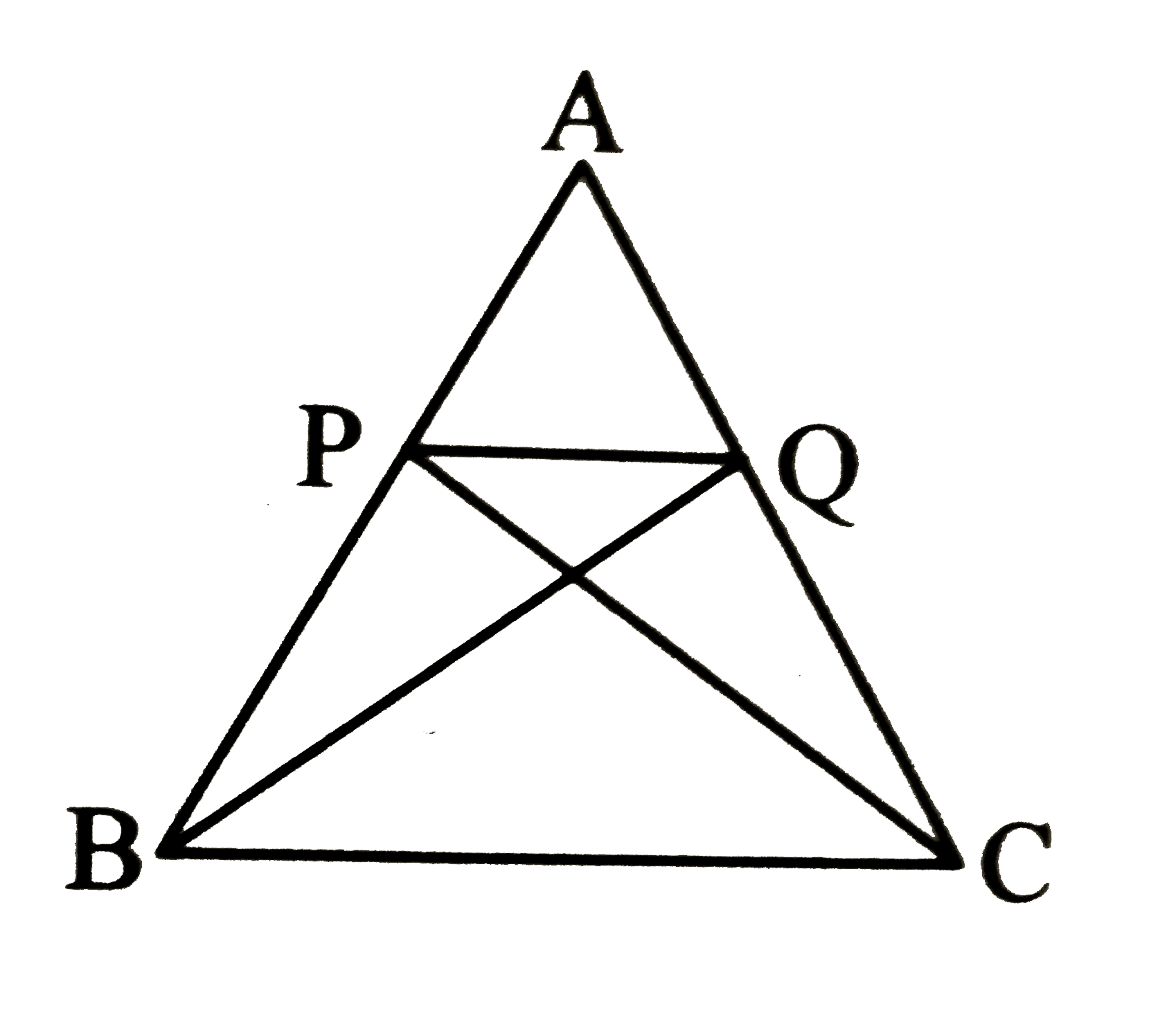
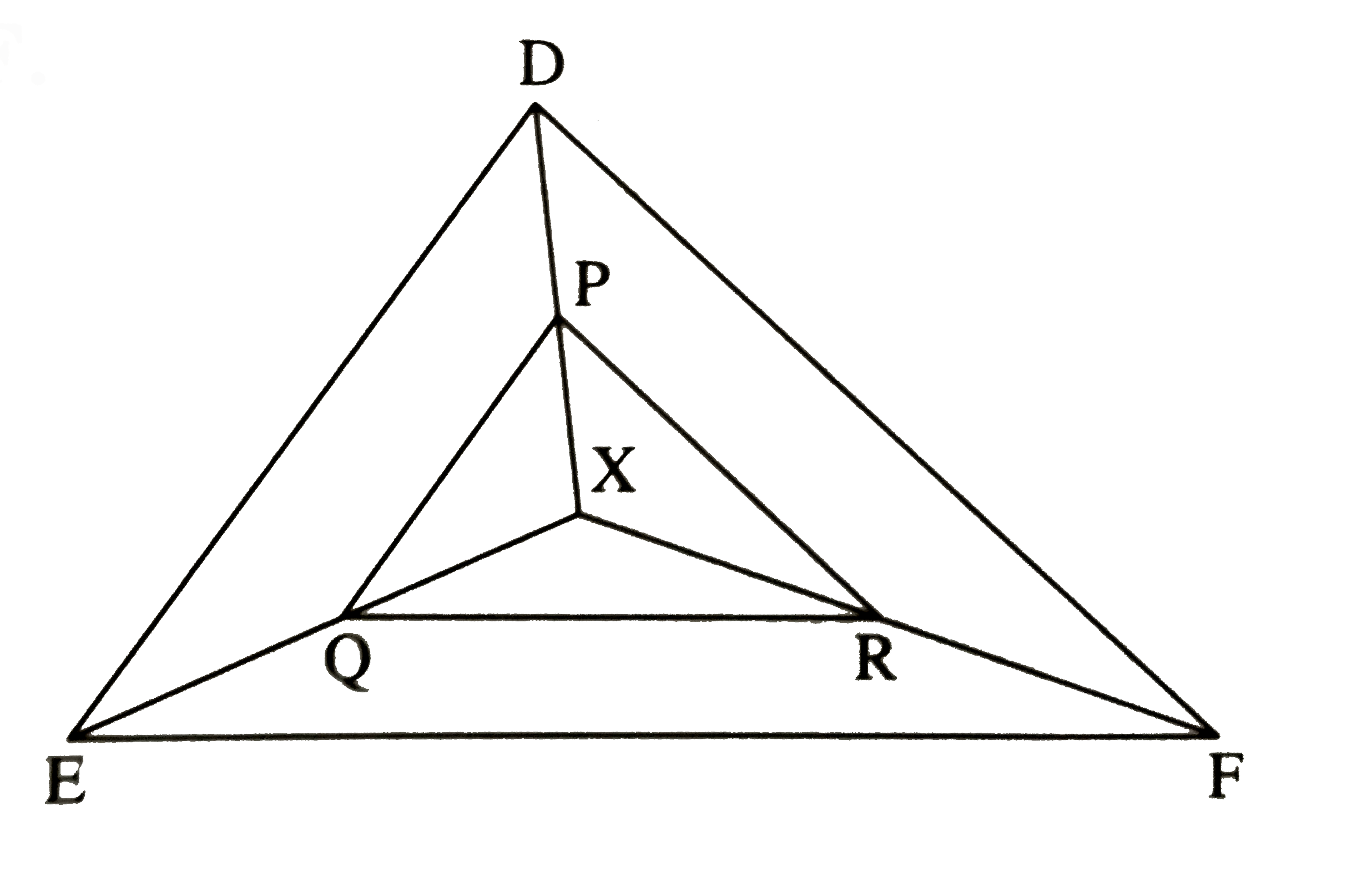
View SolutionIn the figure X is any point in the interior of triangle. Point X is joined
to vertices of triangle. Seg `PQ||` Seg DE, Seg `QR||` Seg EF.
Prove that Seg `PR||` Seg DF.
View SolutionIn the adoining figure, A - D - C and B - E -C . Seg DE `abs()` side AB. If AD = 5, DC = 3, BC = 6.4, then find BE.
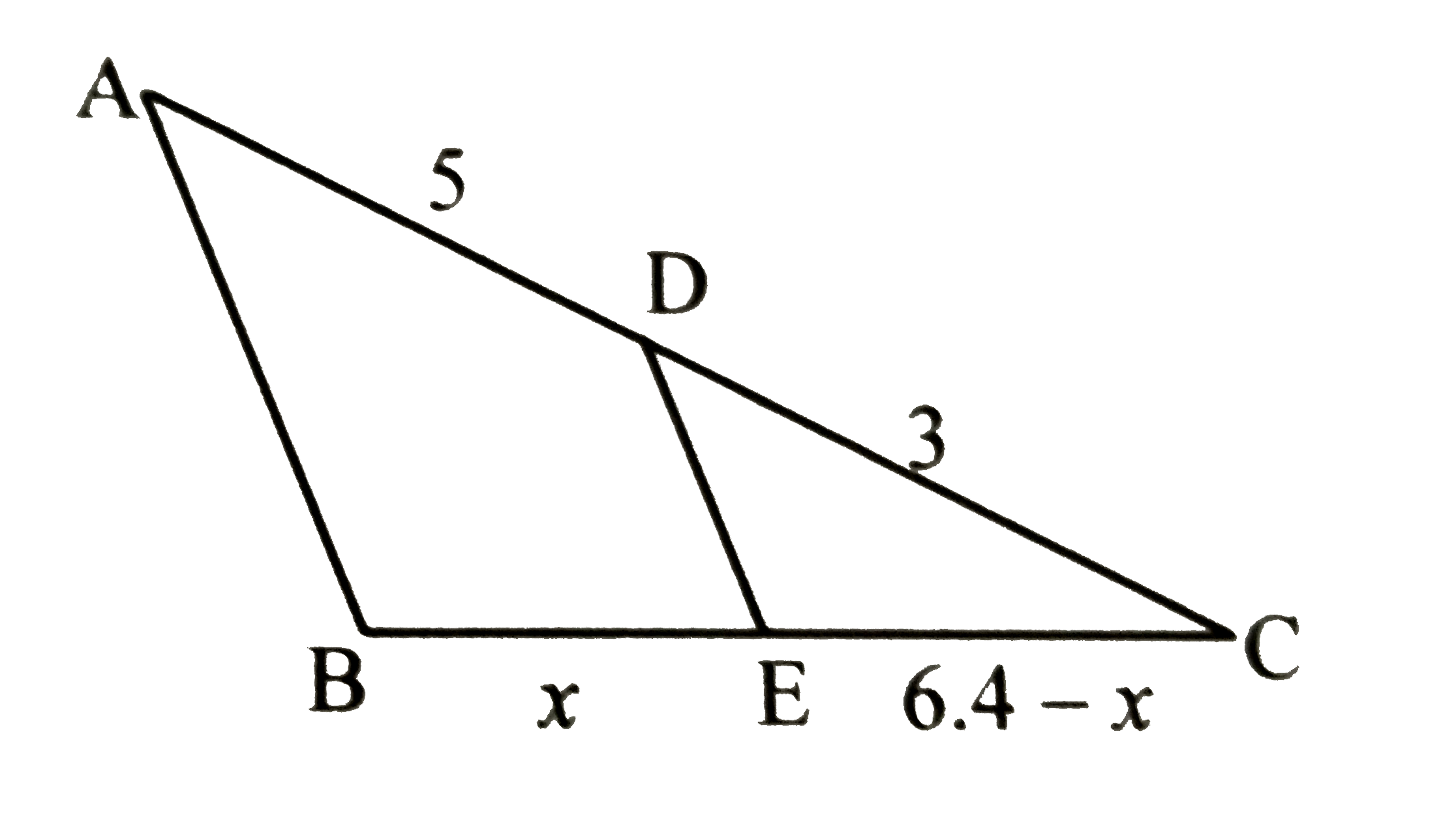
View SolutionThe ratio of the areas of two triangles with equal height is 3 : 4.
Base of the smaller triangle is 15 cm. Find the corresponding base
of the large triangle.
View Solution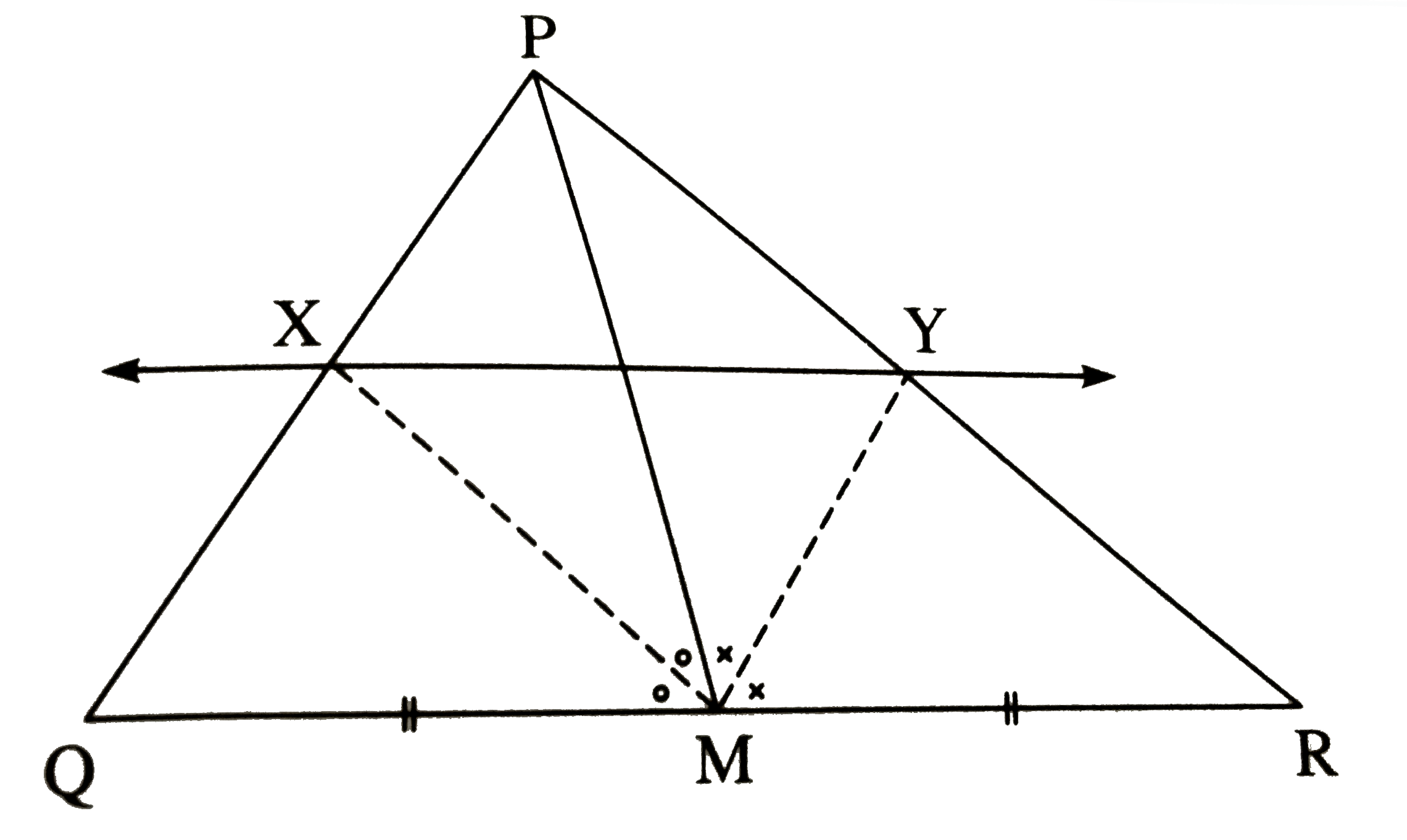
In `DeltaPQR` seg PM is a median. Angle bisectors of `/_PMQ` and `/_PMR` interesect `side PQ` and `side PR` in points `X` and `Y` respectively. Prove that `XY||QR`.
View SolutionDiagonals of a quadrilateral ABCD intersect in point Q. if 2 QA = QC,
2 QB = QD, then prove that DC = 2 AB.
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides
in the same proportion".
View SolutionSlove the following questions.
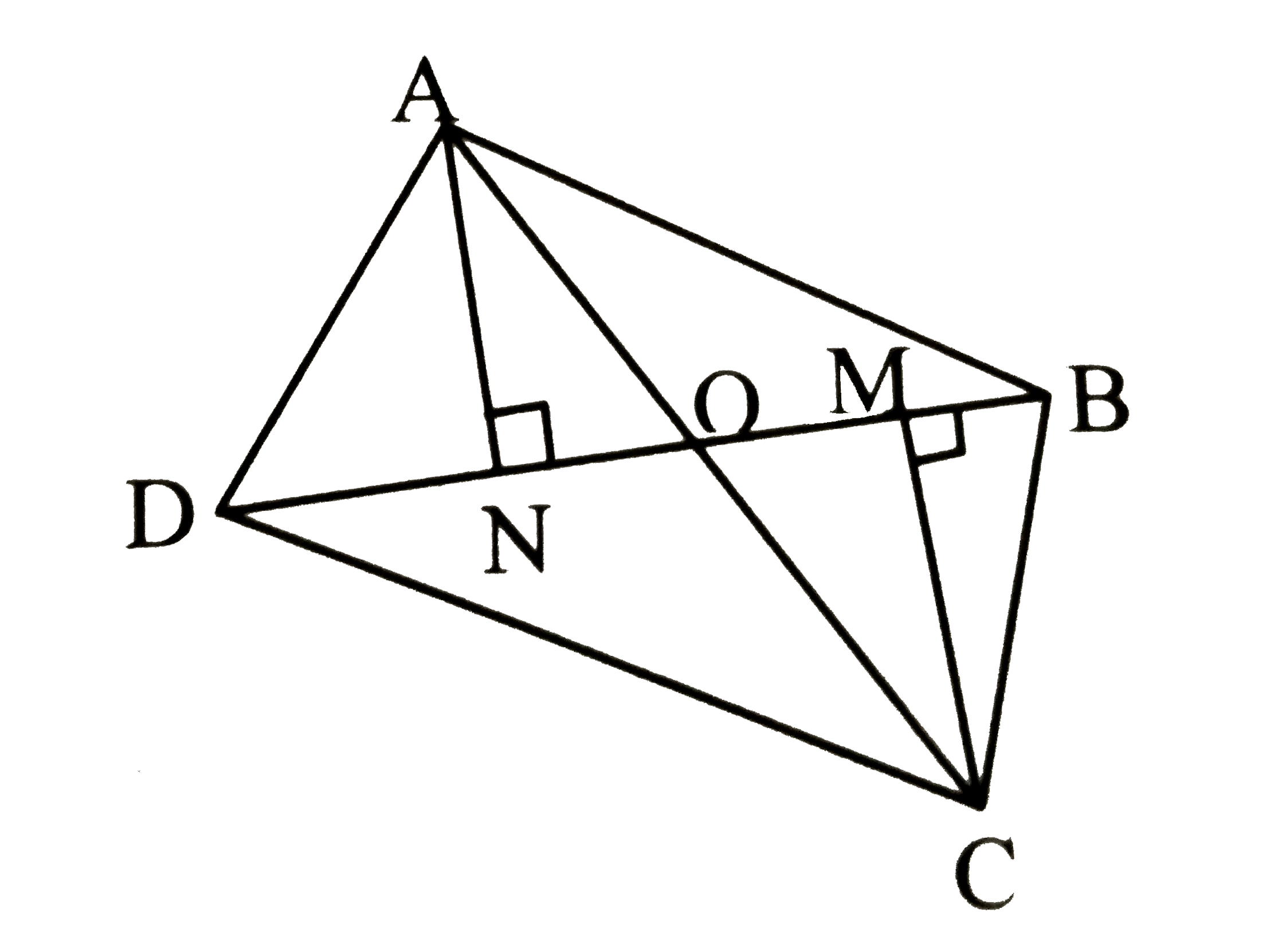
In the figure, `DeltaADB and DeltaCDB` are drawn on the same
base BD.if AC and BD intersect at O,
then prove that `(A(DeltaADB))/(A(DeltaCDB)) = (AO)/(CO).`
View Solution
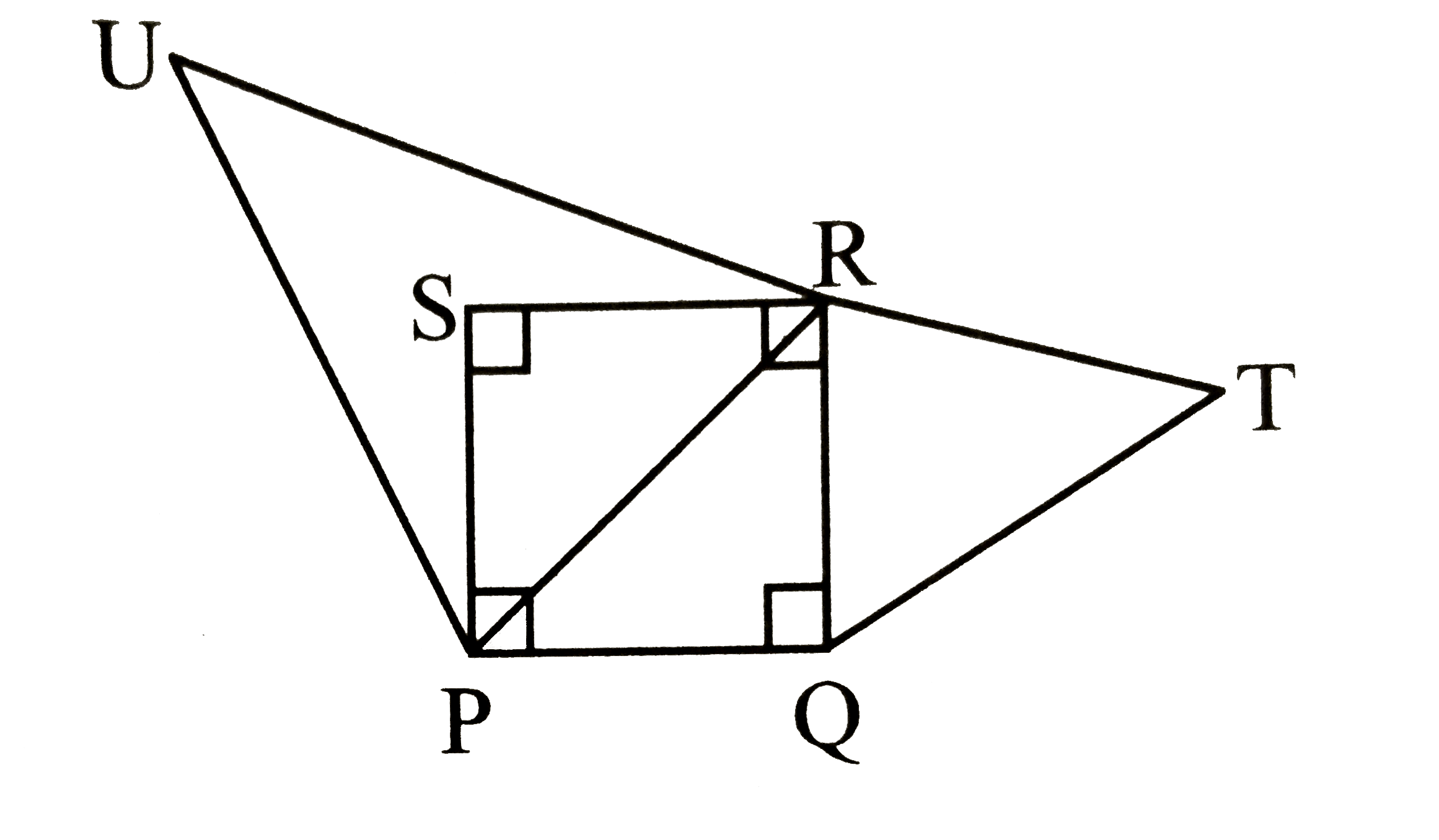
In the given figure, `squarePQRS` is a square. If `DeltaQRT and DeltaPRU` are similar to each other, then prove that `A(DeltaQRT) = 1/2 A(DeltaPRU)`.
View Solution
Prove that for a given correspondence, if three angles of one triangles are congruent to the corresponding three angles of the other triangle, then the two triangles are similar.
View SolutionProve:In a triangle the angle bisector divides the side opposite to the angle in the ratio of the remaining sides.
View Solution
Chapter Assessment questions and complete solutions for chapter SIMILARITY of TARGET PUBLICATION of Class 10
All Exercises from TARGET PUBLICATION Class 10 MATHS SIMILARITY
- Activites for Practice
- Additonal Problems for Practice( Basid on Practice Set 1.1)
- Additonal Problems for Practice(Based on Practice Set 1.2)
- Additonal Problems for Practice(Based on Practice Set 1.3)
- Additonal Problems for Practice(Based on Practice Set 1.4)
- Chapter Assessment
- Fill in the properly. State the reason.
- Multiple Choice Questions
- Practice Set 1.1
- Practice Set 1.2
- Practice Set 1.3
- Practice Set 1.4
- Problem Set - 1
- Textual Activity