Complete Solutions to Problem Set - 1 of chapter SIMILARITY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY |
| TARGET PUBLICATION | Problem Set - 1 |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
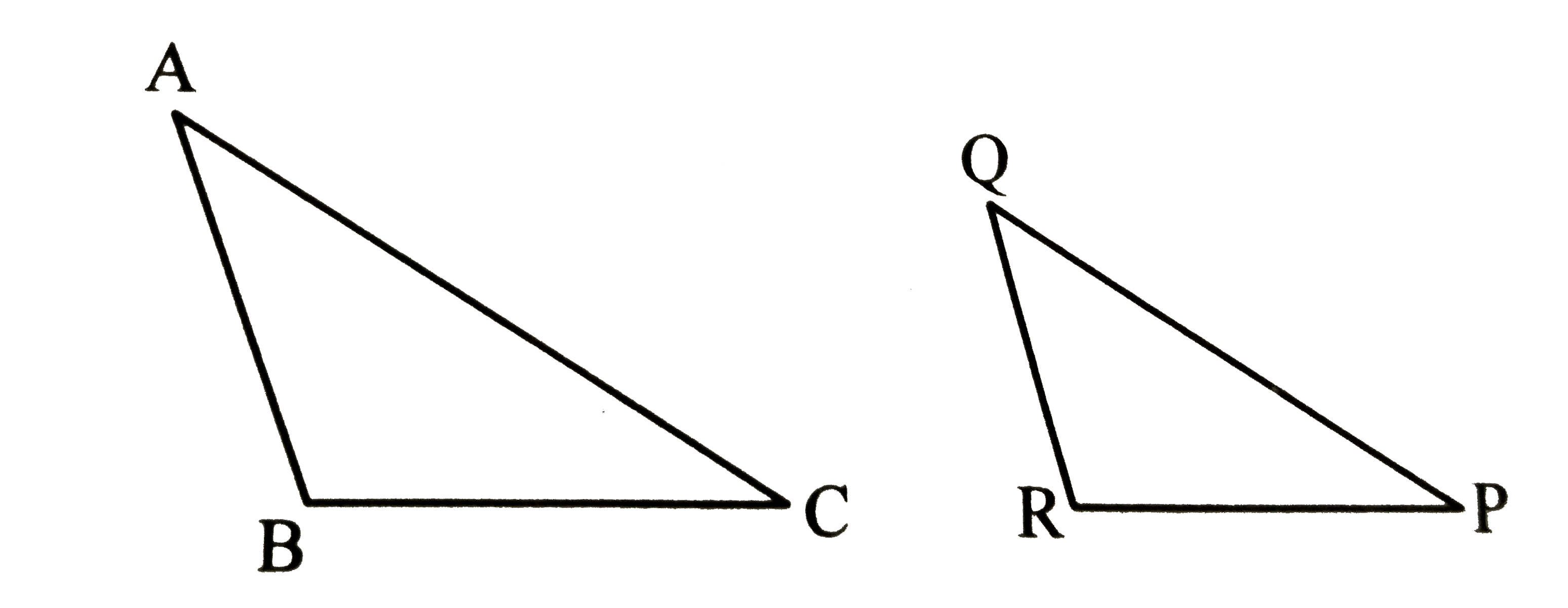
In `DeltaABC and DeltaPQR`, in a one to one correspondence.
`(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then
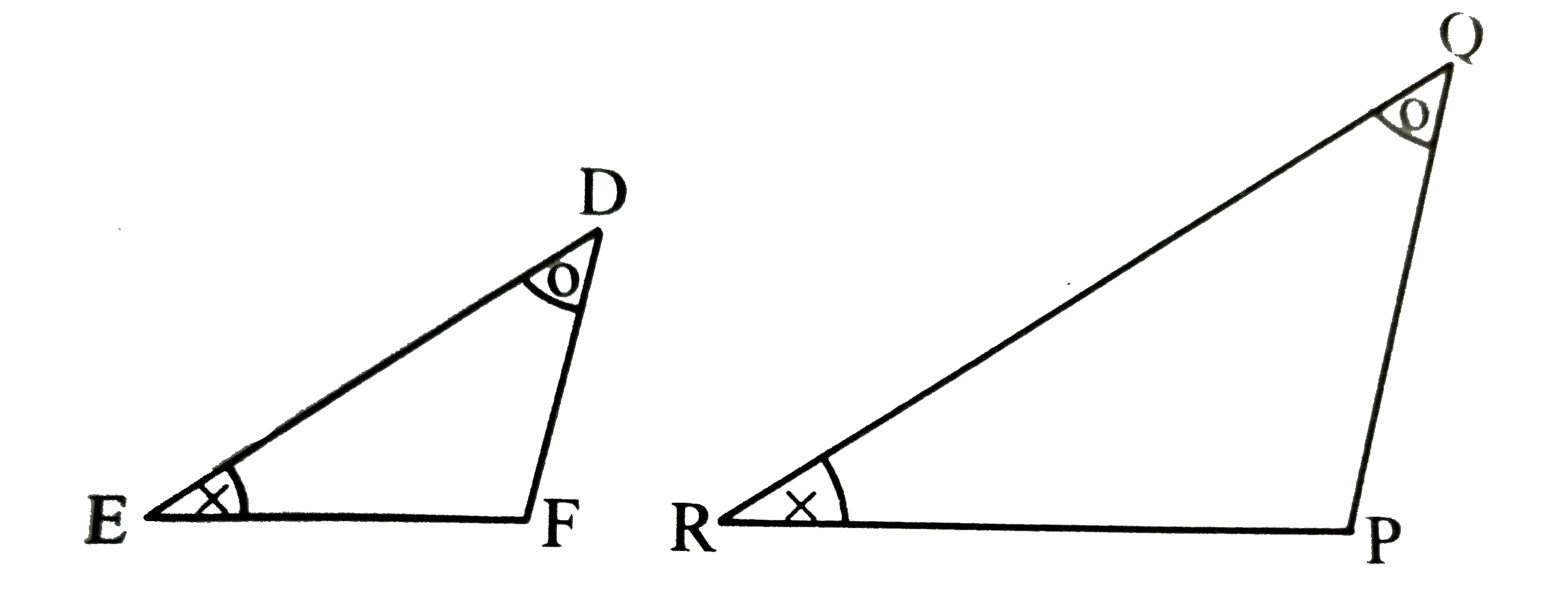
View SolutionIf in `DeltaDEF and DeltaPQR, angleD cong angleQ, angleR cong angleE`, then which
of the following statements is false?
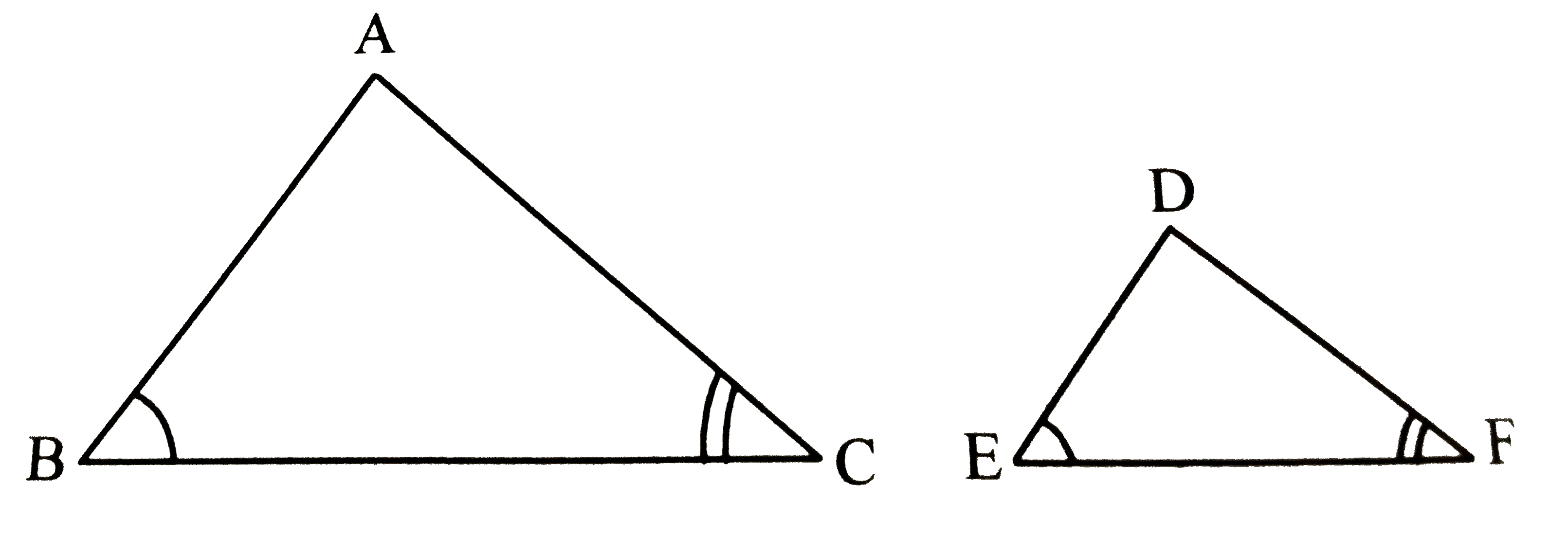
View SolutionIn `DeltaABC and DeltaDEF, " " angleB = angleE, angleF = angleC` and
`AB = 3 DE`, then which of the statements regarding the two
triangles is true?
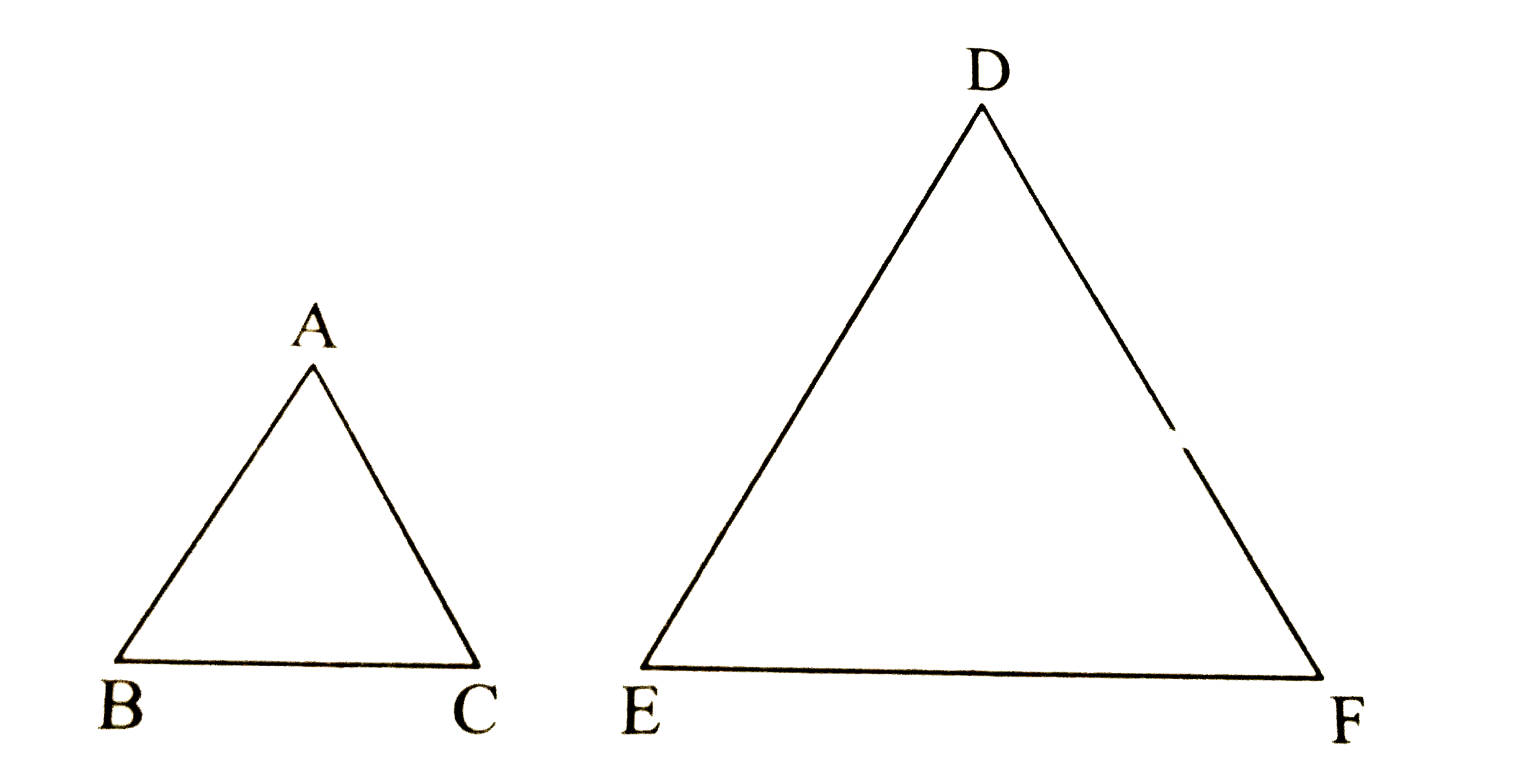
View Solution`DeltaABC` and `DeltaDEF` are equilateral triangles, `A(DeltaABC) : A(DeltaDEF)= 1 :2`.
If `AB=4` then what is the length of `DE`?
View SolutionIn the adjoining figure, seg XY `abs()`seg BC, then which of the following statements is true?
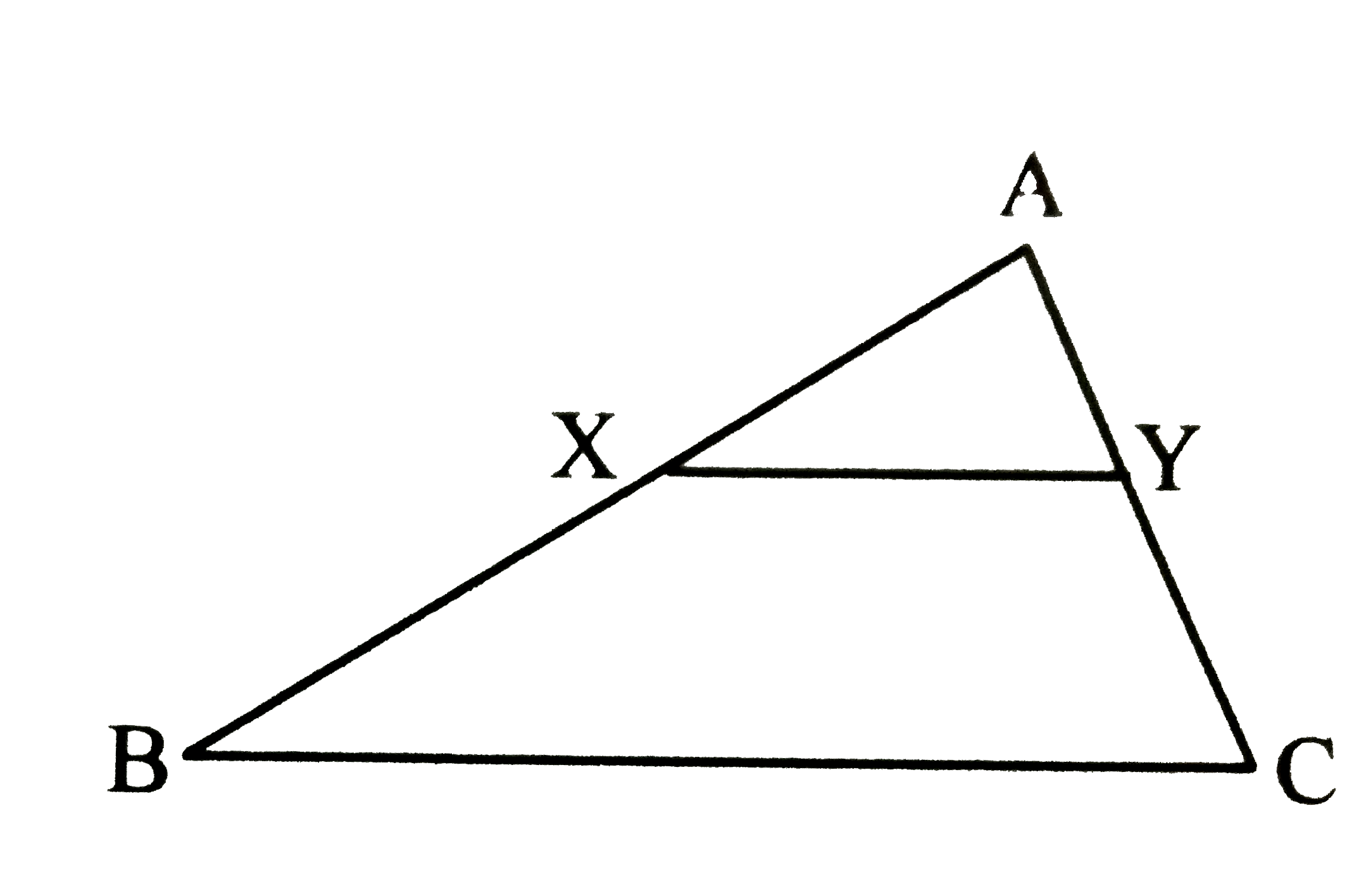
View SolutionIn `DeltaABC`, `B - D - C and BD = 7, BC = 20`, then
find the ratio.
`(A(DeltaABD))/(A(DeltaADC))`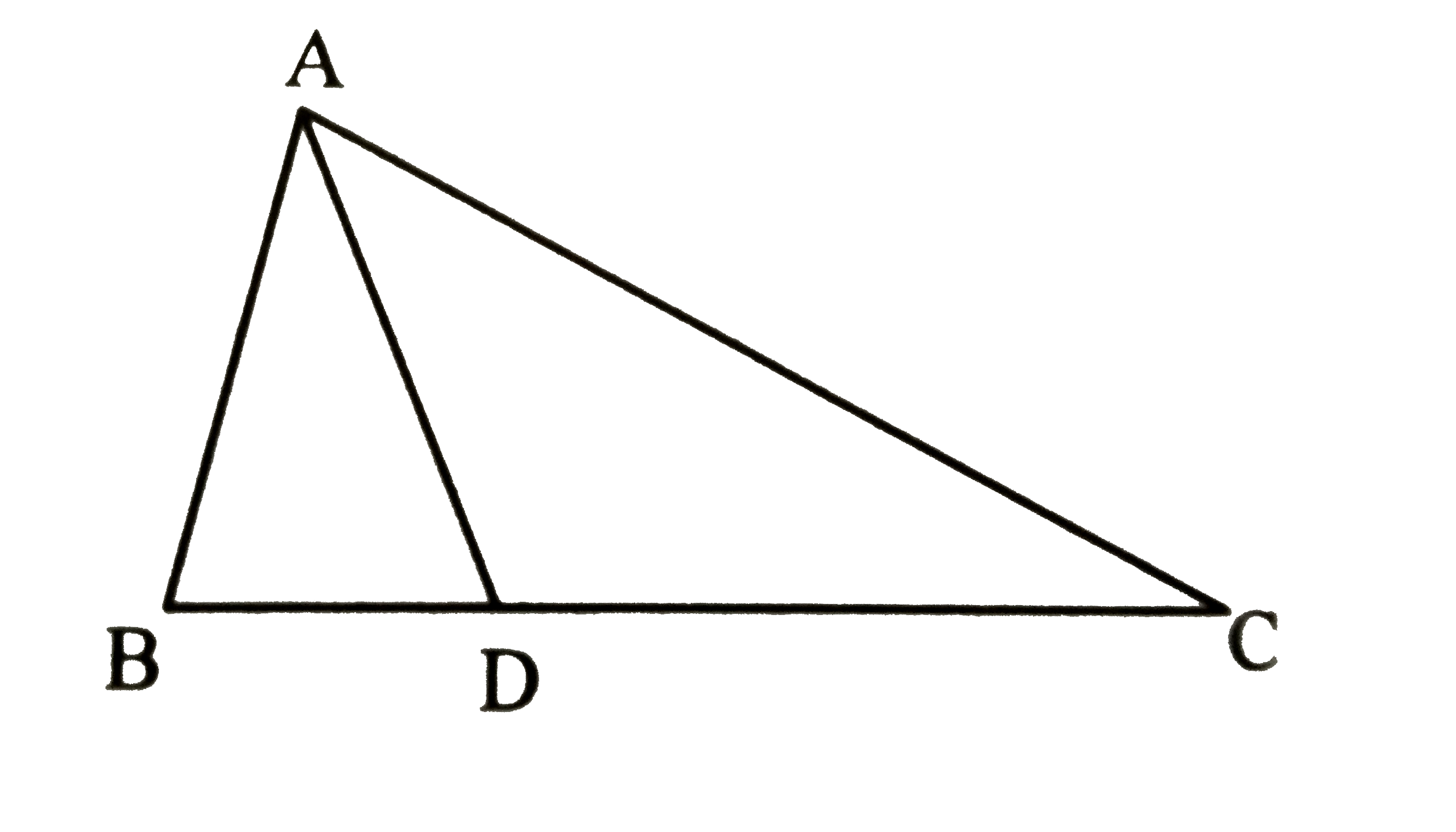
View SolutionIn `DeltaABC`, `B - D - C and BD = 7, BC = 20`, then
find the ratio
`(A(DeltaABD))/(A(DeltaABC))`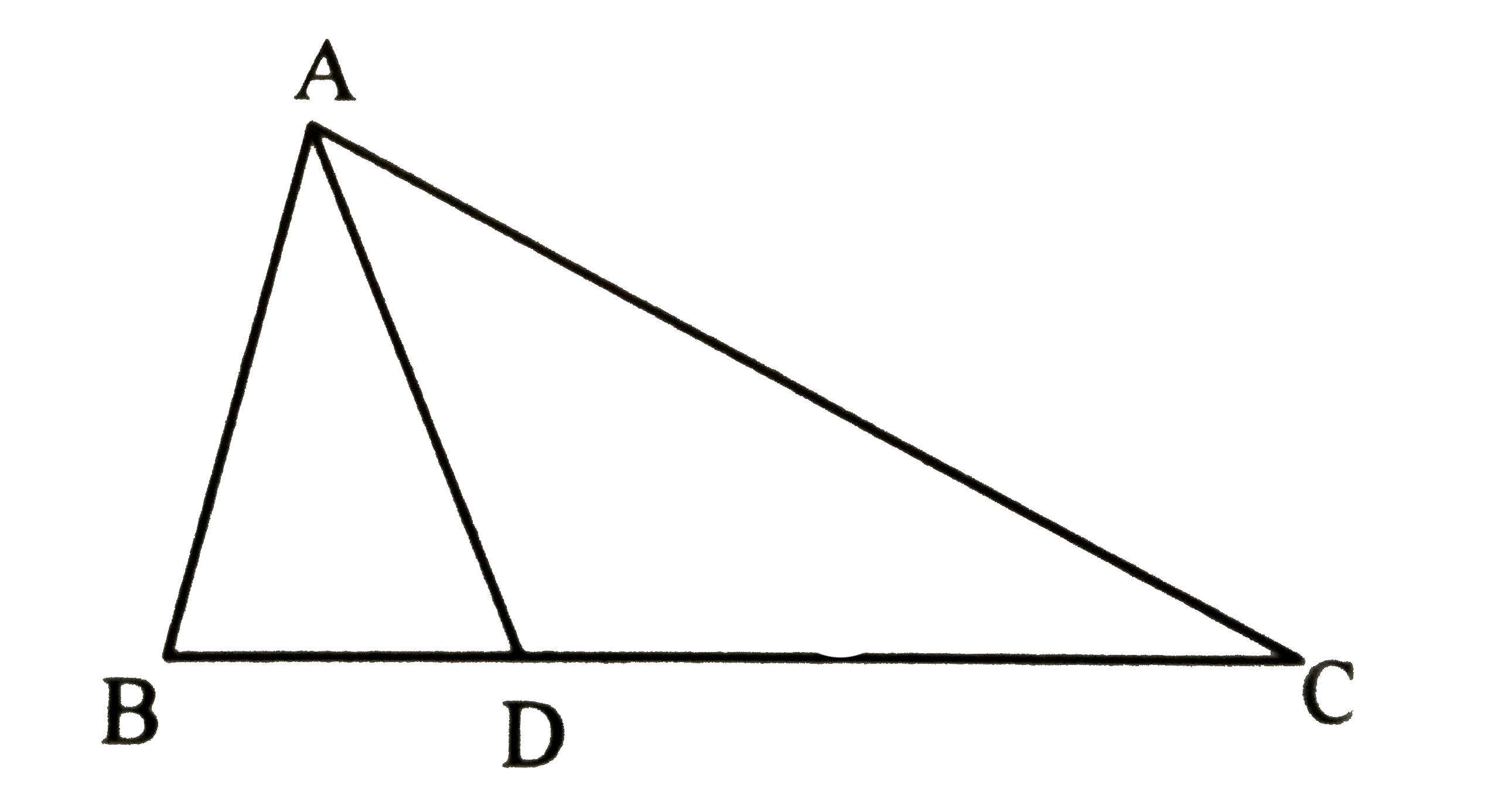
View SolutionIn `DeltaABC`, `B - D - C and BD = 7, BC = 20`, then
find following rations.
`(A(DeltaADC))/(A(DeltaABC))`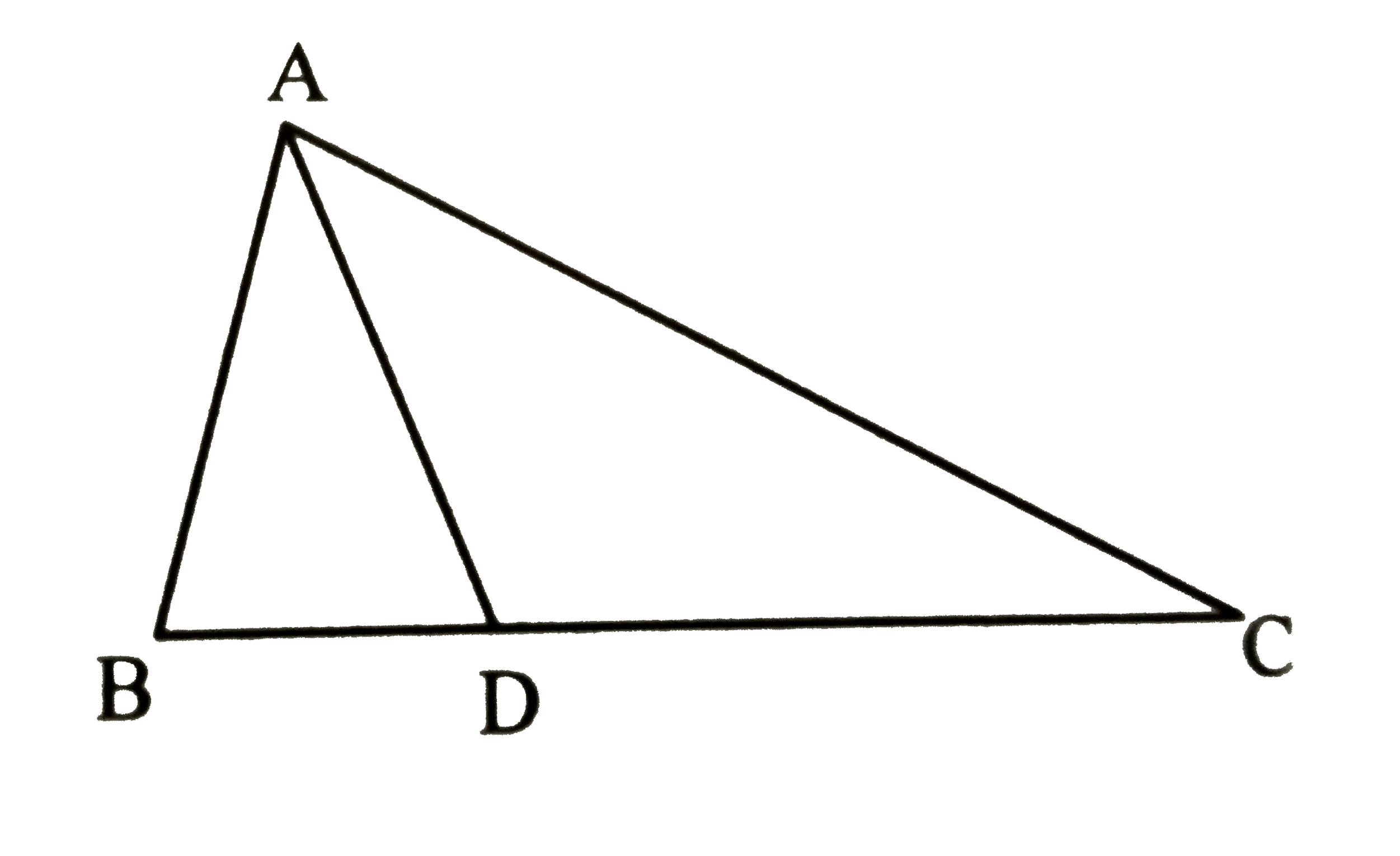
View SolutionRatio of areas of two triangles with equal height is 2:3. If base of smaller triangle is 6 cm then find the corresponding base of the bigger triangle.
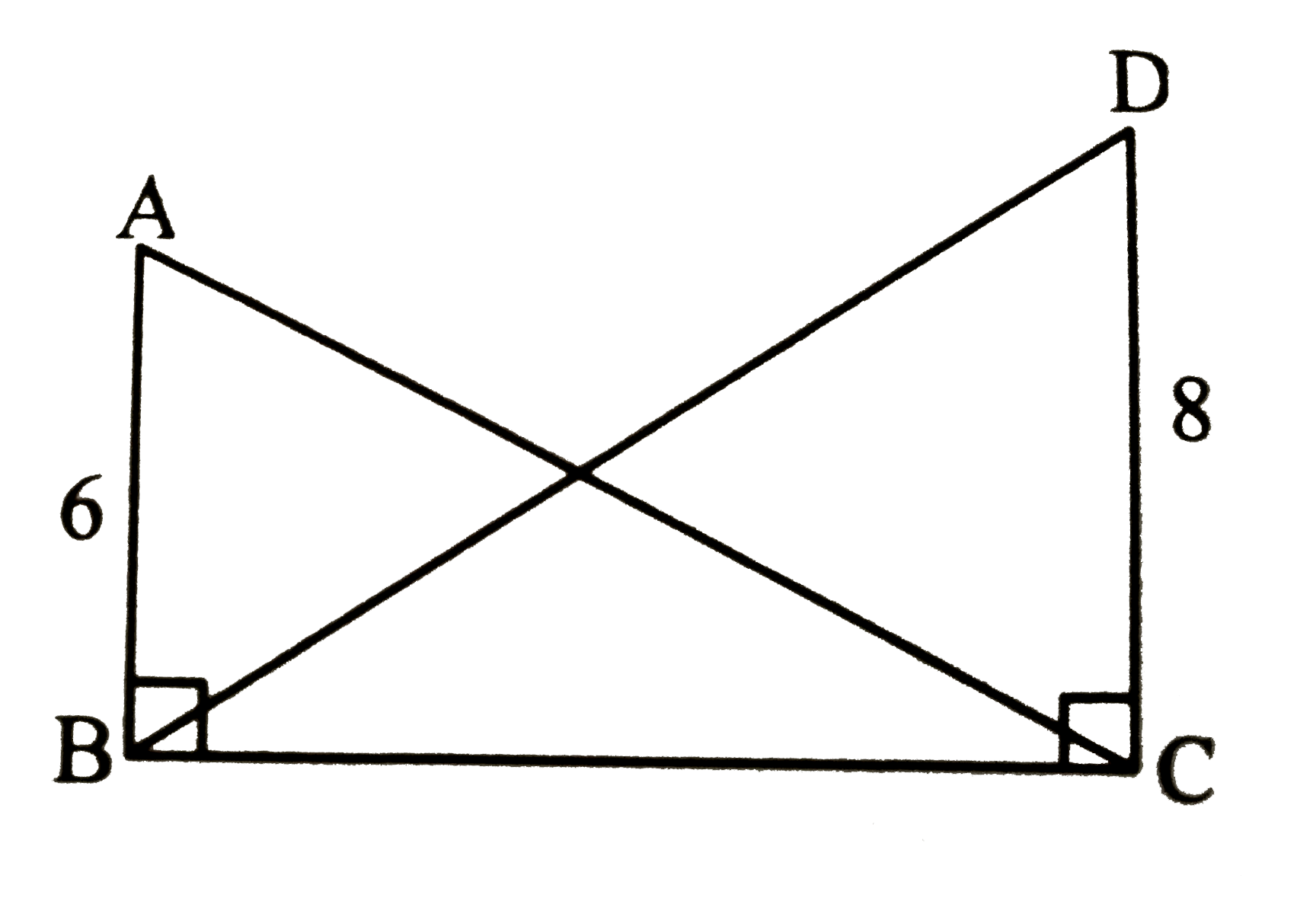
View SolutionIn the adjoining figure, `angleABC = angleDCB = 90^@ , AB = 6 , DC = 8,` then
`(A(DeltaABC))/(A(DeltaDCB))` = ?
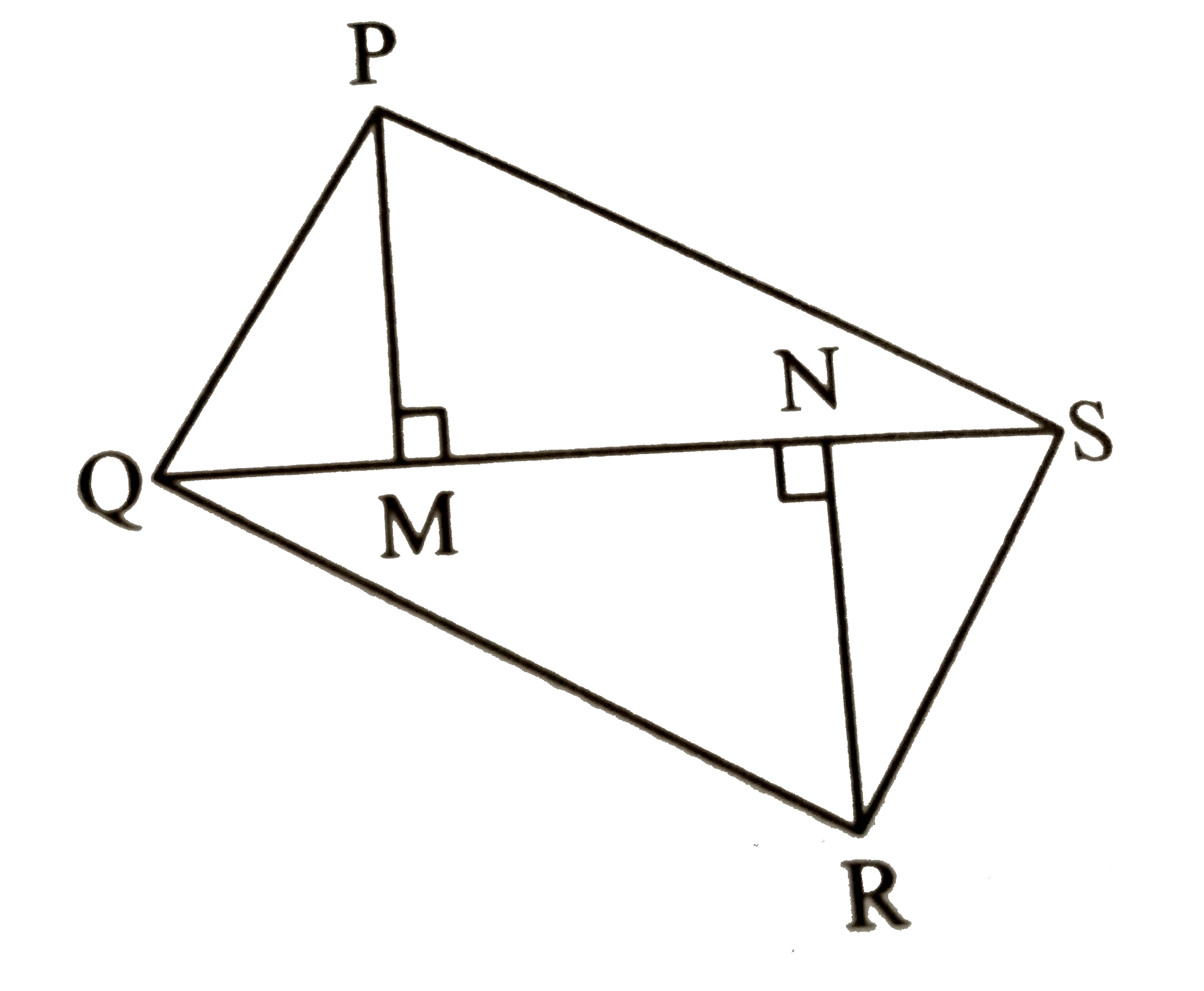
View SolutionIn the adjoining figure, PM = 10 cm, `A(DeltaPQS)` = `100 sq. cm`,
`A(DeltaQRS) = 110 sq. cm`, then find `NR`.
View Solution`DeltaMNT ~ DeltaQRS`. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio
`(A(DeltaMNT))/(A(DeltaQRS))`.
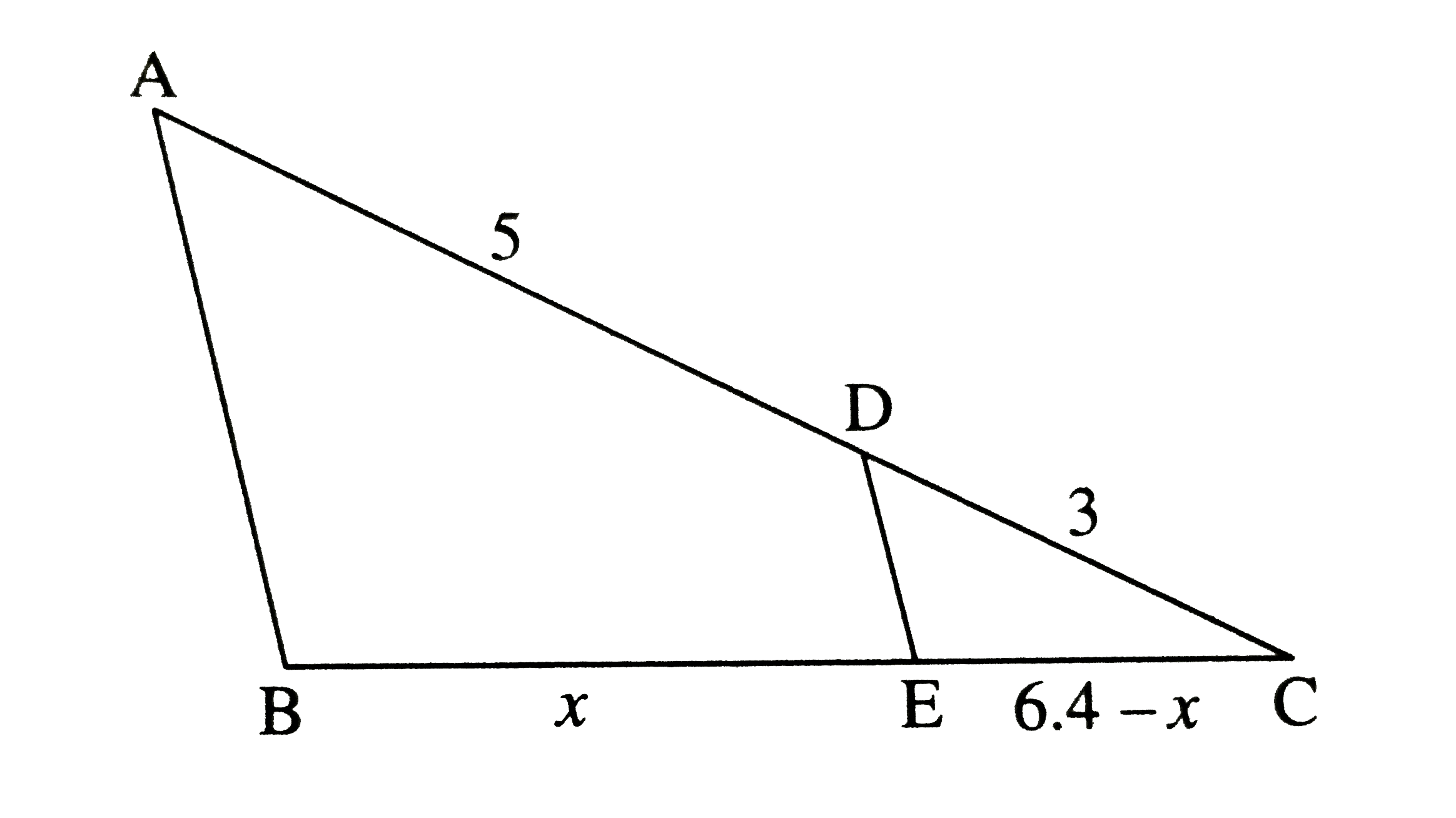
View SolutionIn the figure `A-D-C` and `B-E-C` seg `DE||` side AB. If `AD=5, DC=3, BC=6.4` then find BE.
View SolutionIn the adjoining figure, seg PA , seg QB, seg RC and seg SD are perpendicular to line AD. AB = 60, BC = 70, CD = 80, PS = 280, then
find PQ, QR and RS.

View Solution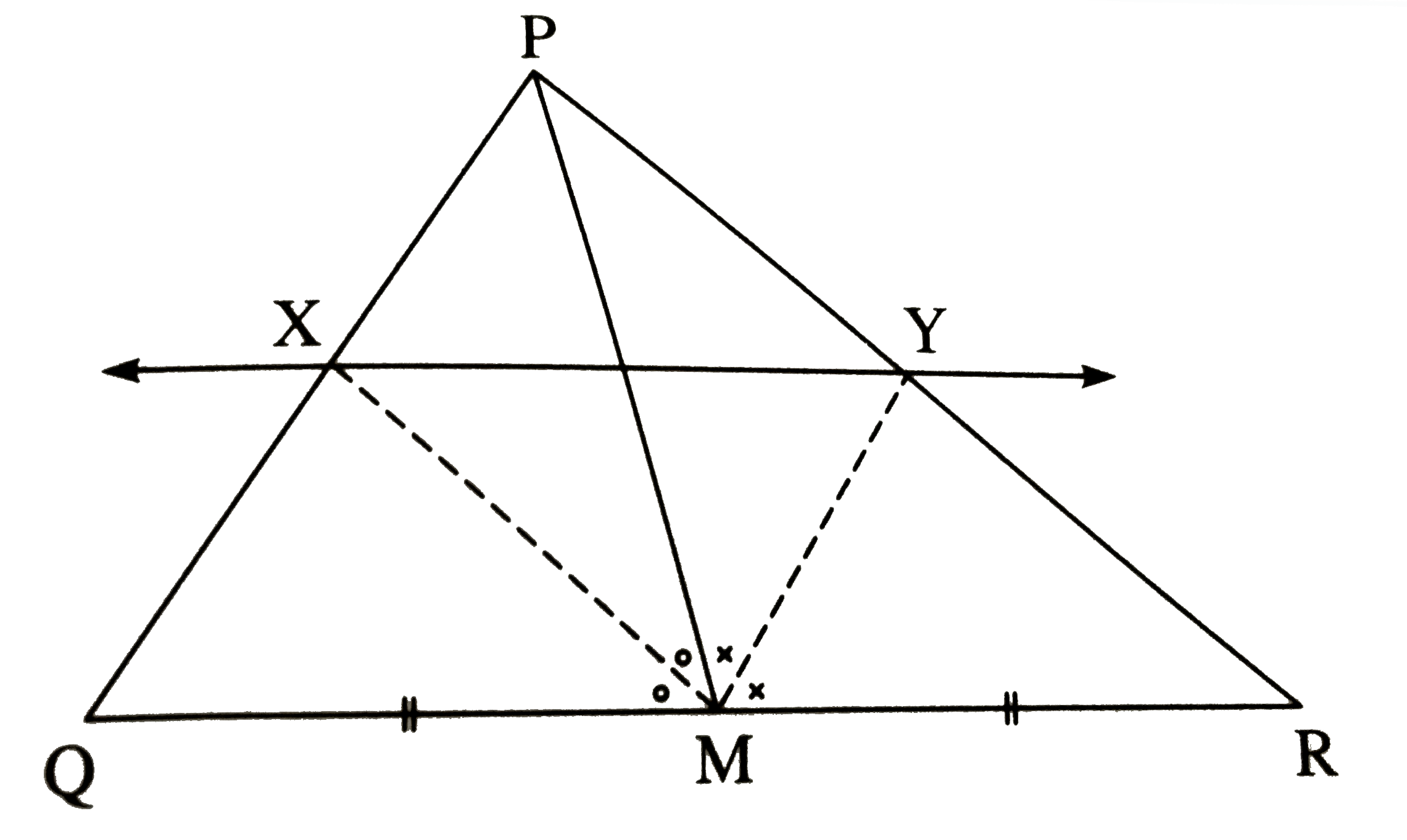
In `DeltaPQR` seg PM is a median. Angle bisectors of `/_PMQ` and `/_PMR` interesect `side PQ` and `side PR` in points `X` and `Y` respectively. Prove that `XY||QR`.
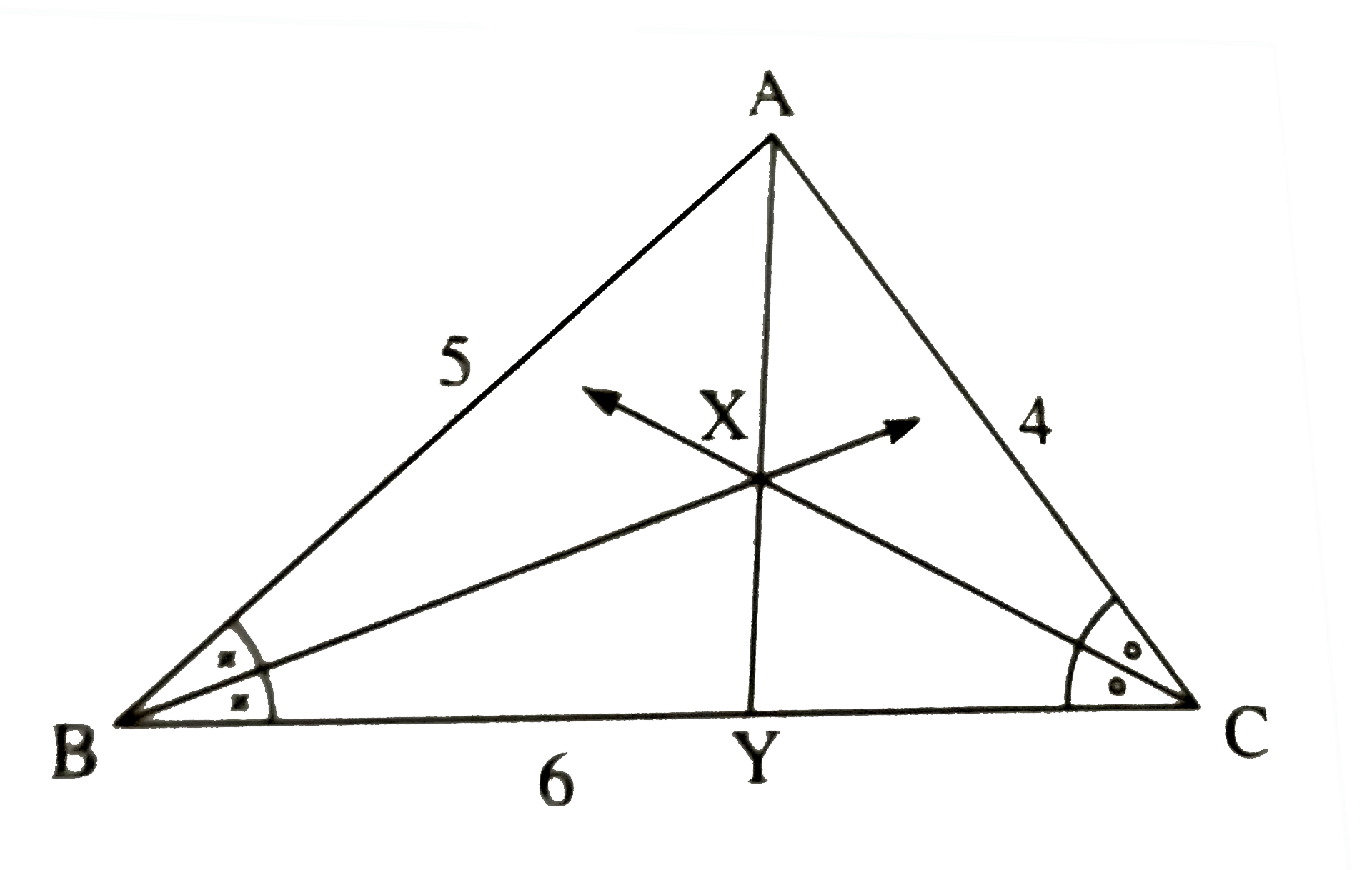
View SolutionIn the figure bisectors of `/_B` and `/_C` of `DeltaABC` intersect each
other in point X. Line AX intersects side BC in pont Y. `AB=5, AC=4, BC=6` then find `(AX)/(XY)`
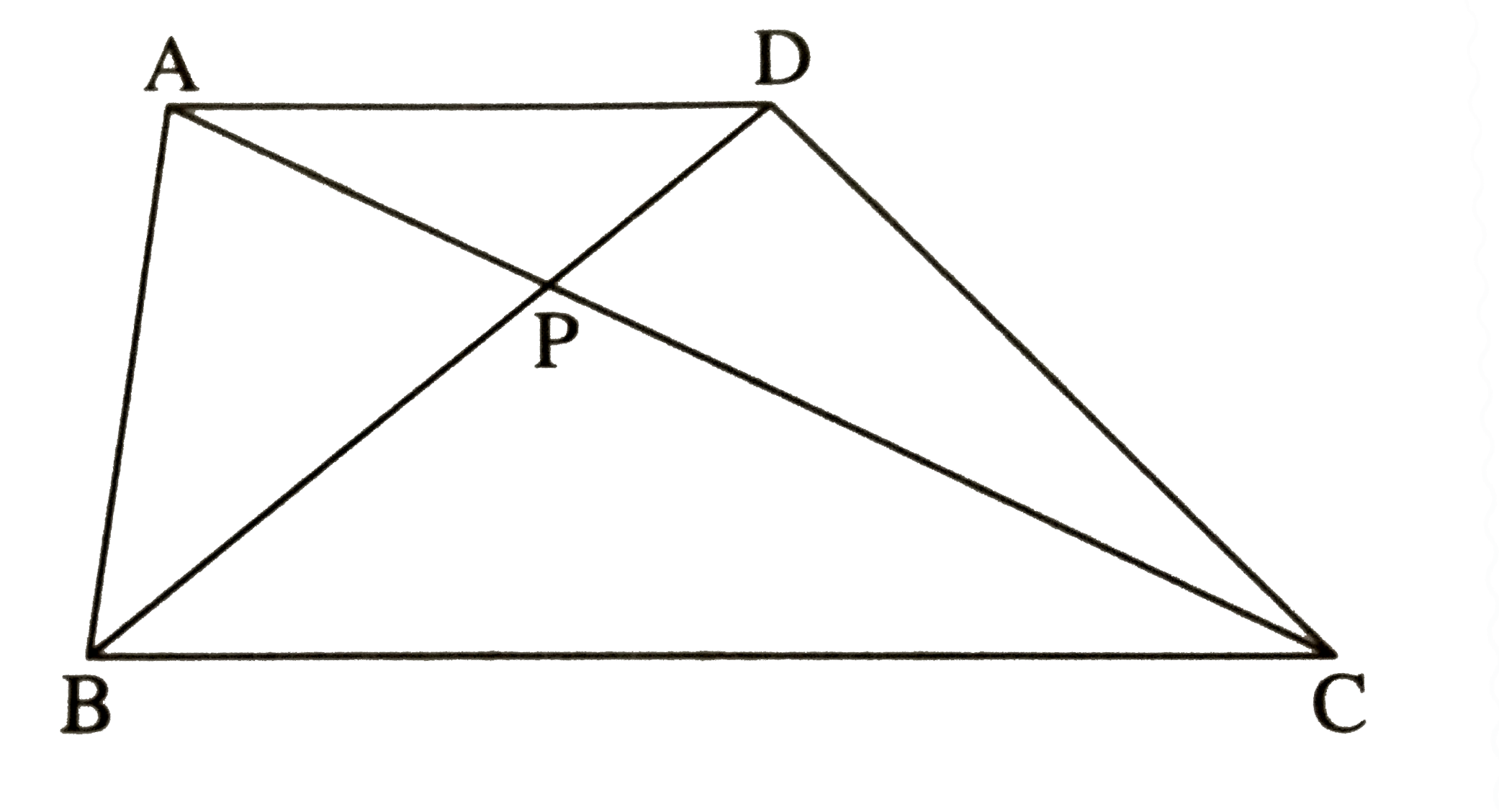
View SolutionIn `square ABCD`, seg `AD||` seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that `(AP)/(PD)=(PC)/(BP)`.
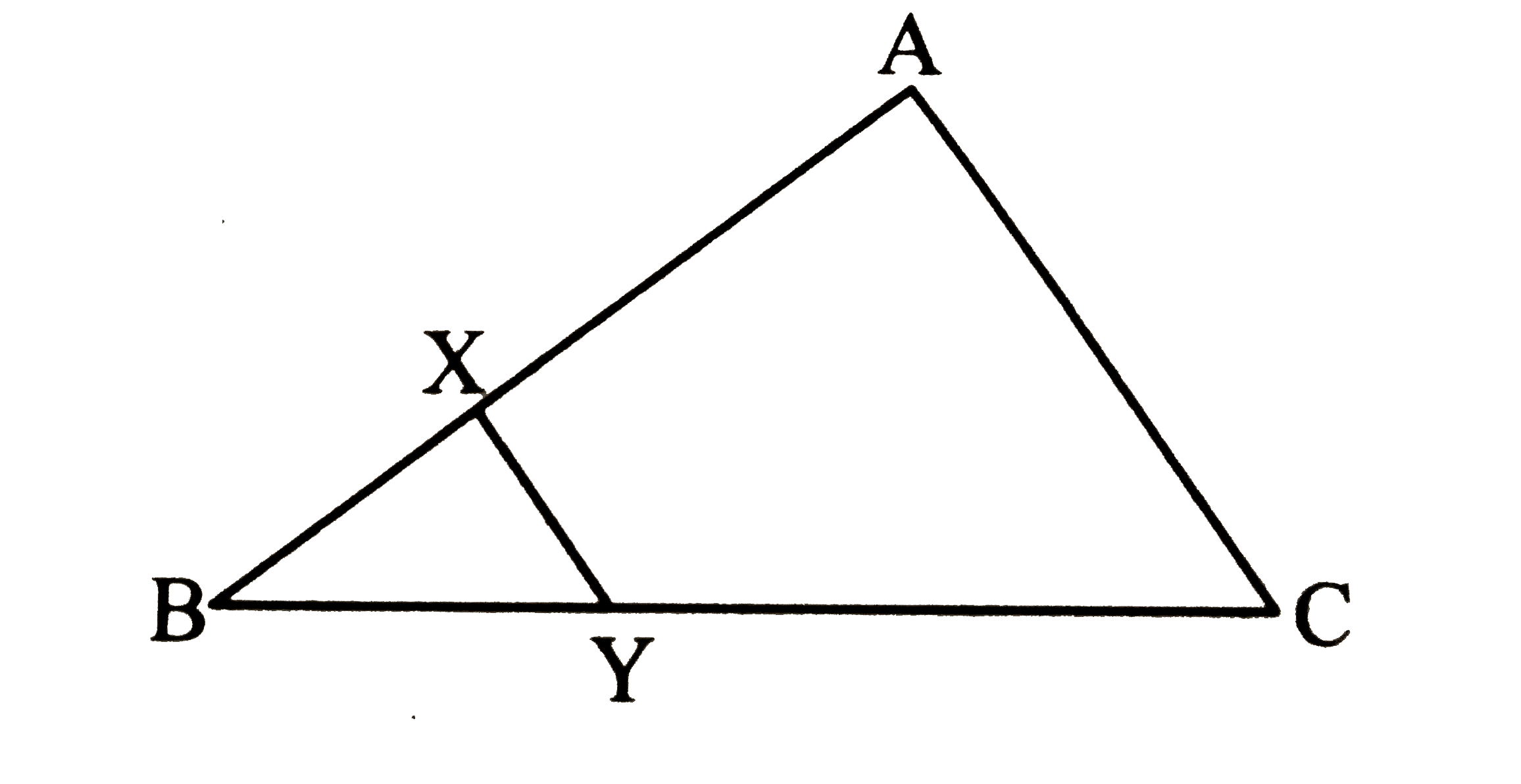
View SolutionIn the adoining figure, XY `abs()` seg AC. If 2 AX = 3 BX and XY = 9, find the value of AC.
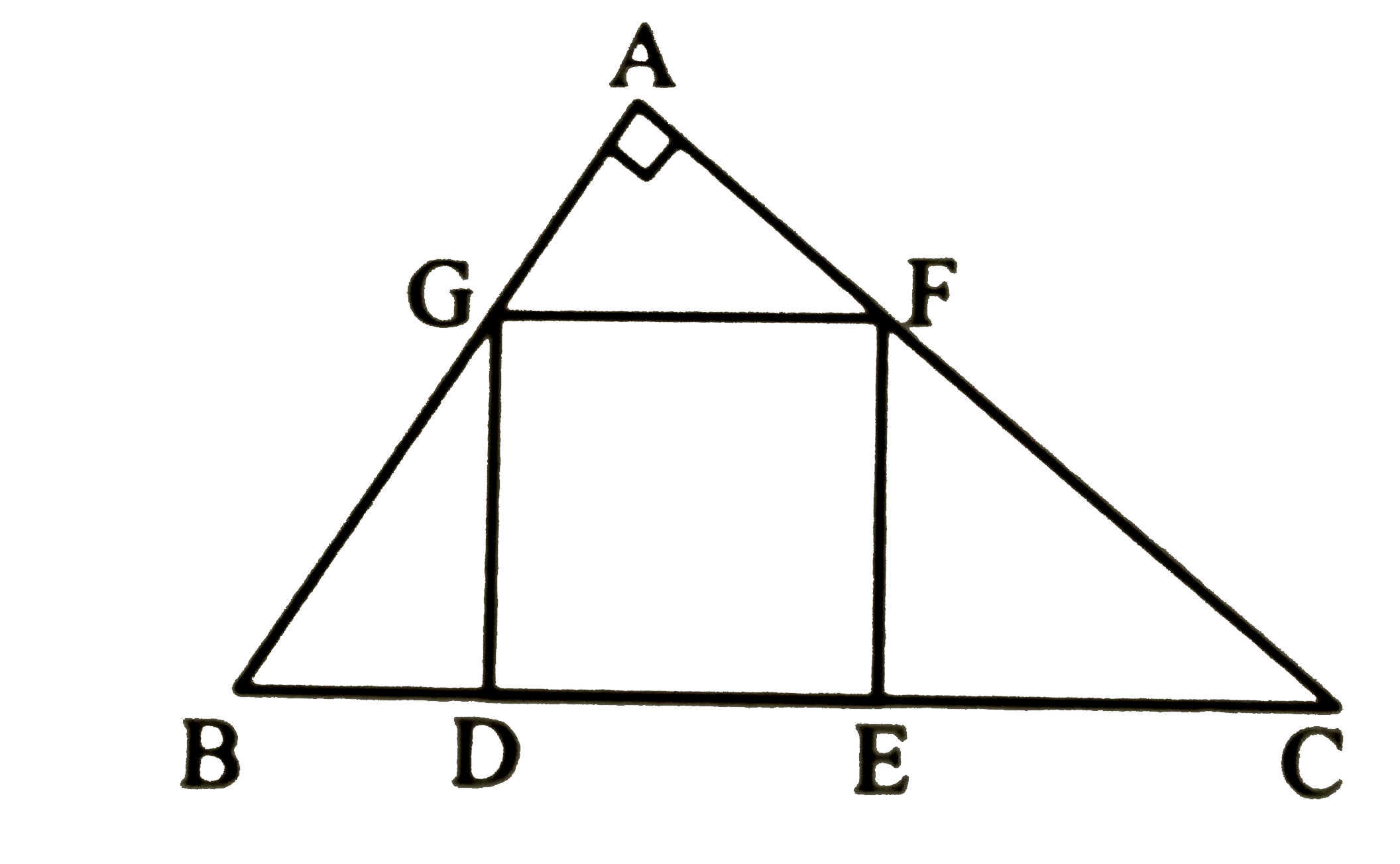
View SolutionIn the adjoining figure, the vertices of square DEFG are on the sides of `DeltaABC`. If `angleA = 90^@`, then prove that `DE^2 = BD xx EC`.
View Solution
Problem Set - 1 questions and complete solutions for chapter SIMILARITY of TARGET PUBLICATION of Class 10
All Exercises from TARGET PUBLICATION Class 10 MATHS SIMILARITY
- Activites for Practice
- Additonal Problems for Practice( Basid on Practice Set 1.1)
- Additonal Problems for Practice(Based on Practice Set 1.2)
- Additonal Problems for Practice(Based on Practice Set 1.3)
- Additonal Problems for Practice(Based on Practice Set 1.4)
- Chapter Assessment
- Fill in the properly. State the reason.
- Multiple Choice Questions
- Practice Set 1.1
- Practice Set 1.2
- Practice Set 1.3
- Practice Set 1.4
- Problem Set - 1
- Textual Activity