Complete Solutions to Chapter Assessment of chapter CIRCLE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLE |
| TARGET PUBLICATION | Chapter Assessment |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
If two circles with diameter 8cm and 6 cm touch externally,
then the distance between their centres is ______.
View SolutionIn the given figure , O is the centre of the circle. If m(arc AXB)=`80^@`,
then `mangleAOB`=

View SolutionIn the given figure ,secants AP and CP intersect in point P. If AP=12,PB=5,CP=20, then DP=
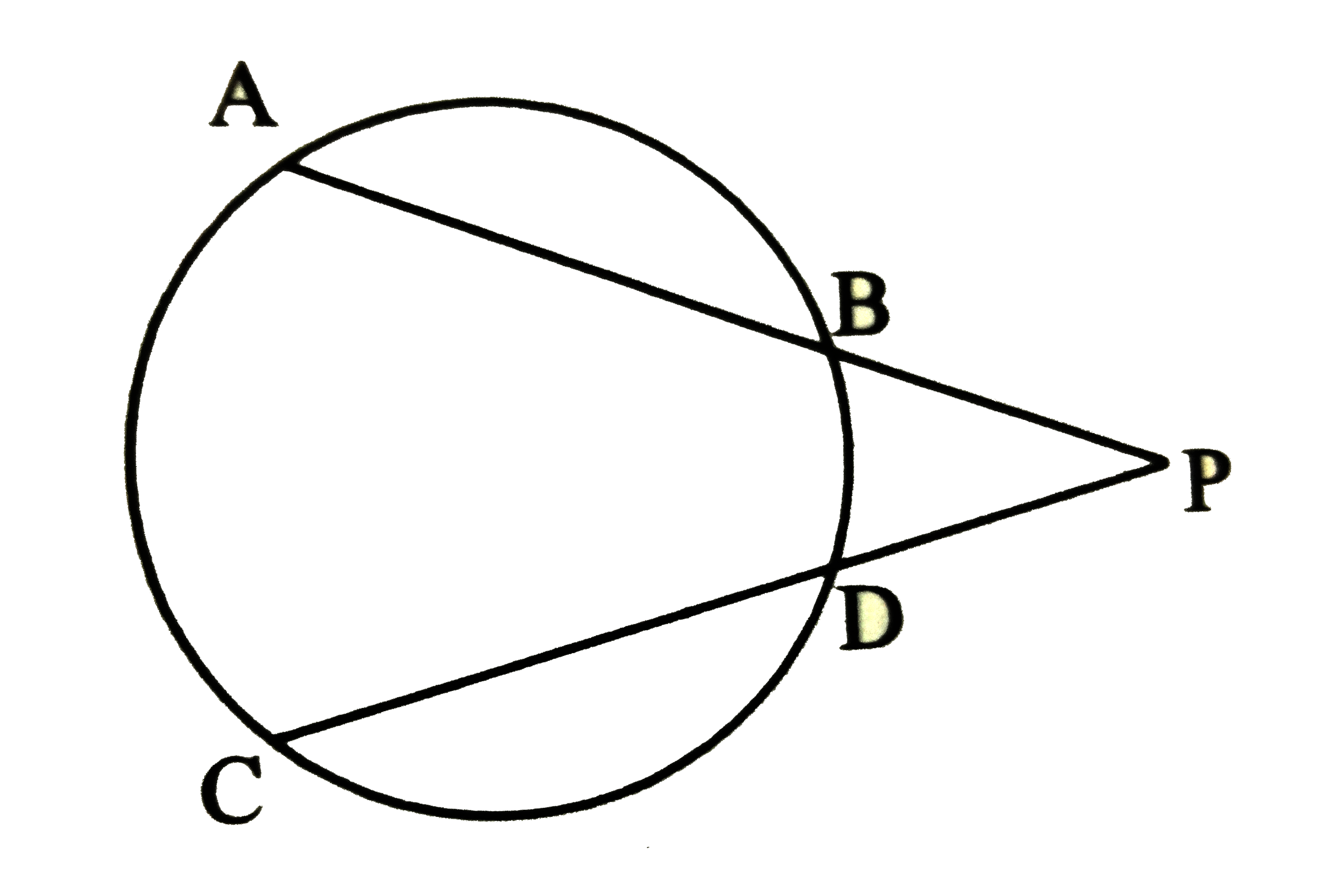
View SolutionIn the given figure , if line BC is tangent and `angleBAD=50^@`, then `mangleDBC`=
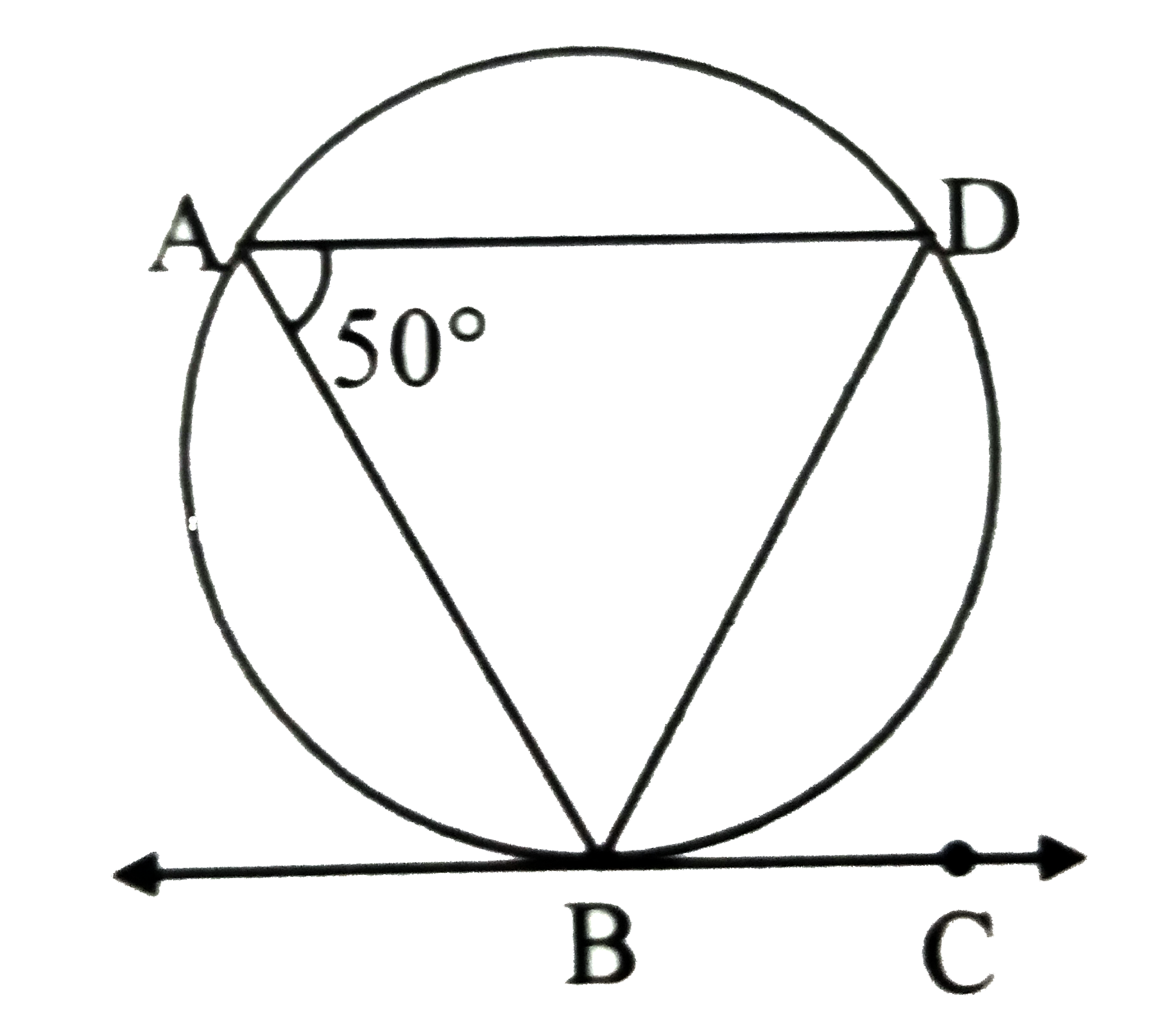
View SolutionIn the figure, point A is the centre of the circle and its tangent CD touches the circle at point B, The radius of the circle is 4cm .If `mangleBAC=30^@`, then find AC
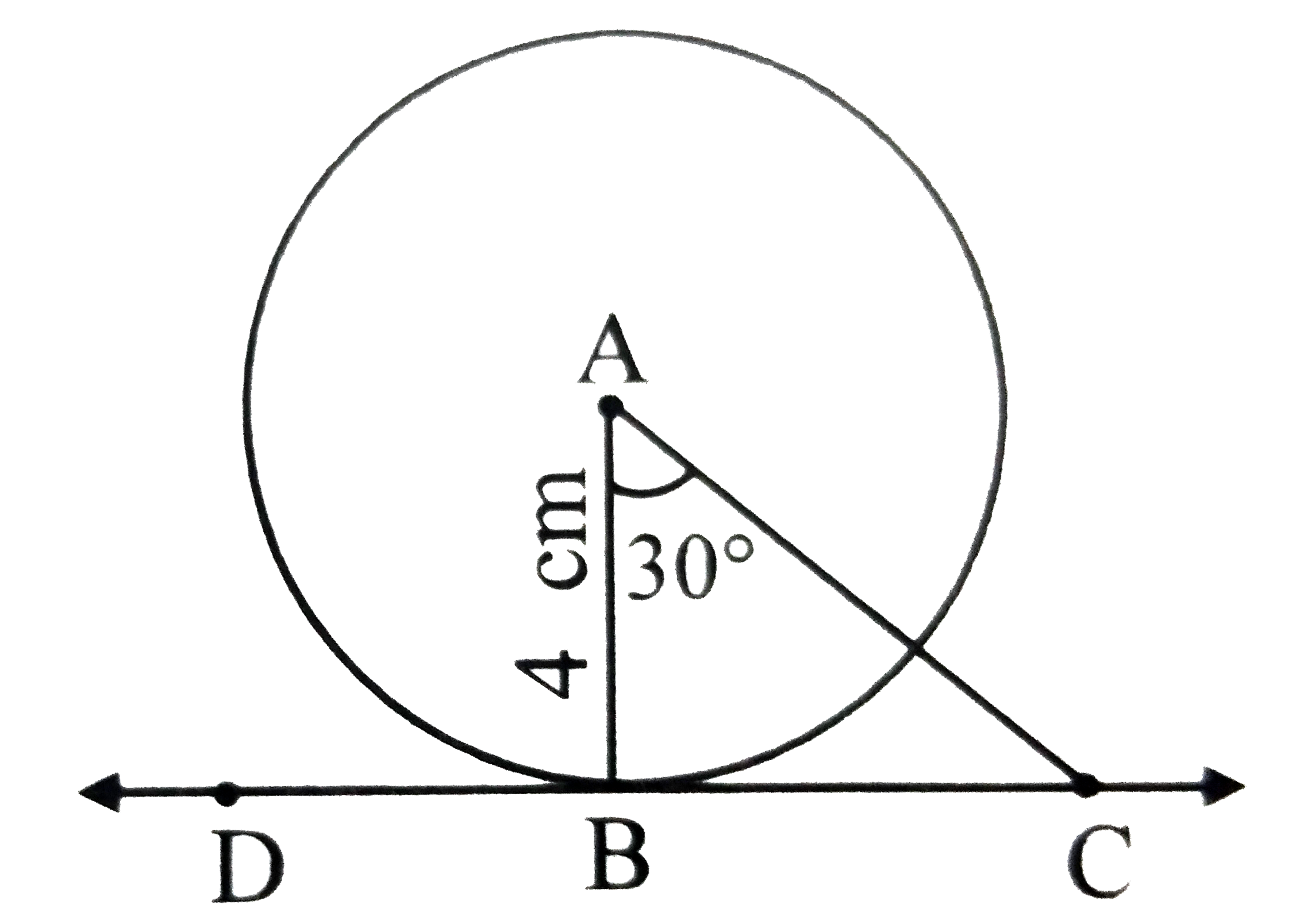
View SolutionFind the radius of the circle passing through the vertices of a right angled traingle the lengths of whose perpendicular sides are 8
and 15.
View SolutionIn the adjoining figure ,two circles intersect at points M and N. |
Secants drawn through M and N intersect the circles at points R,S
and P,Q respectively. Prove that: seg SQ`||`seg RP.
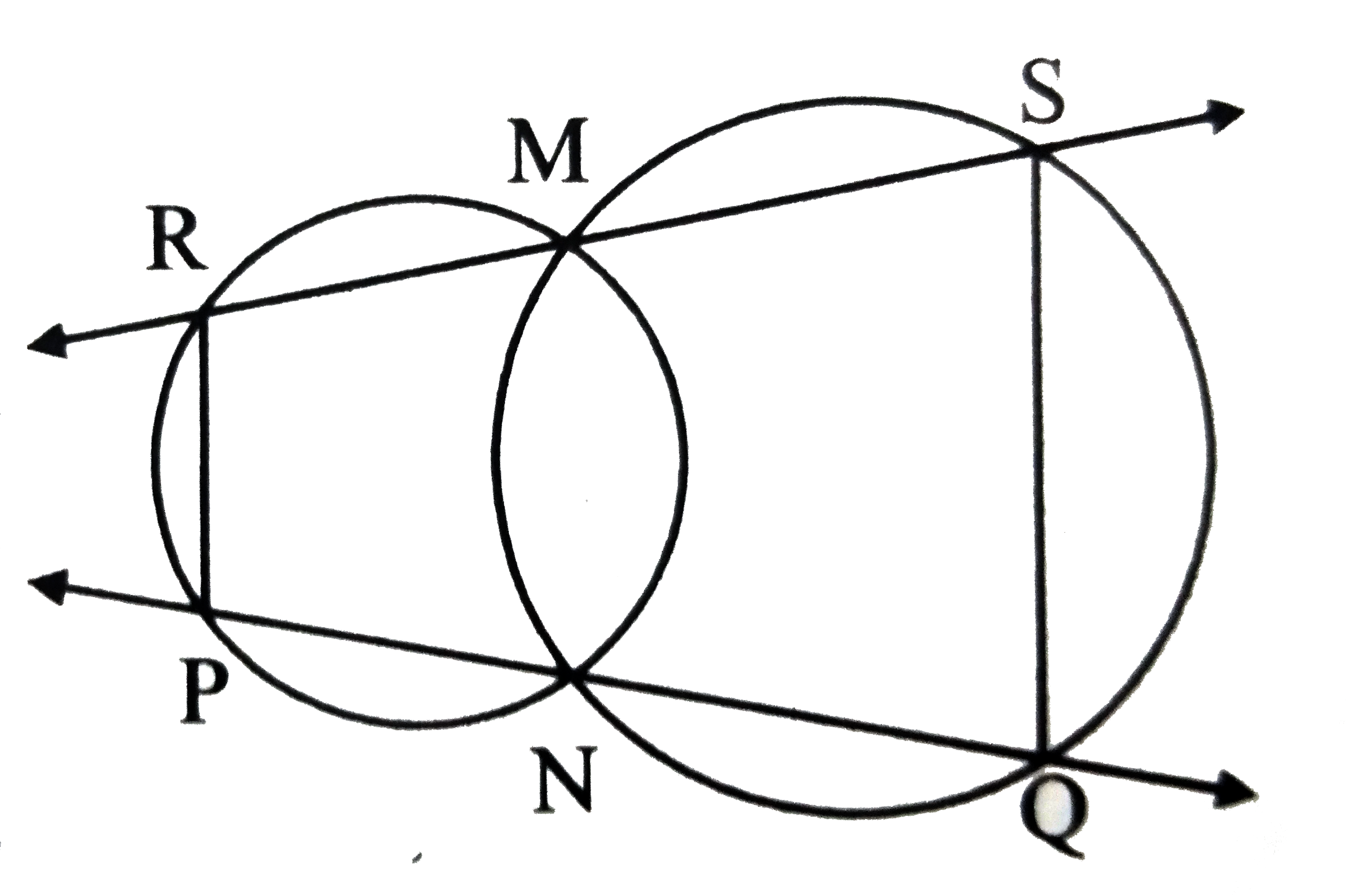
View SolutionIn the following figure, a tangent segment PA touching a circle
in A and a secant PBC are shown. If AP=12,BP=9, find BC.
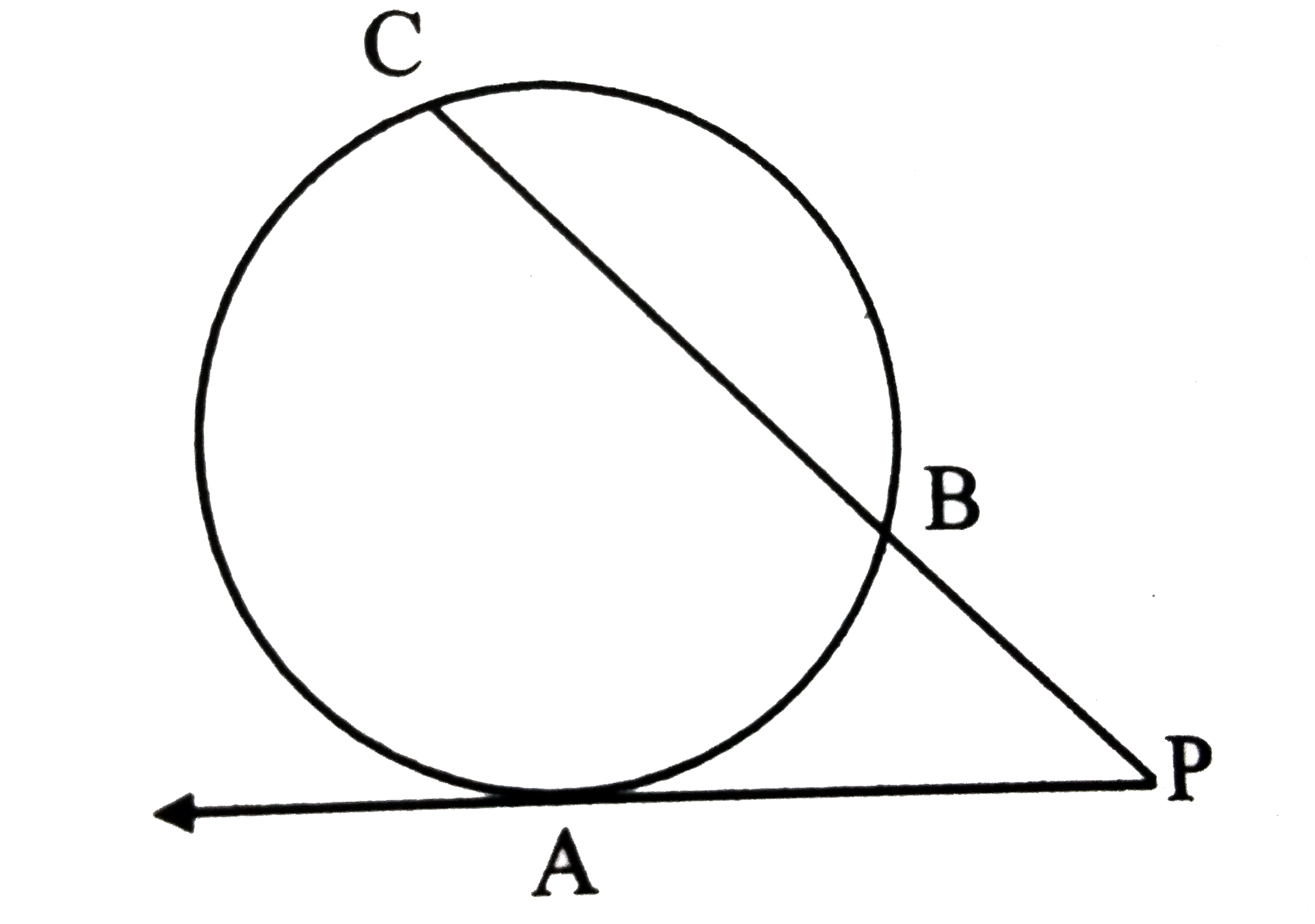
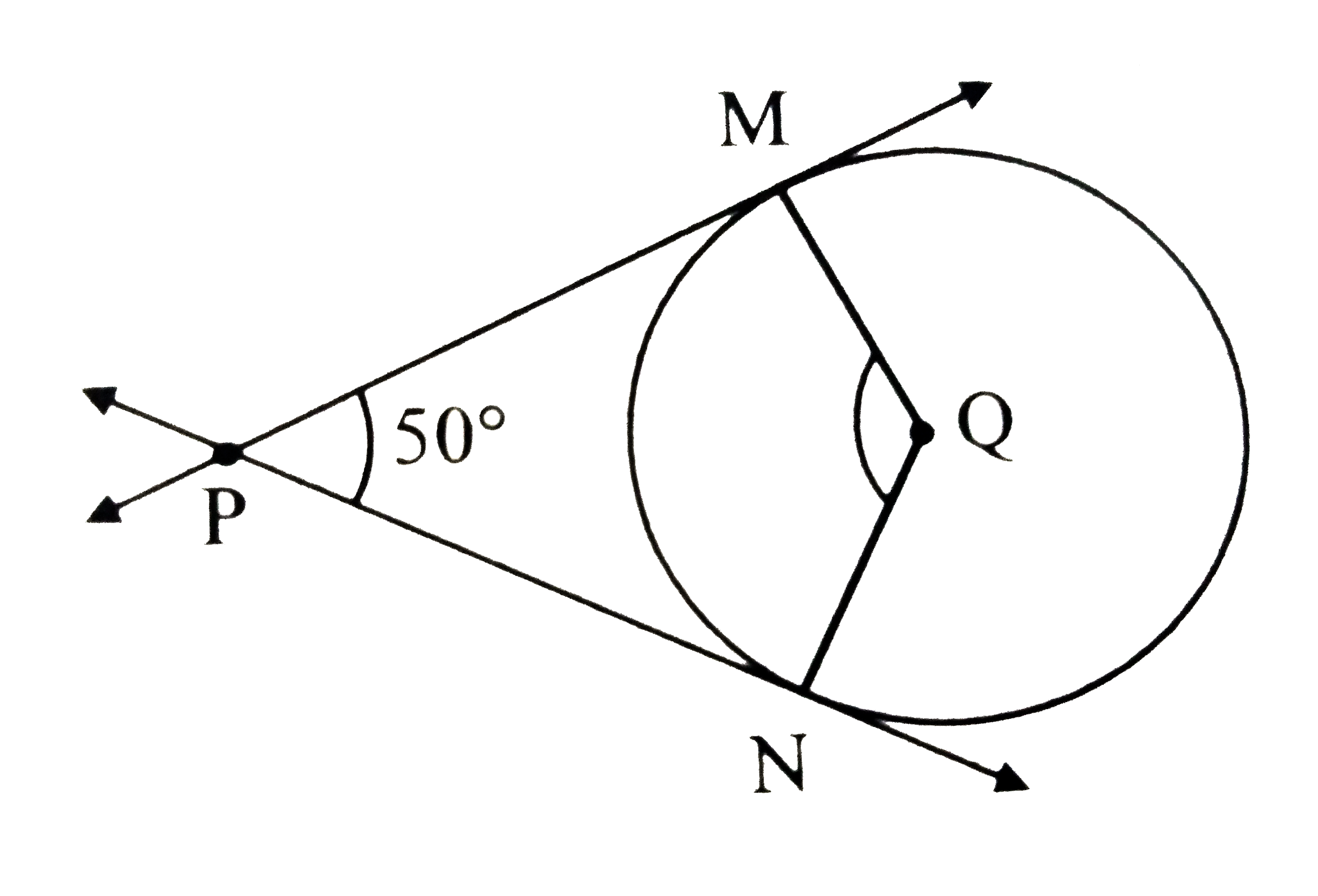
View SolutionIn the given figure, Q is the centre of the circle and PM ,PN are
tangent segments to the circle. If `angleMPN=50^@` find `angleMQN`.
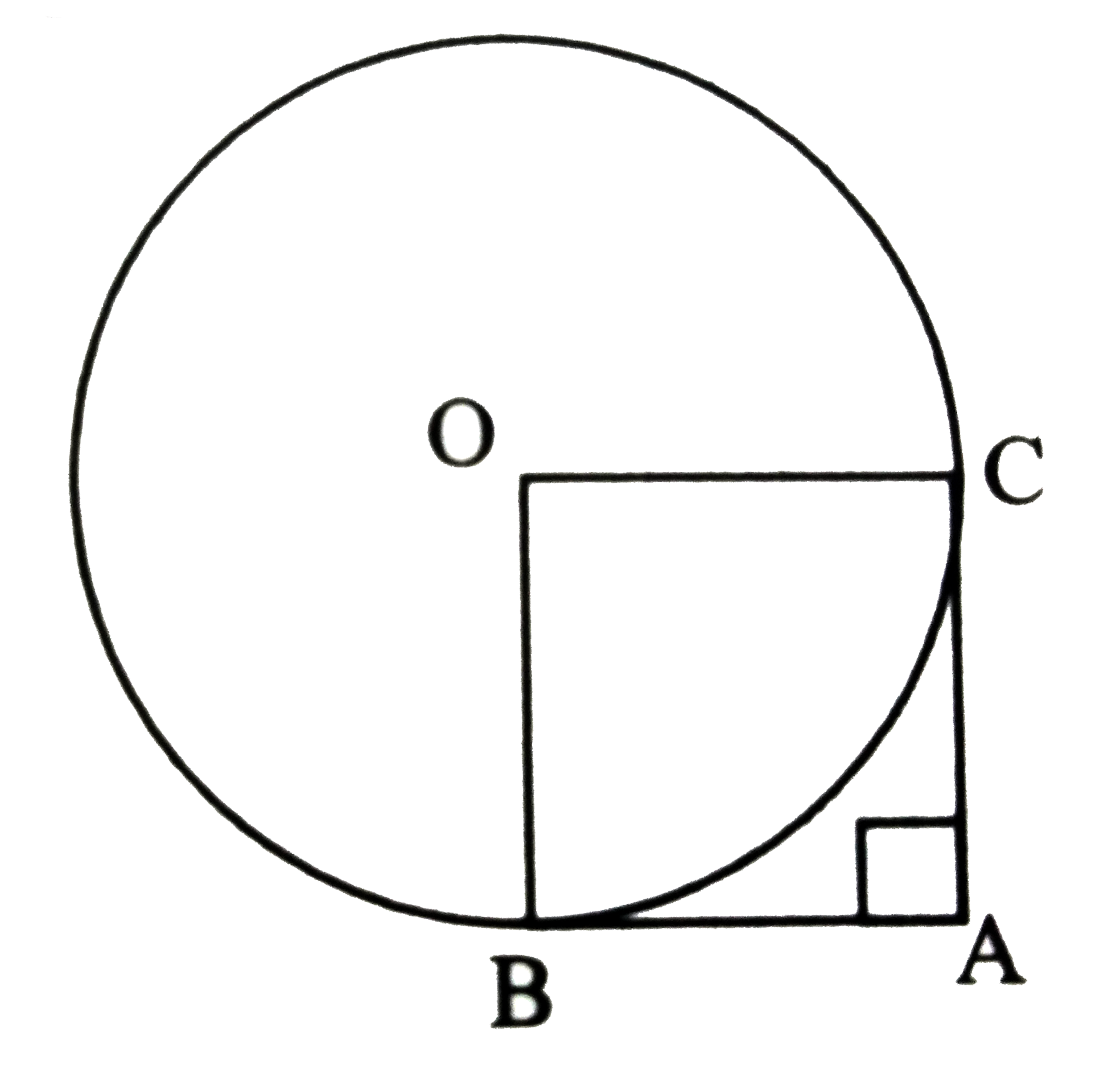
View SolutionIn the given figure , O is the centre of the circle. AB and AC are
tangents to the circle such that BA`bot`CA.
Prove that `square` BACO is a square.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionProve that the opposite sides of a quadrilateral circumscribing a
circle subtend supplementary angles at the centres of the circle.
View SolutionIf two equal chords of a circle intersect within the circle, prove that
the segments of one chord are equal to corresponding segments
of the other chord.
View SolutionProve that, "If chords of congruent circles subtend equal angles at their centre, then the chords are equal."
View Solution
Chapter Assessment questions and complete solutions for chapter CIRCLE of TARGET PUBLICATION of Class 10