Complete Solutions to Problem Set-3 of chapter CIRCLE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLE |
| TARGET PUBLICATION | Problem Set-3 |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other.What is the distance between their centres?
View SolutionTwo circles intersect each other such that each circles pass through the centre of the other.If the distance between their centres is 12,what is the radius of each circle?
View SolutionA circle touches all sides of a parallelogram.so the parallelogram must be a ……
View SolutionLength of a tangent segment drawn from a point which is at
a distnace 12.5 cm from the centre of a circle is 12cm , find the diameter of the circle.
View SolutionIf two circles are touching externally,how many common tangents of them can be drawn?
View Solution`/_ACB` is inscribed in arc ACB of a circle with centre O.If `/_ACB=65^@`,find m(arc ACB)
View SolutionChords AB and CD of a circle intersect inside the circle at point E. If AE=5.6, EB=10, CE=8, find ED. a)7 b)8 c)11.2 d)9
View SolutionIn a cyclic `square ABCD`, twice the measure of `/_A` is thrice the measure of `/_C`. Find the measure of `/_C` a)`36^@` b)`72^@` c)`90^@` d)`108^@`
View SolutionPoints A,B,C are on circle, such that `m(arc AB)=m(arc BC)=120^@`. No point, except point B, is common to the arcs. What is the type of `triangle ABC`? a)Equilateral triangle b)Scalene triangle c)Right angled triangle d)Isosceles triangle
View SolutionSeg XZ is a diameter of a circle. Point Y lies in its interor. How many
of the followint statements are true?
(1) It is a not possible that `/_XYZ` is an acute angle.
(2) `/_XYZ` can't be a right angle
(3) `/_XYZ` is an obtuse angle.
(4) Can't make a dfinite statement for measure of ` /_XYZ`
View SolutionIn the adjoining figure, O is the centre of the circle. Seg AB, seg AC
are tangent segments. Radius of the circle is r and l(AB) = r.
Prove that , `square` ABOC is a square.
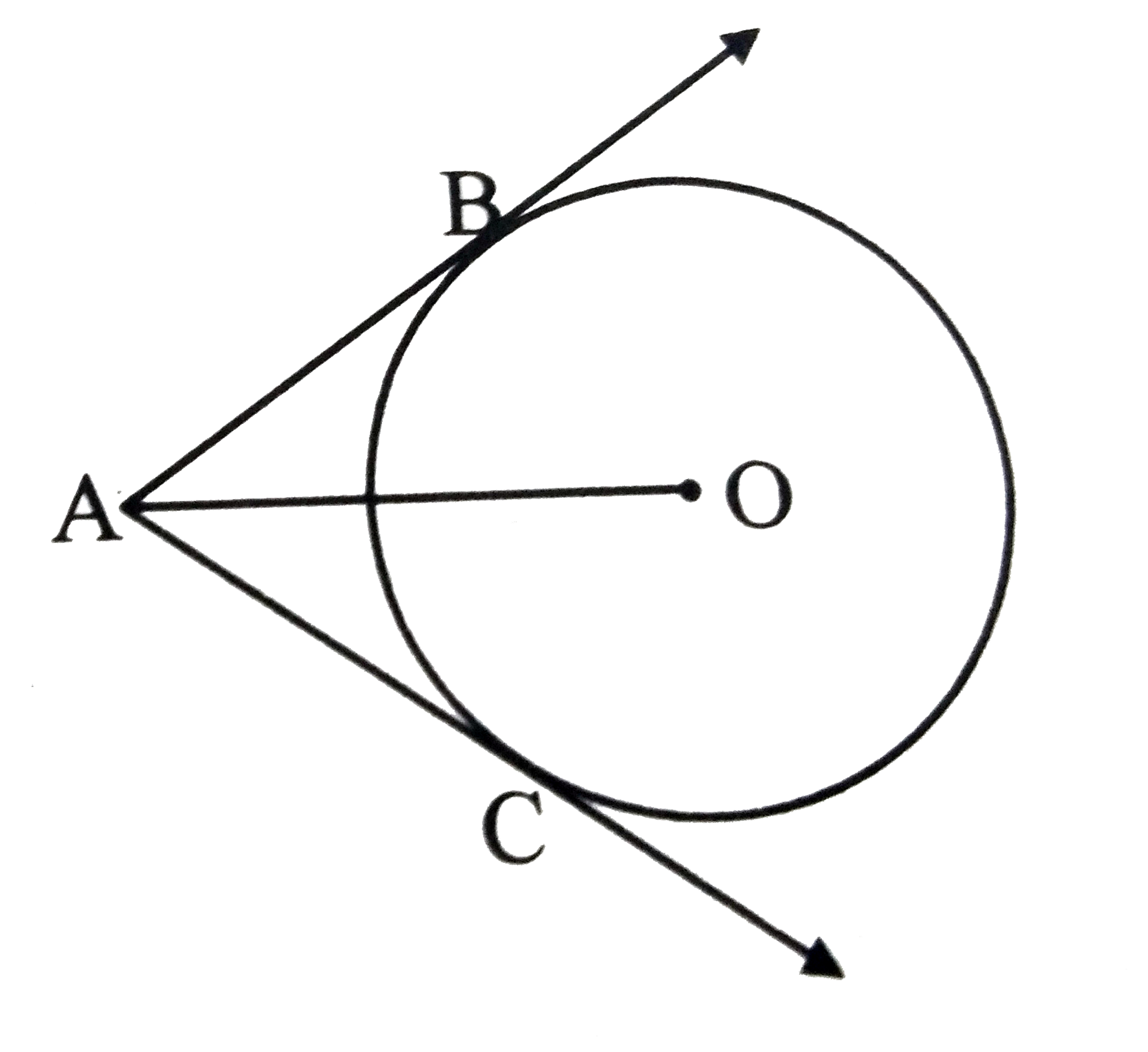
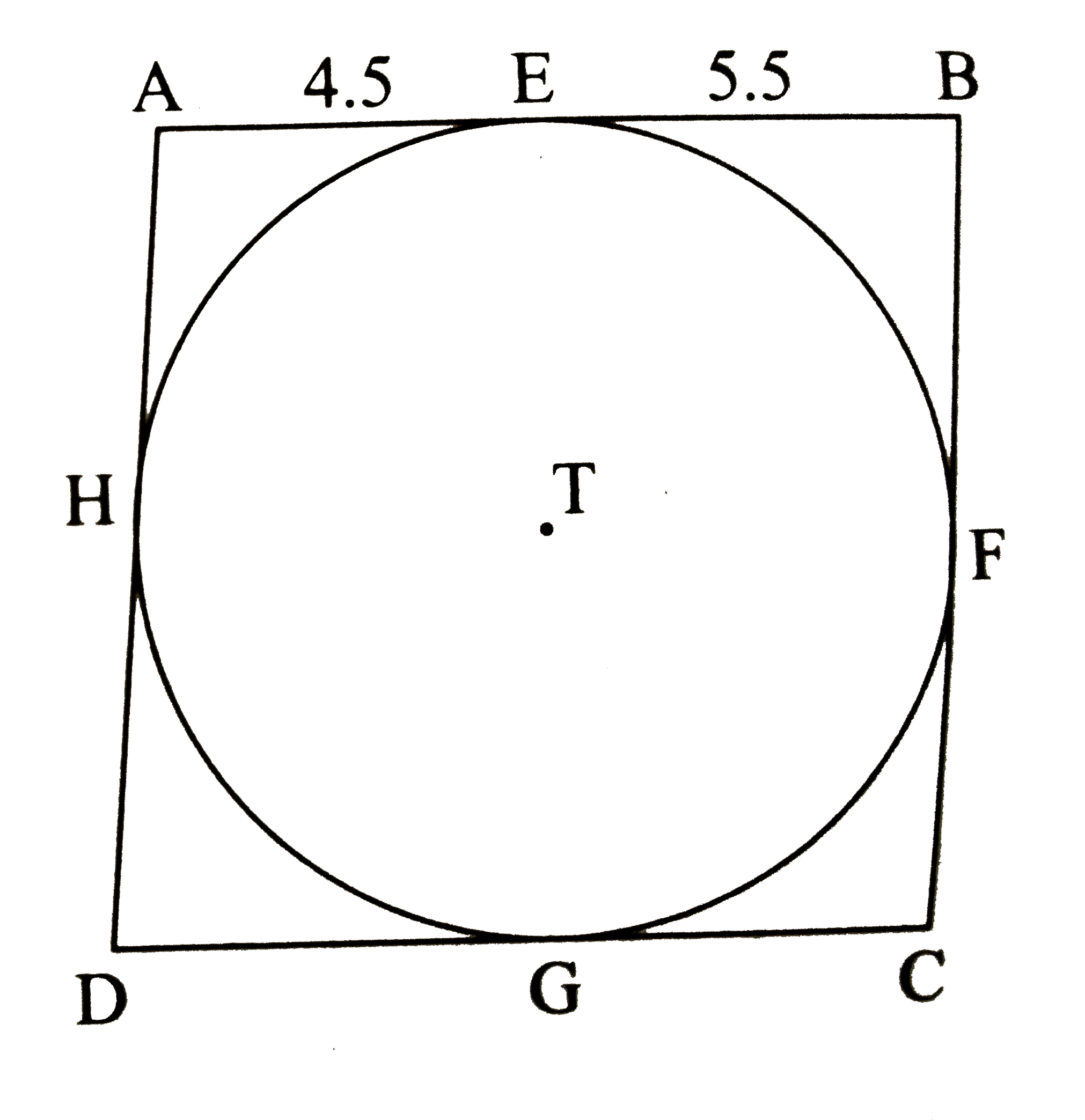
View SolutionIn the figure, `square ABCD` is a parallalogram. It circumscribes the
cirlcle with centre T. Point E,F,G,H are touching points. If AE = 4.5,
EB = 5.5, find AD.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and
the other circle at B and D. Prove the AC|| BD
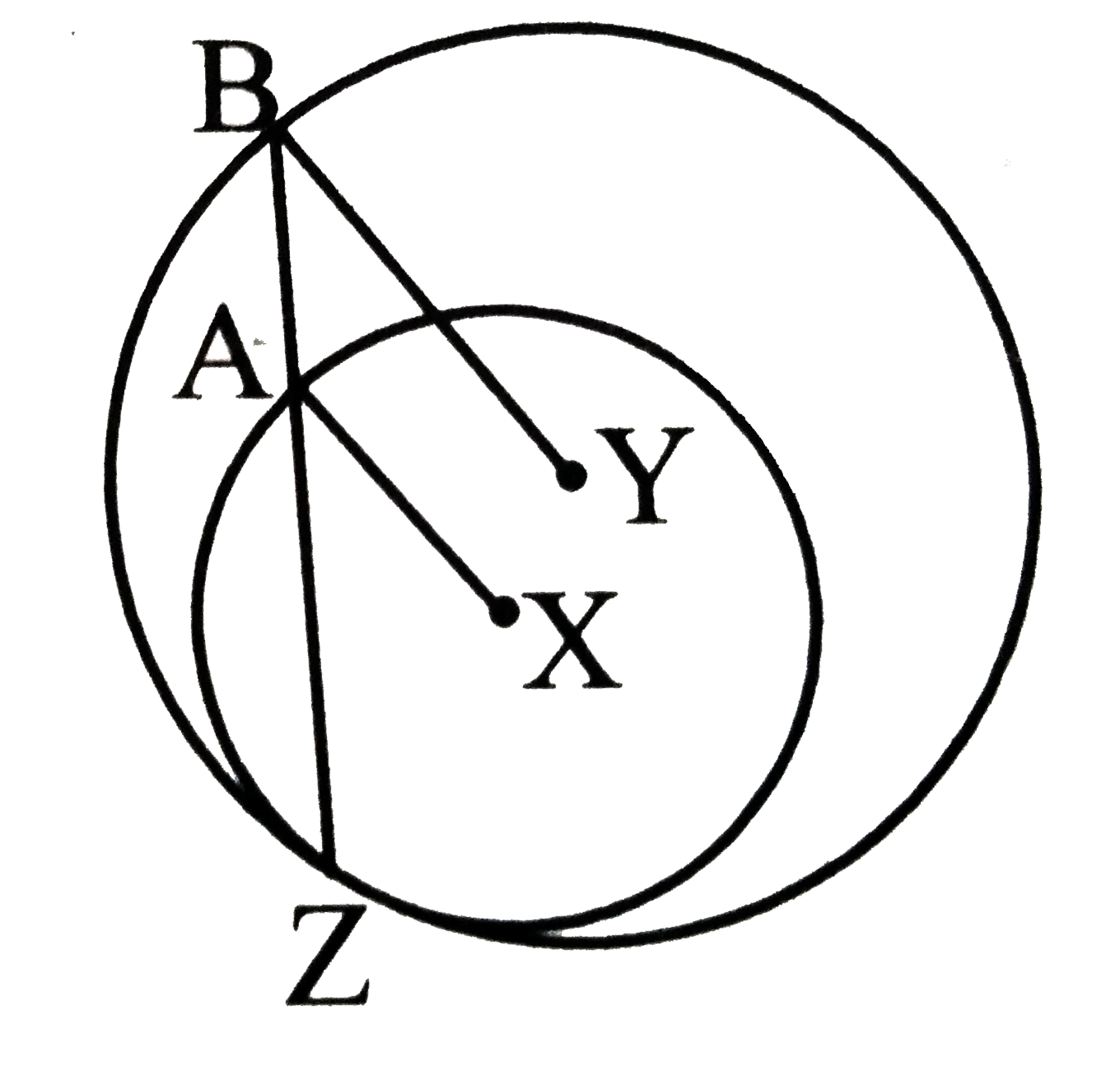
View SolutionIn the adjoining figure, circles with centres X and Y touch internally
at point Z. Seg BZ is a chord of bigger circle and it intersects smallest
circle at point A. prove that, seg AX `||`seg BY.
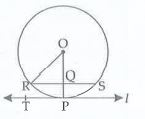
View SolutionIn the adjoining figure,line l touches the circle at P.O is the centre.Q is the mid point of radius OP.Chord `RS||line l`RS=12,find radius of the circle.
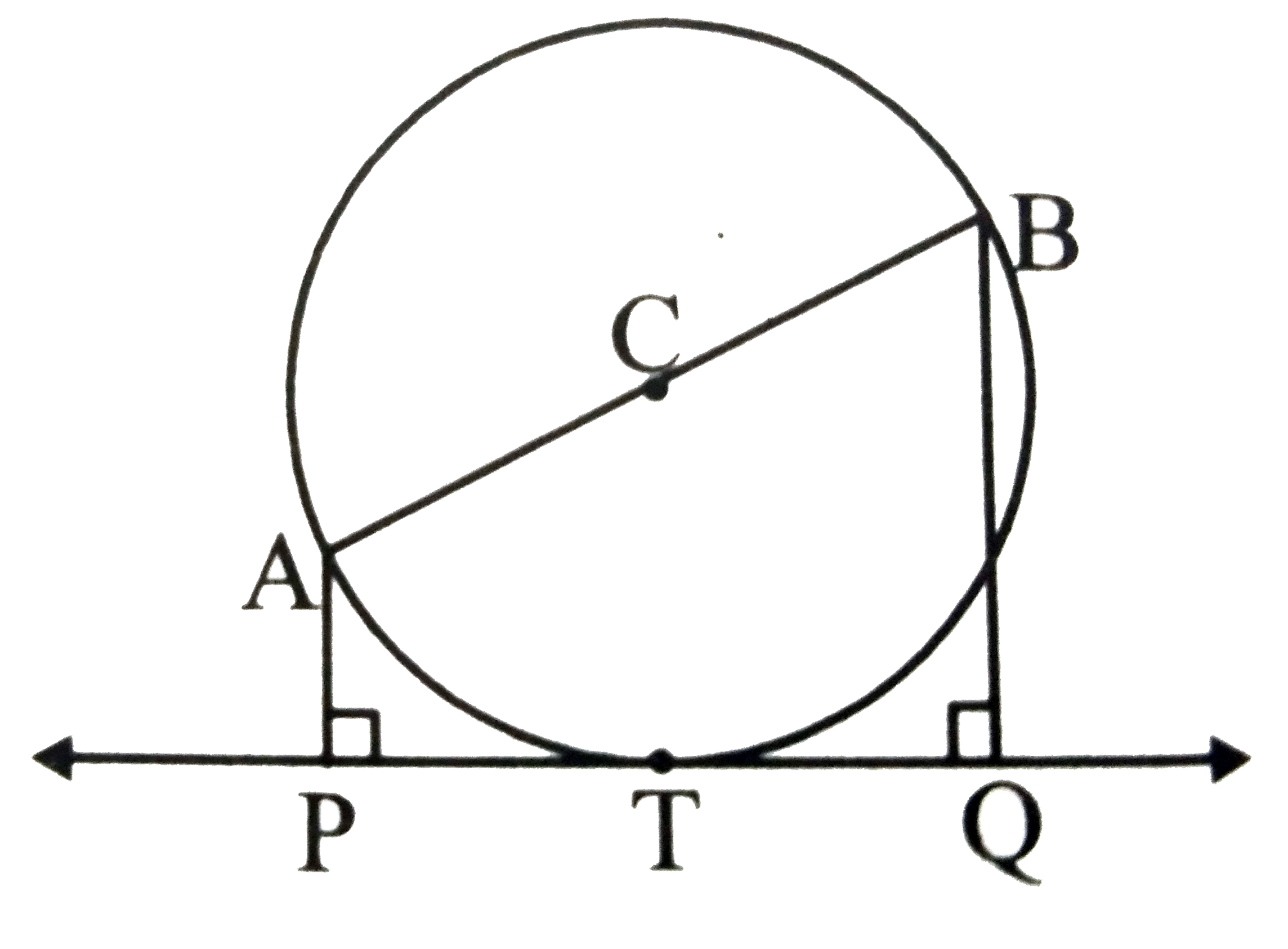
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre C.
Line PQ is a tangent, which touches the circle at point T.
Seg AP`bot` line PQ and seg BQ`bot`line PQ.
Prove that seg CP`cong`seg CQ.
View SolutionProve that any three points on a circle cannot be collinear.
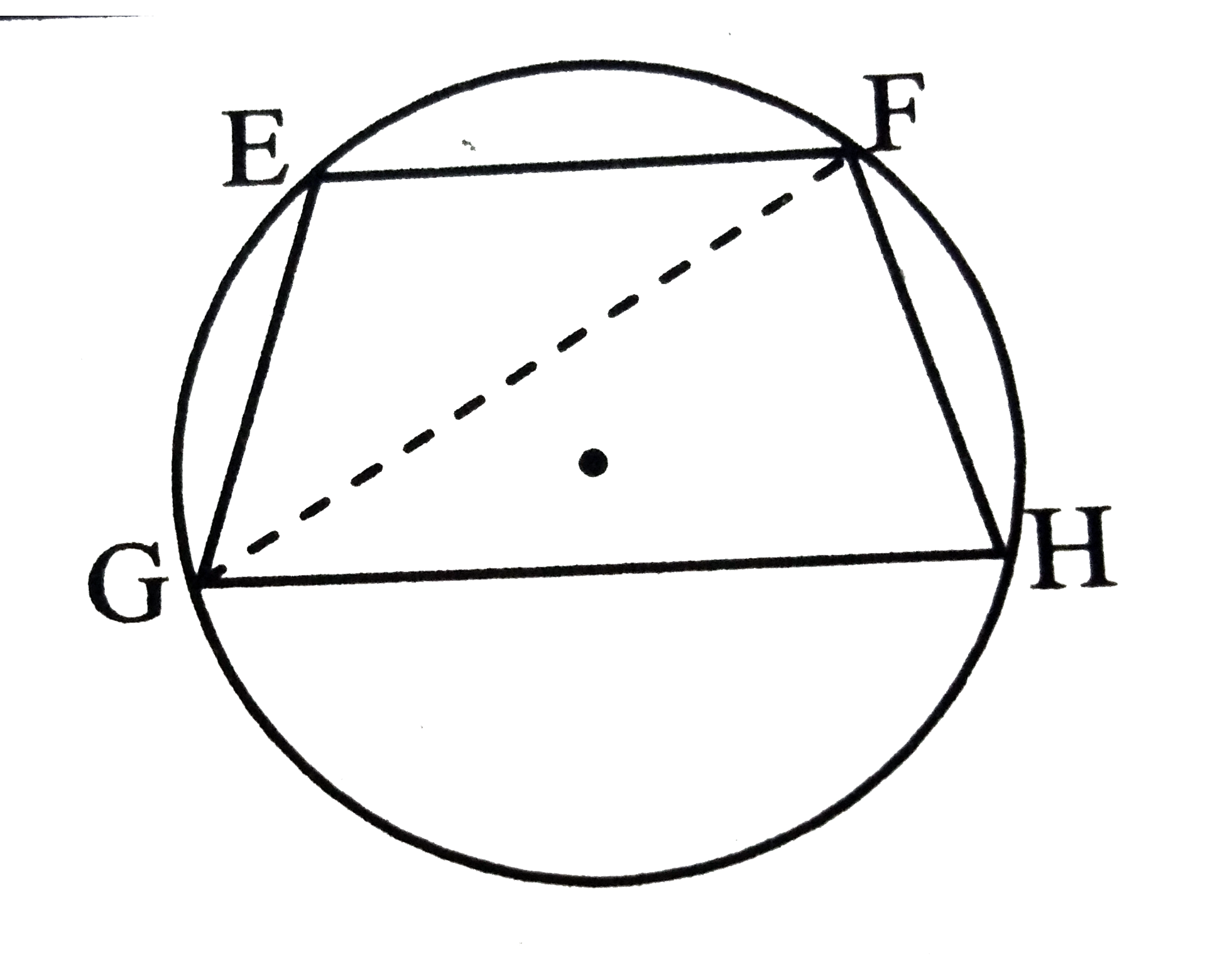
View SolutionIn the adjoining figure ,chord EF `||` chord GH.
Prove that, chord EG`cong`chord FH.
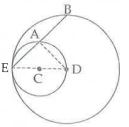
View SolutionA circle with centre C touches the circle with centre D internally in the point E. Point D lies on the smaller circle. Chord EB of the external circle intersects internal circle at point A. Prove that `seg EA~=seg AB`
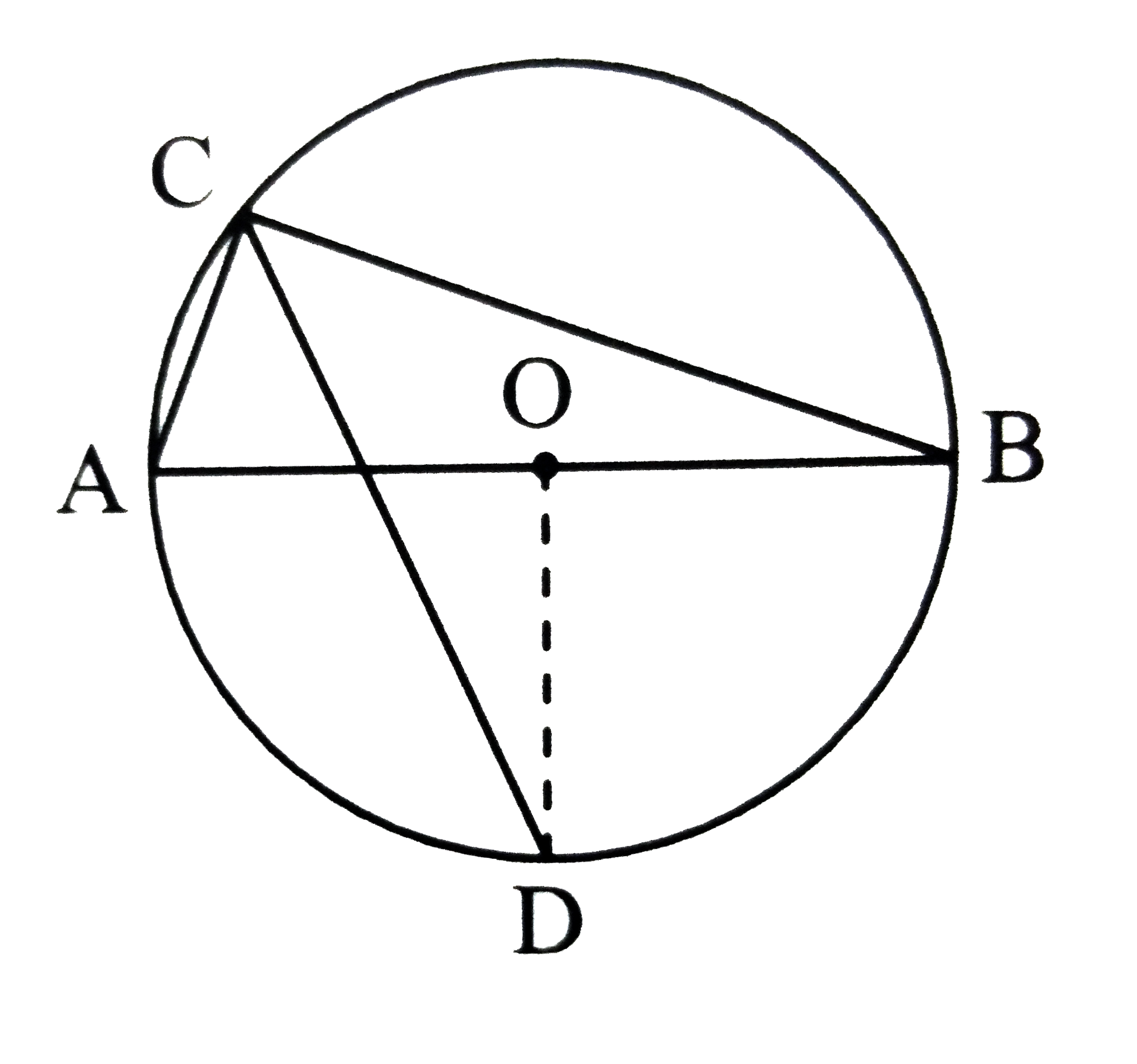
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of `angleACB` intersects the circle at point D.
Prove that ,seg `ADcongseg BD`.
View SolutionIn the adjoining figure, two circles intersect each other at point M and N. Secants drawn from point M and N intersect cirlces at point R, S, P and Q as shown in the figure. Prove that seg PR || seg QS
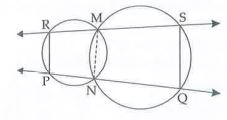
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and
the other circle at B and D. Prove the AC|| BD
View SolutionIn the adjoining figure, seg AD `bot` side BC, seg BE `bot `side AC,
seg CF`bot` side AB. Point O is the orthocentre.
Prove that , point O is the incentre of `DeltaDEF`.
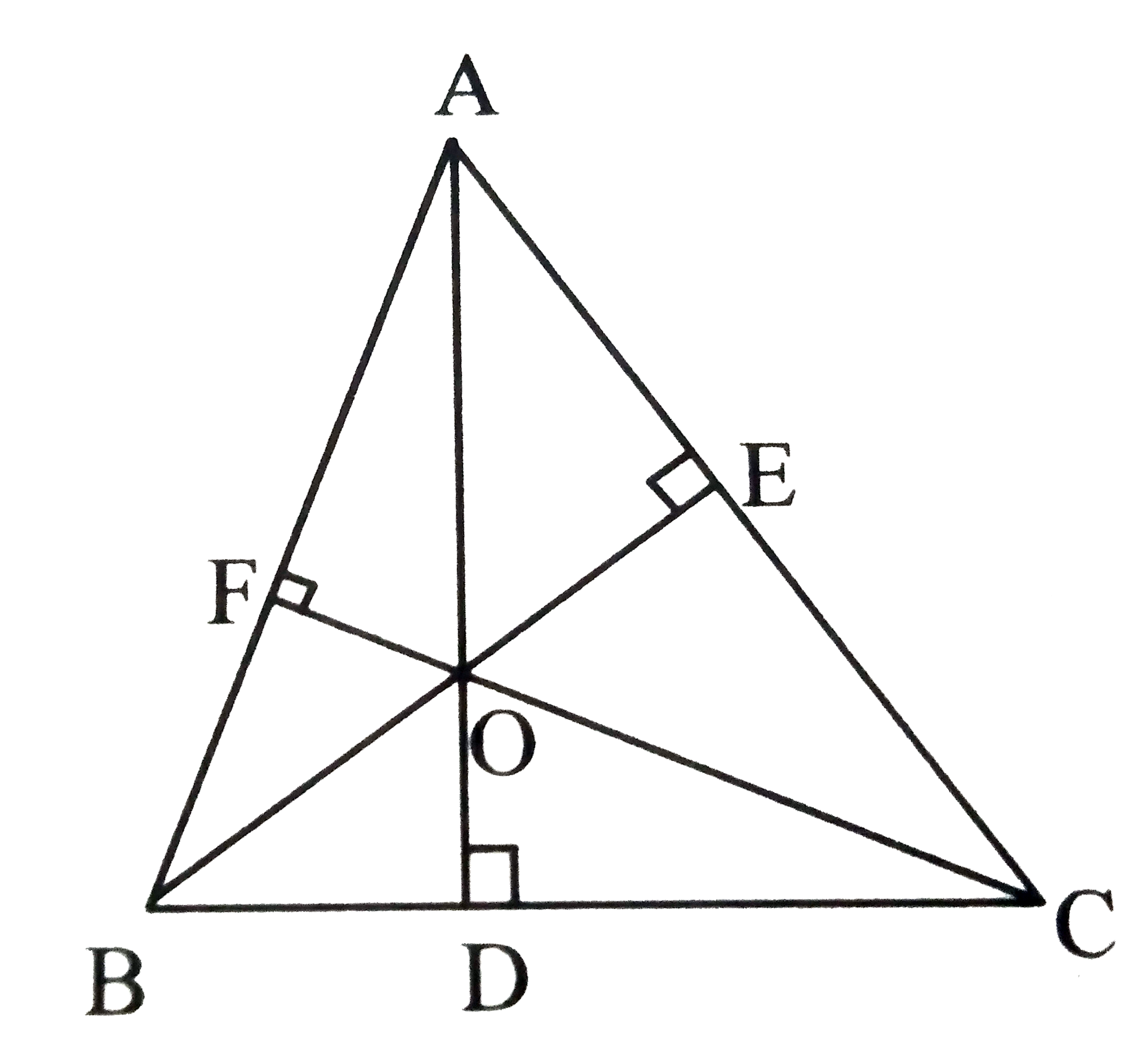
View Solution
Problem Set-3 questions and complete solutions for chapter CIRCLE of TARGET PUBLICATION of Class 10