Complete Solutions to QUESTION BANK of chapter COORDINATES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | COORDINATES |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Find the following:
i) The y coordinate of any point on the 'x' axis.
ii) The 'x' coordinate of any point on the 'y' axis.
iii) The coordinates of the origin.
iv) The y coordinate of any point on the line through (0,1), parallel to the 'x' axis.
v) The x coordinate of any point on the line through (1,0), parallel to the 'y' axis.
View SolutionFind the coordinates of the other three vertices of the rectangle below:
'(##VPU_TTT_MAT_X_P01_C06_E01_002_Q01##)'
View SolutionIn the rectangle shown below,the sides are parallel to the axes and origin is the mid point:What are the coordinates of the other three ertices?

View SolutionThe triangle shown below is equilateral:
'(##VPU_TTT_MAT_X_P01_C06_E01_004_Q01##)'
Find the coordinates of its vertices.
View SolutionA large trapezium made up of four equal trapeziums:
'(##VPU_TTT_MAT_X_P01_C06_E01_005_Q01##)'
Find the coordinates of the vertices of all these trapeziums.
Drảw this picture in GeoGebra.
View SolutionIn the picture, the centre 'O' of the circle is the origin and 'A, B' are points on the circle.
'(##VPU_TTT_MAT_X_P01_C06_E01_006_Q01##)'
Calculate the coordinates 'A' and 'B'.
View SolutionWrite the coordinates of the points of a circle with centre as origin and radius '4.5' cuts the axes.
View SolutionA circle with centre '(2,0)' passes through the point '(-5,0):' Write the coordinates of other point.
View SolutionMark the coordinates of the point given below. Join in order. Find the peculiarity.
a) '(-2,2),(-1,1),(0,0),(1,-1),(2,-2)'
b) '(1,5),(2,9),(3,13),(4,17)'
c) '(3,4),(5,10),(7,16),(9,22)'
View Solution(4,9)' is a point on the circle with centre '(4,5) .' Write coordinates of another point on the circle.
View SolutionMark the points '(0,0),(1,1),(2,2)' '(-1,-1) .' What is the peculiarity of these numbers?
View SolutionMark the points where the y coordinates become.the double of 'x' - coordinate.
View SolutionIn the figure O is the centre and radius '5cm'. Find the coordinates of 'P'.
'(##VPU_TTT_MAT_X_P01_C06_E02_007_Q01##)'
View SolutionAll rectangles below have sides parallel to the axes. Find the coordinates of the remaining vertices of each.
'(##VPU_TTT_MAT_X_P01_C06_E03_001_Q01##)'
View SolutionWithout drawing coordinate axes, mark each pair of points below with left-right, top-bottom position correct. Find the other coordinates. of the rectangles drawn with these as opposite vertices and sides parallel to the axes.
i) '(3,5),(7 , 8)'.
ii) '(6,2),(5,4)'
iii) '(-3 , 5),(-7,1)'
iv) '(-1,-2),(-5,-4)'
View SolutionCalculate the length of the sides and diagonals of the trilateral below:
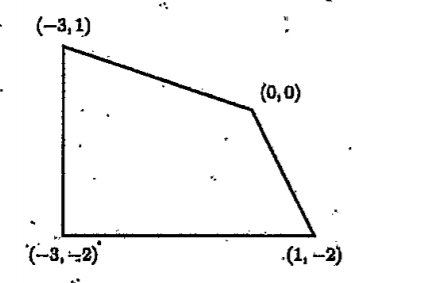
View SolutionProve that-by joining the points '(2,1)', '(3,4),(-3,6)' we get a right triangle.
View SolutionA circle of radius 10 is drawn with the origin as centre,
i) Check whether, each of the' points with coordinates '(6,9),(5,9),(6 , 8)' is inside, outside or on the circle.
ii) Write the coordinates of 8 points on this circle.
View SolutionFind the coordinates of the points where a circle of radius 'sqrt2', centred on the point with coordinates '(1,1)' cut the axes.
View SolutionThe coordinates of the vertices of a triangle are '(1,2),(2,3),(3,1)'. Find the coordinates of the centre of its circumcircle and the circumradius.
View SolutionProve that the triangle with vertexes '(0,0),(10,0)' and '(5,5 sqrt3)' is equilateral.
View SolutionProve that the points. '(3,-2),(7,6)', '(-1,2),(-5,-6)' form the vertices of a rhombus.
View SolutionProve that '(9,3),(7,-1),(1,-1)' are the points on the circle with centre '(4 , 3)'.
View Solution(2,5)' is the centre of a circle with radius '13 cm'. Classify the following points as points on the circle, points inside the circle and points outside the circle. '(13,13),(7,17),(12,13),(5,20)'
View SolutionFind the area of the rhombus ABCD with coordinates of its vertices are 'A(2, 0)', 'B(5,-5) , C(8,0)' and 'D(5,5)'
View SolutionFind the coordinates of the points of the circle of radius 5 and centre '(-2,3)', cut the 'x' -axis. Is.the point '(0,-6)' on the same circle? Examine.
View SolutionIf a circle is drawn with origin as centre ańd 5 radius, how many points having integers as the coordinates 'x' and 'y' on this circle?
View SolutionProve that the quadrilateral with vertices '(1,1),(5,1),(7,8),(3,8)' is a parallelogram.
View SolutionFind the area of the rhombus ABCD with coordinates of its vertices are 'A(2, 0)', 'B(5,-5) , C(8,0)' and 'D(5,5)'
View SolutionIn the figure C is the centre of the circle with radius 5 units. Circle is passing through the point 'A(8,0) . P C' is perpendicular to 'x' -axls. Find the coordinates of the points 'P, B' and 'C'.
'(##VPU_TTT_MAT_X_P01_C06_E05_010_Q01##)'
View SolutionIn the figure semicircle with diameter AB passes through the point 'P'. If 'A(-8 , 0)' and 'P(0,4)' then
'(##VPU_TTT_MAT_X_P01_C06_E05_011_Q01##)'
What is the length of OP?
What is the coordinates of B?
View SolutionA(1,2), B(6,4)' and 'C(8,9)' are the vertices of the parallelogram 'ABCD'. Find the co-ordinates of 'D'.
View SolutionA circle with centre as origin passes through the point '(6,0)'. a) Find the radius of the circle.
View Solutiona) Draw coordinate axes and mark the point '(2,4)'. Draw the circle of radius 4 units centred at the above point:
(b) Find the coordinates of the point:at which the circle cuts the 'x' axis.
(c) Calculate the coordinates of the point at which the circle cuts the 'y' axis.
View SolutionA(5,3)' is a point on a line parallel to 'x' axis.
a) Write the coordinates of any other point on the same line.
b) What is the distance of that (you have written) point from A?
View SolutionIn the figure, 'OABC' is a rectangle.
'A(12,0), C(0,5)' are two of its vertices.
'(##VPU_TTT_MAT_X_P01_C06_E08_002_Q01##)'
a) Write the coordinates of 'O & B'.
b) Find the length of OB.
View SolutionCoordinates of the end. points of a' diameter of a circle are '(1,3)' and '(11,3)'
a) Calculate the length of the diameter
b) Write the coordinates of the centre
c) Write the coordinates of any other point on the same circle
View Solutiona) Draw the 'x, y' axes and mark țe points 'A(-3,0), B(3,0)'
b) Construct an equilateral triangle ABC with AB as one of its sides.
c) Write' the coordinates of the third vertex of the equilateral triangle.
View SolutionIn the figure, 'BC' is paraliel to the 'x' axis. If the coordinates of 'A' is '(1,5)' and 'B' is, '(-2,1)' then,
'(##VPU_TTT_MAT_X_P01_C06_E08_005_Q01##)'
a) What is the length of 'A B' ?
b) Write the coordinates of 'C' if 'A C=sqrt(41)'
c) If 'AD'. is perpendicular to 'BC', then find the coordinates of D.
View SolutionIn the figure, the sides of the square are parallel to the axes and the origin is the midpoint. Coordinates of one vertex of the square is '(3,3)'.
'(##VPU_TTT_MAT_X_P01_C06_E09_001_Q01##)'
Write the coordinates of two other vertices of the square.
View SolutionThe centre of the circle is thé origin and the radius is 13.
a) . Check whether each of the points '(12,5),(10,6)' is inside, outside or on the circle.
b) Write the coordintes of two other points on the circle.
View SolutionIn the picture, mid points of the sides of the rilateral 'A B C D' are joined to draw PQRS.
'(##VPU_TTT_MAT_X_P01_C06_E09_003_Q01##)'
a) Find the coordinates of R.
b) Write coordinates. of all vertices of rilateral ABCD.
View Solutionlin the figure, 'O A B C' is a rectangle and its breadth is 3. Write the Co-ordinates of the vertices of 'B' and 'C'.
'(##VPU_TTT_MAT_X_P01_C06_E10_001_Q01##)'
View SolutionIn the figure, 'P(2,1), Q(3,3), R(1,2)' are the midpoints of the sides of the triangle 'ABC'.
'(##VPU_TTT_MAT_X_P01_C06_E10_002_Q01##)'
a) What type of the rilateral is PQCR?
b) Write the coordinates of the vertices A and C.
View SolutionA circle with, centre `(3,2)` passes through the point `(6,3)`.
a) What is the radius of the circle?
b) Check whether each of the points with coordinates
`(0 , 2),(3,6),(0,3)` is inside, outside or on the circle.
View SolutionA circle is drawn with the origin as centre. It passes through
the point `(3,3)`
a) What is the radius of the circle?
b) Write the coordinates of a point where the circle meets
the `X` - axis.
View SolutionDraw the coordinate axes and mark the points (4,0). Drawn an isosceles right angles triangle with this point as one of its vertcices.
View SolutionThe coordinates of two opposite vertices. of a rectangles are '(7,8)' and '(1,3):'
a) Without drawing coordinate axes, mark these points as the vertices of a rectangle with left-right, top-bottom positions correct.
b) Find the coordinates of other two vertices.
c) What is the length of its diagonals?
View SolutionIn the figure 'ABCD' is a parallelogram:
'/_ E=90^circ, A(3,5) , B(8,5)' are two vertices. 'BE=3' units, 'CE=4' units.
'a) Write the coordinates of 'C'.
b) What are the coordinates of D?
'(##VPU_TTT_MAT_X_P01_C06_E11_004_Q01##)'
c) Find the coordinates of meeting point of the diagonals of the paràllelogram.
View SolutionFind the coordinates of the point on `x` axis at a distance 4 units from (3,4).
View Solutiona) Draw the coordinate axes and mark, the points 'A(1,1), B(7,1)'
b) Draw an isosceles right triangle ABC with AB as hypotenuse.
c) Write the coordinates of 'C'.
View SolutionIn the figure, the sides of the square are. parallel to the axes and the origin is the midpoint. Coordinates of one vertex of the square is '(3,3)' : Write the coordinates of two other vertices of the square.
'(##VPU_TTT_MAT_X_P01_C06_E13_001_Q01##)'
View SolutionIn the figure 'Delta OAB' is an equilateral triangle. Find the coordinates of the vertex 'B'.
'(##VPU_TTT_MAT_X_P01_C06_E13_002_Q01##)'
View SolutionIn the figure, centre of the circle is 'C(3,0)' and radius is 3 units.
'(##VPU_TTT_MAT_X_P01_C06_E13_003_Q01##)'
a) Write the coordinates of the points 'A, B, P, Q'
b) Write the coordinate of another point on the circle.
c). Check whether the point '(0,5)' is inside the circle.
View SolutionWithout drawing coordinate axes mention the positions of 'A(2,1), B(6,1), C(6,5)' as left-right, above-below.
Draw coordinate axes, mark the points and complete triangle 'ABC'
Which side of the triangle is parallel to 'x' axis .
Which side is parallel to 'y' axis
Write the coordinates of the midpoint of AB.
Write the coordinates of the midpoint of BC.
Write the coordinates of the midpoint of AC.
View SolutionFind the coordinates of fourth vertices of the parallelogram.
'(##VPU_TTT_MAT_X_P01_C06_E13_005_Q01##)'
Find the length of the sides of the paralielogram.
Write the length of diagonals.
View Solution
QUESTION BANK questions and complete solutions for chapter COORDINATES of V PUBLICATION of Class 10