Complete Solutions to EXERCISE 8.2 of chapter SIMILAR TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILAR TRIANGLES |
| VGS PUBLICATION-BRILLIANT | EXERCISE 8.2 |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
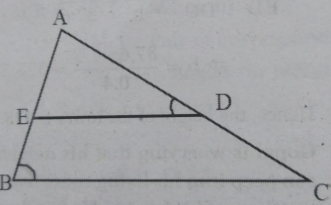
In the given figure `angle ADE=angleB`
Show that `DeltaABC~DeltaADE`.
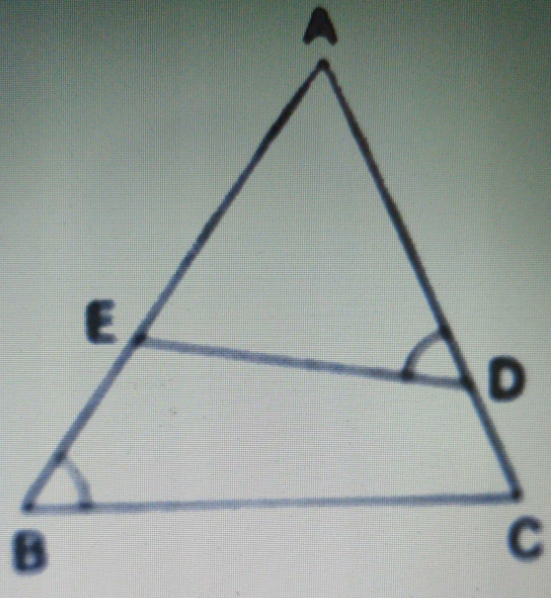
View SolutionIn the given figure `angle ADE=angleB`
IF AD=3.8 cm, AE=3.6 cm, BE=2.1 cm, BC=4.2 cm, find DE.
View SolutionThe perimeters of two similar triangle are 30 cm and 20 cm respectively. IF one side of the first Triangle is 12 cm. determine the corresponding side of the second Triangle.
View SolutionA girl of height 90 cm is walking away from the base of a lamp-post at a speed of `1.2m//sec`. IF the lamp-post is 3.6 m above the ground, find the length of her shadow after 4seconds.
View SolutionCM and RN are respectively the medians of similar triangle `DeltaABC` and `DeltaPQR`. Prove that
`DeltaAMC~DeltaPNR`
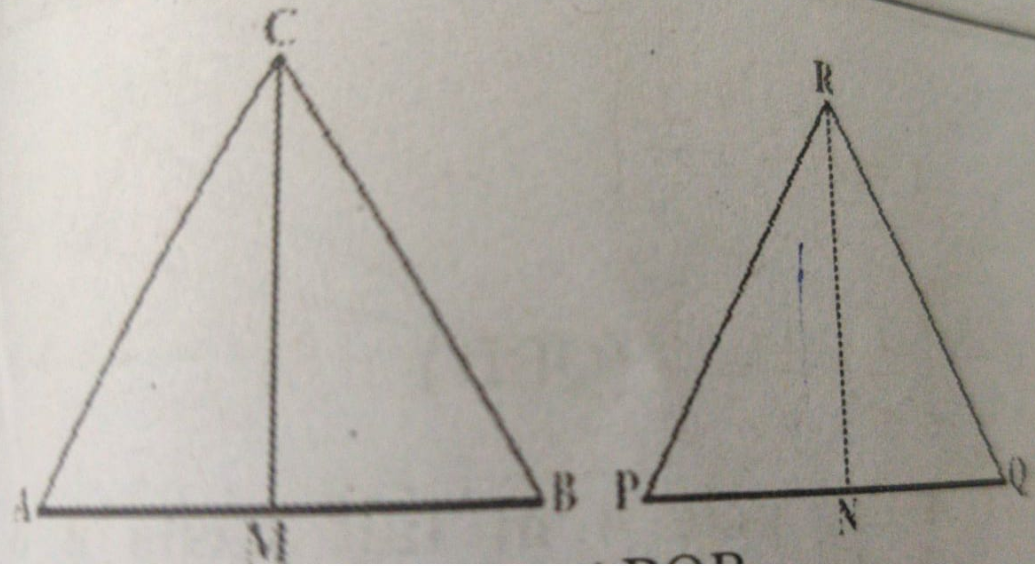
View SolutionCM and RN are respectively the medians of similar triangle `DeltaABC` and `DeltaPQR`. Prove that
`(CM)/(RN)=(AB)/(PQ)`

View SolutionCM and RN are respectively the medians of similar triangle `DeltaABC` and `DeltaPQR`. Prove that
`DeltaCMB~DeltaRNQ`
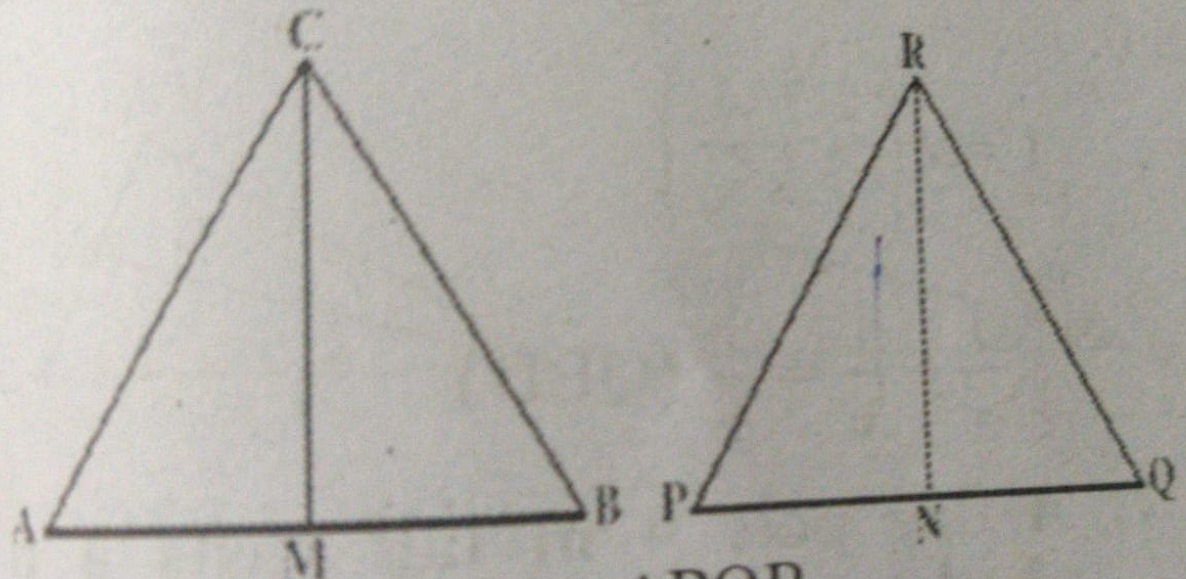
View SolutionDiagonals AC and BD of a trapezium ABCD with `AB||DC` intersect each other at the point 'O'.Using the criterion of similarity for two tri-angles , show that `(OA)/(OC)=(OB)/(OD)`.
View SolutionAB,CD,PQ are perpendicular to BD. AB=x. CD=y and PQ=z, prove that `1/x+1/y=1/z`.
View SolutionA flag pole 4 cm tall casts a 6m, shadow. At the same time , a nearby building casts a shadow of 24 m. How tall is the building?
View SolutionCD and GH are respectively the bisectors of `angle ACB` and `angle EGF` such that D and H lie on sides AB and FE of `DeltaABC and Delta FEG` respectively. IF `DeltaABC~DeltaFEG` then show that
`(CD)/(GH)=(AC)/(FG)`
View SolutionCD and GH are respectively the bisectors of `angle ACB` and `angle EGF` such that D and H lie on sides AB and FE of `DeltaABC and Delta FEG` respectively. IF `DeltaABC~DeltaFEG` then show that
`DeltaDCB~DeltaHGE`
View SolutionCD and GH are respectively the bisectors of `angle ACB` and `angle EGF` such that D and H lie on sides AB and FE of `DeltaABC and Delta FEG` respectively. IF `DeltaABC~DeltaFEG` then show that
`DeltaDCA~DeltaHGF`
View SolutionAX and DY are altitudes of two similar triangle `DeltaABC` and `DeltaDEF`. Prove that `AX:DY=AB:DE`.
View SolutionConstruct a Triangle shadow similar on the given `DeltaABC`, with its sides equal to `5/3` of the corresponding sides of the triangle ABC.
View SolutionConstruct a Triangle of sides 4 cm, 5 cm and 6cm. Then, construct a Triangle similar to it, whose sides are `2//3` of the corresponding sides of the first Triangle.
View SolutionConstruct is an isosceles Triangle whise base is 8 cm and altitude is 4 cm, Then, draw another Triangle whose sides are `1^1//2` times the corresponding sides of the isosceles Triangle.
View Solution
EXERCISE 8.2 questions and complete solutions for chapter SIMILAR TRIANGLES of VGS BRILLIANT MATHS (TELUGU ENGLISH) of Class 10
All Exercises from VGS PUBLICATION-BRILLIANT Class 10 MATHS SIMILAR TRIANGLES
- (PART-A) OBSERVATION MATERIAL TO SOLVE VARIOUS QUESTION GIVEN IN THE PUBLIC EXAMINATION (1 MARK QUESTION)
- (PART-A) OBSERVATION MATERIAL TO SOLVE VARIOUS QUESTION GIVEN IN THE PUBLIC EXAMINATION (2 MARK QUESTION)
- (PART-A) OBSERVATION MATERIAL TO SOLVE VARIOUS QUESTION GIVEN IN THE PUBLIC EXAMINATION (4 MARK QUESTION)
- CREATIVE BITS FOR CCE MODEL EXAMINATION
- CREATIVE QUESTION FOR CCE MODEL EXAMINATION
- EXAMPLES
- EXERCISE 8.1
- EXERCISE 8.2
- EXERCISE 8.3
- EXERCISE 8.4
- OBSERVATION BITS TO SOLVE VARIOUS BITS IN THE GIVEN IN THE PUBLIC EXAMINATION
- OPTIONAL EXERCISE
- TRY THIS