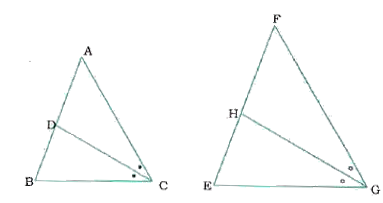
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFGSolution in Telugu
Step by step video & image solution for CD and GH are respectively the bisectors of angle ACB and angle EGF such that D and H lie on sides AB and FE of DeltaABC and Delta FEG respectively. IF DeltaABC~DeltaFEG then show that (CD)/(GH)=(AC)/(FG) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE 8.3
8 Videos
- SIMILAR TRIANGLES BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE 8.4
12 Videos
- SIMILAR TRIANGLES BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE 8.1
9 Videos
- SETS BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SETS EXERCISE - CREATIVE BITS OF CCE MODEL EXAMINATION
116 Videos
- STATISTICSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - STATISTICSEXERCISE - EXERCISE
146 Videos
Similar Questions
Equilateral triangle are drawn on the three sides of a right angled Triangle. Show that the area of the Triangle on the hypotenuse is equal to the sum of the areas of triangle on the other two sides.
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
View SolutionIn ΔPQR,ST is a line such that PSSQ=PTTR and also ∠PST=∠PRQ. Prove that ΔPQR is an isosceles Triangle.
View SolutionLet A={1,2,{1},{1,2},3,4}, then which of the following is true?
View SolutionThe mean value can be calculated from both ungrouped and grouped date . Which one you think is more accurate ? Why ?
View SolutionIn the given figure, CD and GH are respectively the bisectors of angle ACB and angle FGE "of" Delta ABC and Delta EFG respectively . If Delta ABC~ Delta FEG , prove that : (a) Delta ADC~ Delta FHG " " (b) Delta BCD ~ Delta EGH " " ( c ) (CD)/(GH)=(AC)/(FG)
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
View Solution
