Complete Solutions to MODEL EXAMINATION of chapter APPLICATIONS OF TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | APPLICATIONS OF TRIGONOMETRY |
| VGS PUBLICATION-BRILLIANT | MODEL EXAMINATION |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
The length of the shadow of a tree is 8 m long when the sun's angle of elevation is `45^(@)` is………….m.
View SolutionIf a pole 6 m high casts a shadow `2sqrt(3)`m long on the ground. Then the sun's angle of elevation is
View SolutionIf the angle of elevation of a tower from a distance of 100 m from its foot is `60^(@)`. Then the height of the tower is ……….m.
View SolutionThe height of a tower is 10m. The length of its shadow when sun's altitude is `45^(@)` is……….m.
View SolutionThe length of the shadow of a tower on the plane ground is `sqrt(3)` times the height of the tower. The angle of elevation of sun is
View SolutionIn the given figure, the position of the observer and the object are marked, the angle of depression is

View SolutionIn the given, the value of angle `theta` is
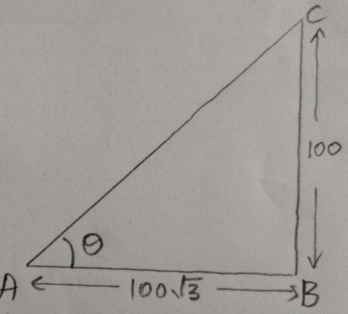
View SolutionThe ratio of the length of a rod and its shadow is `1:sqrt(3)`, then the angle of elevation of the sun is
View SolutionIf two towers of height X and Y subtend angles of `30^(@)" and "60^(@)` respectively at the centre of the line joining their feet, then X:Y is equal to
View SolutionA wall of 8m long casts a shadow 5m long. At the same time, a tower casts a shadow 50m long. Then the height of tower is
View SolutionIf the sun's angle of elevation is `60^(@)`. Then a pole of height 6m will cast a shadow of length……….m.
View SolutionA pole of 12m high casts a shadow `4sqrt(3)`m on the ground. Then the sun's angle of elevation is
View SolutionIf the height and length of the shadow of a man are the same, then the angle of elevation of the sun is
View SolutionThe given figure shows the observation of point 'C' from point A. The angle of depression from A is

View SolutionIf the length of the shadow of a tower is `(1)/(sqrt(3))` times the height of the tower, then the angle of elevation of the sun is………
View SolutionA tower is 50m high. Its shadow is x m shorter when the sun's altitude is `45^(@)` then when it is `30^(@)`, then x=……….m.
View SolutionThe length of the string of a kitef flying at 100m above the ground with the elevation of `60^(@)` is…………..
View SolutionA player sitting on the top of a tower of height 40m observes the angle of depression of a ball lying on the ground is `60^(@)`. The distance between the foot of the tower and ball is…………m.
View SolutionIf the ratio of height of a tower and the length of its shadow on the ground is `sqrt(3):1`, then the angle of elevation of the sun is…………
View SolutionThe angle of depression from the top of a tower 100m height, at a point on the ground is `45^(@)`,. The distance of the point from the tower is…………….
View SolutionAn object is placed above the observer's horizontal, we call the angle between the line of sight and observer's horizontal is………
View SolutionAngle of elevation of the top of a building from a point on the ground is `30^(@)`, Then the angle of depression of this point from the top of the building is…………..
View SolutionWhat change will be observed in the angle of elevation as we move away from the object?
View SolutionAn objcet is placed below the observer's horizontal, then what is the angle between line of sight and observer's horizontal ?
View SolutionWhat change will be observed in the angle of elevation as we approach the foot of the tower?
View SolutionIn the figure given below, the imaginary line through the object and eye of the observer is called………..

View SolutionIn the figure given below, a man on the top of cliff observers a boat coming towards him. Then `theta` represents the angle of…………….

View SolutionIn the figure given below, if AB=10m and AC=20m, then `theta` =…………….
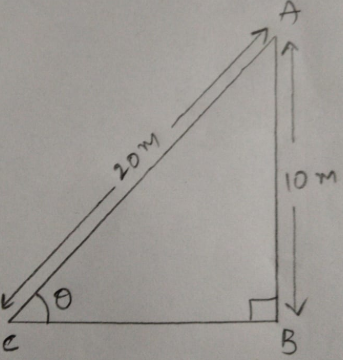
View SolutionIf a pole height 6m casts a shadow `2sqrt(3)`m long on the ground, then the sun's elevation is
View SolutionIn figure given below, if AB=CD=`10sqrt(3)` m then BC=………….m.
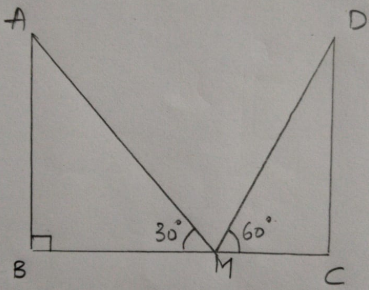
View SolutionIn the figure given below, if AB=`10sqrt(3)`m, then CD=……….
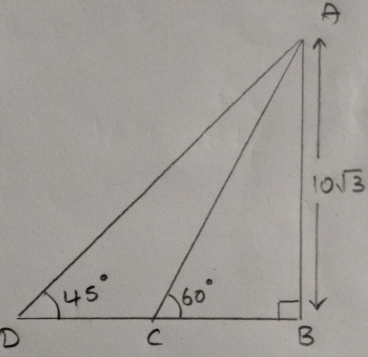
View SolutionIn the figure given below, if AD=`7sqrt(3)`m, then BC=………m.
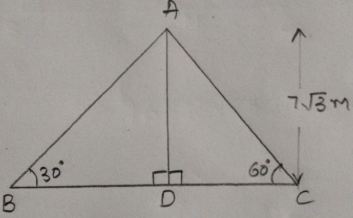
View SolutionThe length of the shadow of a tree is 7m and height is 7m, when the sun's elevation is………….
View SolutionIf two tangents inclined at an angle of `60^(@)` are drawn to a circle of radius 3 cm, then length of tangents is equal to…………m.
View SolutionThe angle formed by the line of sight with horizontal, when the point being viewed is above the horizontal level is called……….
View Solution`cot^2 B-cosec^2 B`=………….
View Solution`(tan theta)/(sec theta)`=…………….
View SolutionA boy observed the top of an electrical pole to be at angle of elevation of `60^(@)` when the observation point is 8m away from the foot of the pole then the height of the pole is……….m.
View SolutionSuppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of `60^(@)`. What is the distance between you and the object ?
View Solution`sin""(pi^e)/(2)`=…………
View SolutionDomain of `sin theta`=………….
View Solution`tan""(pi^e)/(4)`=…………..
View Solution`cot 15^(@)`=……………..
View Solution`A+B=180^(@)` then `cosA+cos B`=………..
View Solution`sin 15^(@)`=………….
View Solution`tanA=(n)/(n+1), tanB=(1)/(2n+1), tan(A+B)`=………..
View SolutionThe angle of elevation of tower at a point 40m apart form it is `cot^(-1)(3/5)`. Obtain the height of the tower.
View SolutionA ladder 20m long is placed against a vertical wall of height 10m, then the distance between the foot of the ladders and wll is………m.
View Solution`sin 18^(@)`=…………
View SolutionIn the below figure x=……
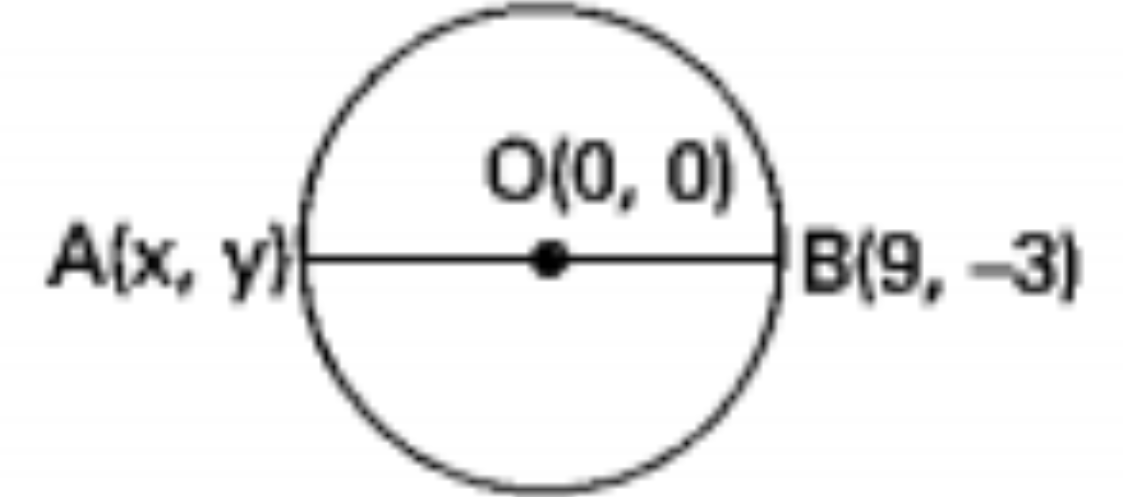
View Solution` cot(90-A)=`…………….
View Solution`cos^4""A-sin^4 A`=…………
View SolutionIf `cosec theta+cot theta =k" then "cos theta`=………….
View Solution`x=(sec theta+tan theta),y=(sec theta-tan theta)` then xy=…………
View Solution`tan 15^(@)`=………….
View Solution`cosec theta`=………..
View Solution`x=a sin theta, y=a cos theta " then "x^2+y^2`=…………
View SolutionExample of a Pythagorean Triplet is…………
View Solution`sec^2 A`=…………..
View Solution`(1)/(cos theta)-cos theta`=………….
View Solution`sin theta=cos theta,theta in Q_1` then `theta`-
View Solution`72^(@)`=…………….
View Solution`sin^2""105^(@)+cos^2""105^(@)`=…………..
View Solution`sin 45^(@)(cos 45^(@))`=…………..
View Solution`cos 40^(@)=0.76` then `sin 50^(@)`=………….
View SolutionAt a point 15m away form the base of a 15m high pole, the angle of elevation of the top is……….
View SolutionThe length of shadow of a pole is equal to the length of the pole, then the angle of the elevation of the Sun is …………
View SolutionThe angle of elevation of top of a tree is `30^(@)`. On moving 20m nearer, the angle of elevation is `60^(@)`. The height of the tree is
View SolutionThe ratio of length of a pole and its shadow is `1:sqrt(3)`. The angle of elevation is
View SolutionThe upper part of a tree is broken by wind and makes an angle of `30^(@)` with the ground and at a distance of 21m from the foot of the tree. Find the total height of the tree.
View SolutionFrom a bridge 25m high, the angle of depression of a boat is `45^(@)`. Find the horizontal distance of the boat from the bridges.
View SolutionA tower makes an angle of elevation equal to the angle of depression from the top of a cliff 25m height. Find the heigh of the tower.
View SolutionWhen the angle of elevation of a pole is `45^(@)`, the length of the pole and its shadow are
View SolutionIn a rectangle, if the angle between a diagonal and a side is `30^(@)`, and the length of the diagonal is 6 cm, the area of the rectangle is
View SolutionTwo posts are 15 m and 25m high and the line joining their tope make an angle of `45^(@)` with the horizontal, the distance between the two posts is
View SolutionAn electric pole 20m high stands up right on the ground with the help of steel wire to its top and affixed on the ground. If the steel wire makes `60^(@)` with the horizontal ground, find the length of steel wire.
View SolutionA building casts a shadow of length `50sqrt(3)` m when the sun is `30^(@)` about the horizontal. The height of the building is
View SolutionWhen the angle of elevation of a light changes from `30^(@)" to "45^(@)`, the shadow of pole becomes `100sqrt(3)` m less. The height of the pole is
View SolutionFrom the top of a building 50m from horizontal, the angle of depression made by a car is `30^(@)`. How far is the car from the building?
View SolutionFrom the top of a building with height `30(sqrt(3)+1)`m two cars make angle of depression of `45^(@)" and "30^(@)` due east. What is the distance between two cars?
View SolutionA person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is `60^(@)`. When he retires 40m from the bank, he finds the angle to be `30^(@)`. The breadth of the river is
View SolutionA ladder touches a wall at a height of 5m. The angle made by the ladder with the ground, if its length is 10m, will be………….
View SolutionA tree breaks due to storm and the broken part bends so that the top of the tree touches the ground by making `30^(@)` angle with the ground. The distance between the top of the tree and the ground is 10m. Find the height of the tree.
View SolutionIf the angle of elevation of a cloud from a point 200 m above a lake is `30o` and the angle of depression of its reflection in the lake is `60o` , then the height of the cloud above the lake, is (a) 200 m (b) 500 m (c) 30 m (d) 400 m
View SolutionAn aeroplane flying horizontally 1 km above the ground is observed at an elevation of `60^(@)`. After a flight of 10 seconds, its angle of elevation is observed to be `30^(@)` from the same point on the ground. Find the speed of the aeroplane.
View SolutionIf AB=4m, and AC=8m, then the angle of elevation of A as observed from C is
View SolutionIf a pole height 6m casts a shadow `2sqrt(3)`m long on the ground, then the sun's elevation is
View SolutionThe length of shadow of a pole is equal to the length of the pole, then the angle of the elevation of the Sun is …………
View SolutionIf the shadow of a tree is `(1)/(sqrt(3))` times the height of the tree, then the angle of elevation of the sun is
View Solution
MODEL EXAMINATION questions and complete solutions for chapter APPLICATIONS OF TRIGONOMETRY of VGS BRILLIANT MATHS (TELUGU ENGLISH) of Class 10