Complete Solutions to SECTION A of chapter CBSE BOARDS 2020 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CBSE BOARDS 2020 |
| 2020 | SECTION A |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
For the following frequency distibution .

View SolutionWhat is the probability of an impossible event?
View SolutionIf `(3,-6)` is the mid-poiint of the line segment joing `(0,0) and (x,y),` then the point `(x,y)` is
View SolutionThe discriminant of the quadratic equation `4x^(2) -6x+3=0 ` is
View SolutionIn the given circle if Figure-1, number of tangents parallel to tangents PQ is

View Solution`8cot ^(2) A-8 cosec ^(2)A ` is equal to
View SolutionThe point on x-axis which divides the line segment joining `(2,3)` and `(6,-9)` in the ratio `1:3` is
View SolutionIf a pair of linear equations is consistent then the lines represented by then are
View SolutionThe total surface area of a frustum-shaped glass nuber is `(r_(1)gtr_(2))`
View Solution`120` can be expressed as a product of its prime factors as
View SolutionArea of quadrilateral ABCD =Area of `Delta ABC+` area of `"_______"`
View Solutionif the radii of two spheres are in the ratio `2:3`, then the ratio of their respective volumes is -----------------.
View SolutionIf 2 is a zero of the polynomial `ax^(2)-2x,` then the value of `a` is `"______"`
View SolutionA line intersecting a sirrcle in two points is called a `"_____"`
View SolutionAll squares are
View SolutionA dice is thrown once, If getting a six, is a success, then find the probability of a failure.
View SolutionFind the value of x so that `-6, x, 8` are in AP
View SolutionFind the `11^(th)` term of the A.P. `-27, -22, -17, -12,…`
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is `60^(@)` . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.

View SolutionEvaluate :
`tan 40^(@)xxtan 50^(@)`
View SolutionIf `cos A= sin 42^(@),` then find the value of A.
View SolutionFind the height of a cone of radius 5 cm and slant height 13 cm.
View SolutionThe value(s) of k for which the qudratic equation `2x^(2)+kx+2=0` has equal roots, is
View SolutionWhich of the followig is not an A.P?
View SolutionThe radius of a sphere (in cm) whose volume is 12`pi` `cm^3`, is
(A) 3
(B) 3 `sqrt(3)`
(C) `3^2/3`
(D) `3^1/3`
View SolutionThe distance between the points (m,-n) and (-m,n) is
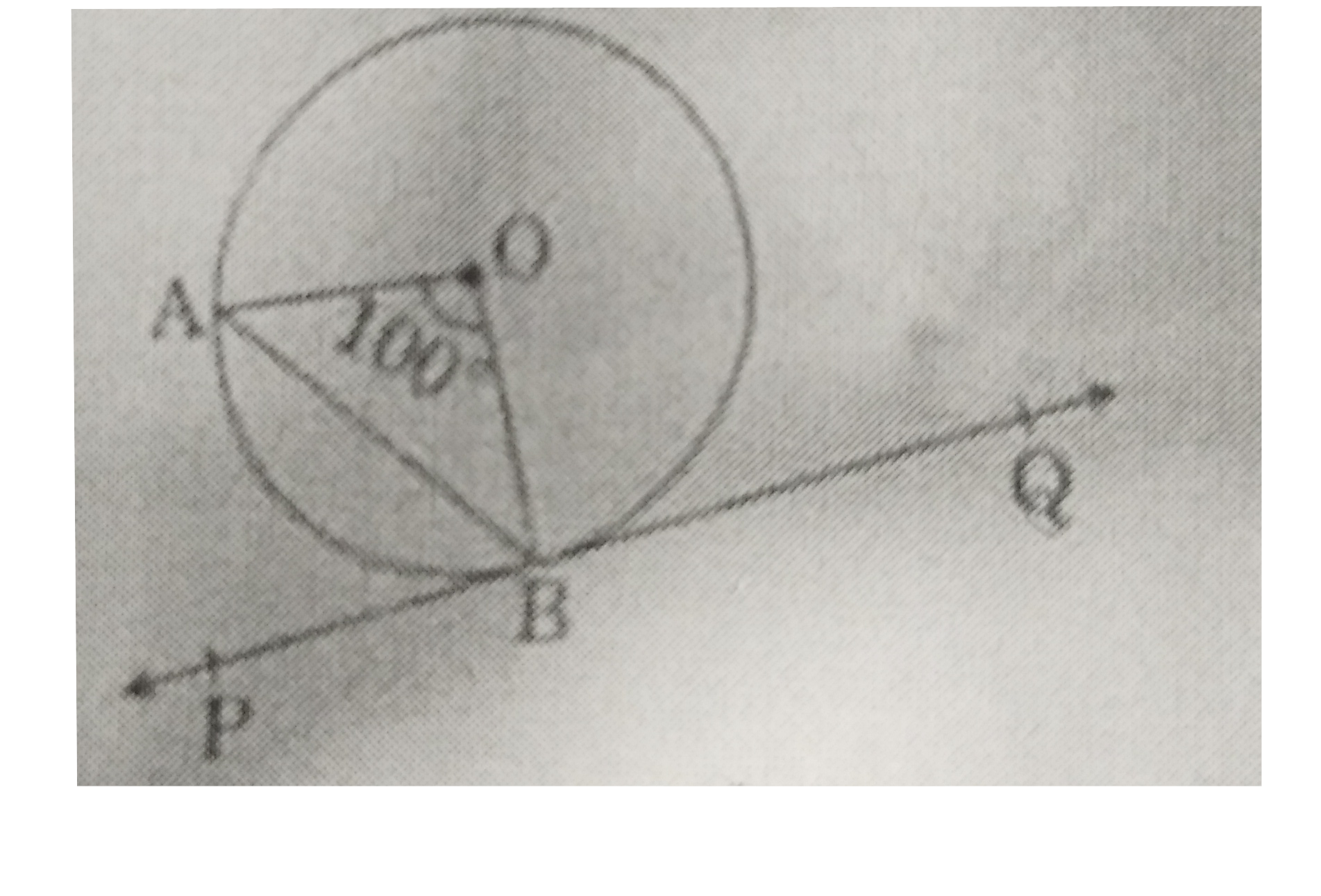
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if `angleQPR=90^(@)`, then length of PQ is
View SolutionOn dividing a polynomial p(x) by `x^2`- 4, quotient and remainder are found to be x and 3 respectively. The polynomial p(x) is
View SolutionIn figure-2, `DE||BC`. If `(AD)/(DB)=(3)/(2)` and `AE=2.7` cm then `EC` is equal to
View SolutionThe point on the axis which is equidistant from (-4,0) and (10,0) is ,
a) (7,0)
(b) (5,0)
c) (0,0)
d) (3,0)
View SolutionThe centre of a circle whose end points of a diameter are (-6,3) and (6,4)
a) (8,-1)
b) (4,7)
c) (0,`7/2`)
d) (4,`7/2`)
View Solutionthe pair of linear equations
3x/2+5y/3 =7 and 9x + 10y =14 is
(a) consistent
(b) inconsistent
(c) consistent with one solution
(d) consistent with many solutions
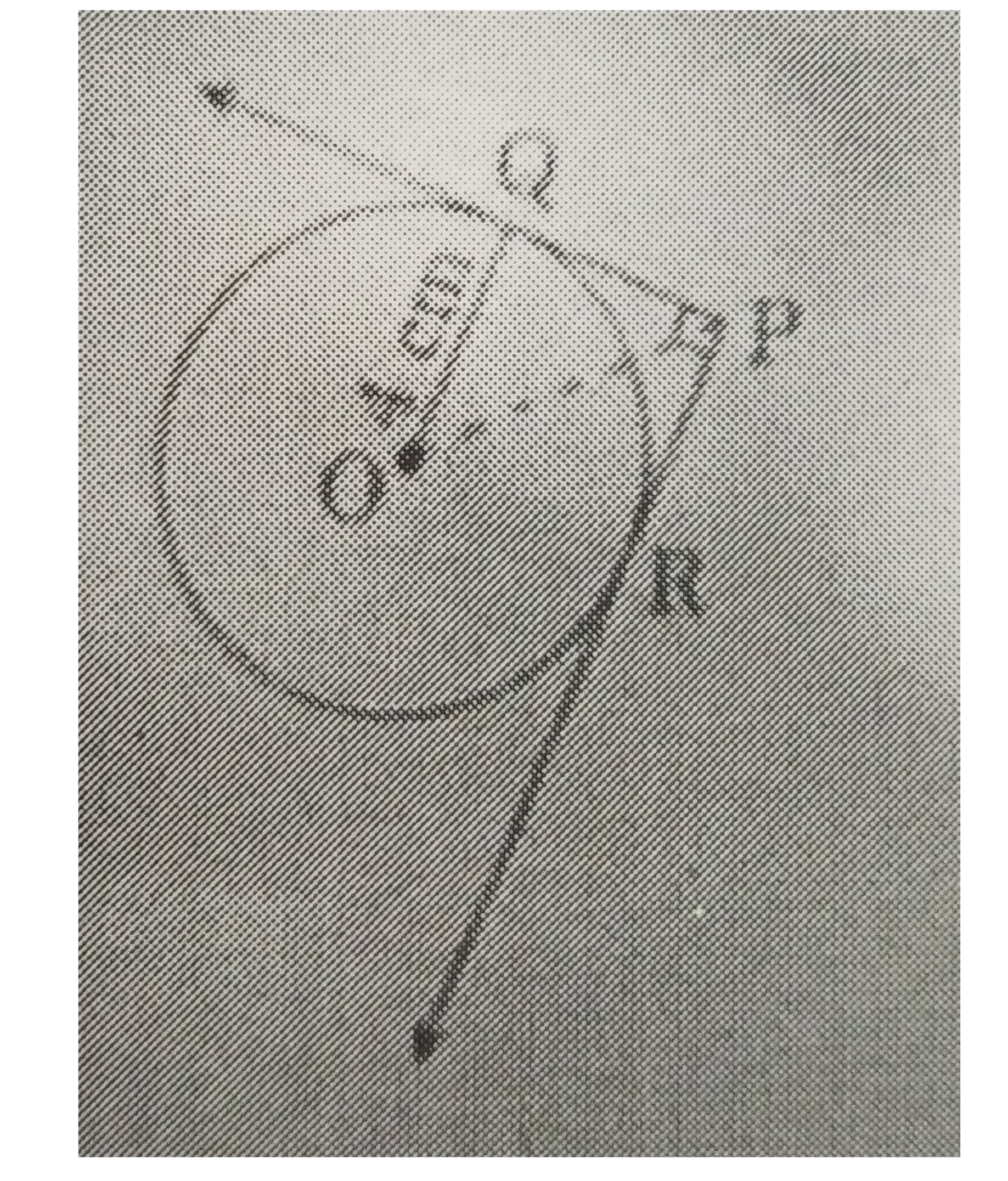
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if `angleAOB=100^(@)`, then `angleABP` is equal to
View SolutionSimplest form of (1+ `tan^2`A)/(1+`cot^2'A) IS
View SolutionIf the probability of an event E happening is 0.023, then `P(overline(E))`=______
View SolutionAll concentric circles are..... to each other.
View SolutionThe probability of an event that is sure to happen, is_____
View SolutionAOBC is a rectangle whose three vertices are A(0,-3), O(0,0) and B (4,0). The length of its diagonal is__
View SolutionWrite the value of `sin^(2)30^(@)+cos^(2)60^(@)`.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are `-3` and `2`, respectively.
View SolutionCan `(x^2 - 1)` be a remainder while dividing `x^4 - 3x^2 + 5x -9 by `x^2 + 3` justify your amswer with reasons.
View SolutionFind the sum of the first 100 natural numbers.
View SolutionThe LCM of two numbers is `182` and their HCF is `13`. If one of the numbers is `26`, find the other.
View Solution
If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is `30^(@)`. Find th height of the tower.
View Solution
SECTION A questions and complete solutions for chapter CBSE BOARDS 2020 of X BOARDS of Class 10