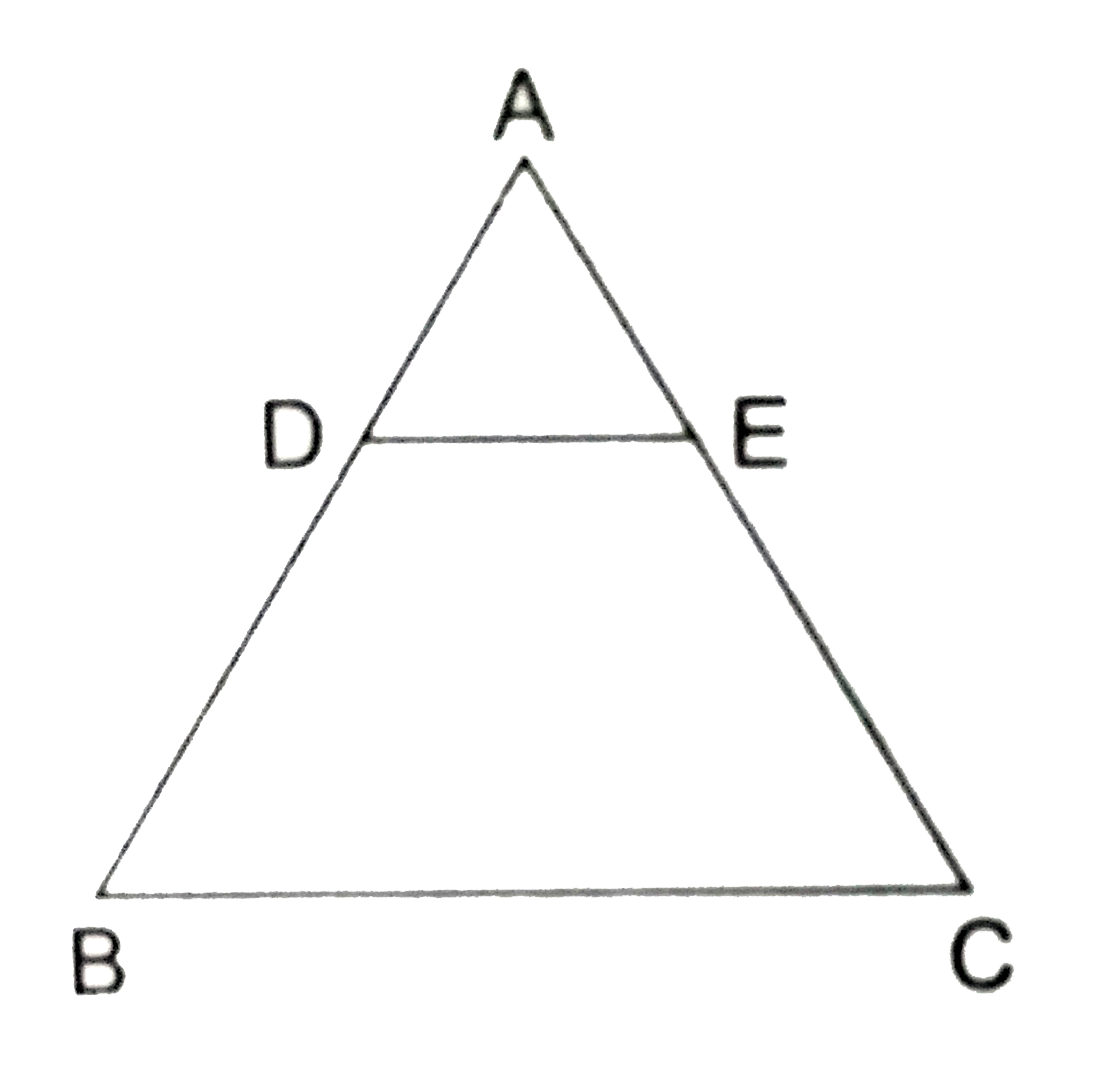
In figure-2, DE∣∣BC. If ADDB=32 and AE=2.7 cm then EC is equal to
2.0 cm
1.8 cm
4.0 cm
2.7 cm
The correct Answer is:B
To solve the problem step by step, we will use the Basic Proportionality Theorem (BPT).
1. Understand the Given Information:
- We have two segments, AD and DB, with a ratio of ADDB=32.
- The length of AE is given as 2.7 cm.
- We need to find the length of EC.
2. Use the Basic Proportionality Theorem (BPT):
- According to BPT, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- Therefore, we can write:
ADAB=AEAC
- Here, AB=AD+DB. Since AD:DB=3:2, we can express this as:
AD=3xandDB=2x
- Thus, AB=AD+DB=3x+2x=5x.
3. Substituting into the Proportionality Equation:
- Now we can substitute into the BPT equation:
ADAB=3x5x=35
- This gives us:
35=AEAC
4. Substituting the Known Value of AE:
- We know AE=2.7 cm, so we substitute that into the equation:
35=2.7AC
5. Cross-Multiplying to Solve for AC:
- Cross-multiplying gives:
3⋅AC=5⋅2.7
- Therefore:
AC=5⋅2.73
- Calculating this:
AC=13.53=4.5 cm
6. Finding EC:
- We know that:
AC=AE+EC
- Rearranging gives:
EC=AC−AE
- Substituting the values we found:
EC=4.5−2.7=1.8 cm
Final Answer:
Thus, the length of EC is 1.8 cm.
- We have two segments, AD and DB, with a ratio of ADDB=32.
- The length of AE is given as 2.7 cm.
- We need to find the length of EC.
- According to BPT, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- Therefore, we can write:
ADAB=AEAC
- Here, AB=AD+DB. Since AD:DB=3:2, we can express this as:
AD=3xandDB=2x
- Thus, AB=AD+DB=3x+2x=5x.
- Now we can substitute into the BPT equation:
ADAB=3x5x=35
- This gives us:
35=AEAC
- We know AE=2.7 cm, so we substitute that into the equation:
35=2.7AC
- Cross-multiplying gives:
3⋅AC=5⋅2.7
- Therefore:
AC=5⋅2.73
- Calculating this:
AC=13.53=4.5 cm
- We know that:
AC=AE+EC
- Rearranging gives:
EC=AC−AE
- Substituting the values we found:
EC=4.5−2.7=1.8 cm
Thus, the length of EC is 1.8 cm.
Similar Questions
Knowledge Check
In ΔABC,DE∣∣BCsuch that ADBD=35. If AC=5.6cm, then AE is equal to
A4.2 cm.B3.1 cm.C2.8 cm.D2.1 cm.In figure, DE∣∣BC and BD = 7.2 cm , CE = 5.4 cm and AE = 1.8 cm. Then AD is equal to :
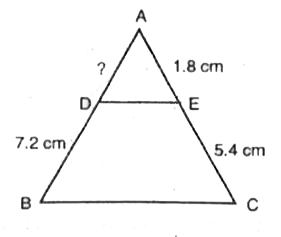 A4.2 cmB3.5 cmC2.4 cmDNone of these
A4.2 cmB3.5 cmC2.4 cmDNone of theseIn thegiven figure, if DEBC=23 and if AE = 10 cm. Find AB :
 A16 cmB12 cmC15 cmD18 cm
A16 cmB12 cmC15 cmD18 cm
In ΔABC,DE∣∣BC such that ADDB=35 . If AC=5.6cm then, AE=?
View SolutionIn a given figure if DEBC=23 and if AE = 12 then find AB.
View SolutionIn the given figure, DE∣∣BC. If DE=5cm,BC=8cmandAD=3.5cm then AB=?
View SolutionIn the given figure, DE || BC. If AB = 12 cm and AD = 3cm, then AE : EC =
View SolutionIn triangle ABC, DE∣∣BCandADDB=3(5) . If AC = 4.8 cm .Find AE.
View Solution