Complete Solutions to ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE 1 - QUESTIONS) of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| ZEN PUBLICATION | ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE 1 - QUESTIONS) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
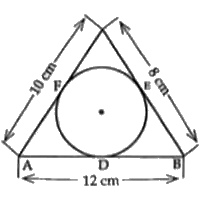
In the given figure, a circle is inscribed in a `DeltaABC` such that it touches the sides AB, BC, and CA at points D, E, and F respectively. If the lengths of the sides AB, BC, and CA are 12 cm, 8 cm, and 10 cm respectively, find the lengths of AD, BE, and CF.
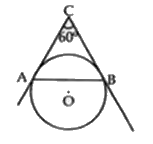
View SolutionIn the given figure, AP and BP are tangents to a circle with centre O such that `AP=5 cm` and `|__APB=60^(@)`. Find the length of chord AB.
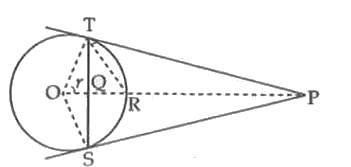
View SolutionIn the given figure, from an external point P, two tangents PT and PS are drawn to the circle with centre O and radius r. If `PO=2r`, show that `|__OTS= |__OST=30^(@)`.
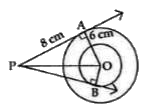
View SolutionIn the given figure, there are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and the length of `AP=8cm`, find BP
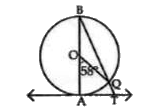
View SolutionIn the figure, AB is the diameter of a circle with centre O and AT is a tangent. If `|__AOQ=58^(@)`, find `|__ATQ`.
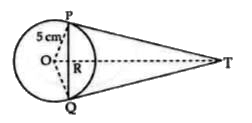
View SolutionIn the figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at T. Find TP and TQ.
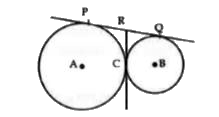
View SolutionIn the given figure, two circles touch each other externally at the point C. Prove that the common tangent to the circle at C bisects the common tangents at P and Q.
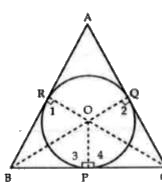
View SolutionIn the figure, an isosceles triangle ABC with `AB=AC` circumscribes a circle. Prove that the point of contact P bisects the base BC.
View SolutionIf `d_(1)` and `d_(2) (d_(2) gt d_(1))` be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, prove that `d_(2)^(2)=c^(2) + d_(1)^(2)`.
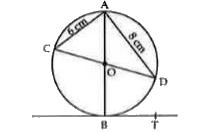
View SolutionIn the adjoining figure, `AD=8 cm, AC=6cm`, and TB is the tangent at B to the circle with centre O. Find OT if BT is 4 cm
View SolutionThe incircle of an isosceles triangle ABC in which `AB=AC`, touches the sides BC, CA, and AB at D, E, and F respectively. Prove that `BD=DC`.
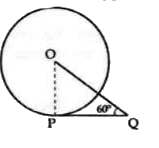
View SolutionIn the figure, PQ is a tangent of length 6 cm to the circle with centre O and `|__OQP=60^(@)`. Find OQ.
View SolutionIn the figure, PQ is a chord of a circle and PT is the tangent at P such that `|__QPT=60^(@)`. Find `|__PRQ`.

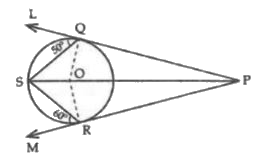
View SolutionIn the figure, PQL and PRM are tangents to the circle with centre O at the points Q and R respectively and S is a point on the circle such that `|__SQL=50^(@)` and `|__SRM=60^(@)`. Find `|__QSR`.
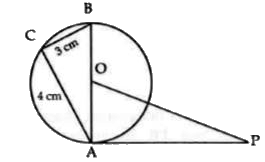
View SolutionPA is a tangent to the circle with centre O. If `BC= 3 cm, AC = 4 cm`, and `DeltaACB=DeltaPAO`, find OA and `(OP)/(AP)`.
View SolutionTwo circles with centre at A and B touch each other at C. Common tangents PQ and RC are drawn. If `|__PAC=50^(@)`, find `|__PRC` and `|__CBQ`.

View Solution
ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE 1 - QUESTIONS) questions and complete solutions for chapter CIRCLES of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS CIRCLES
- ILLUSTRATIVE EXAMPLE
- TEXTUAL ( Exercise 4.1 )
- TEXTUAL ( Exercise 4.2 )
- ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
- ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
- ZEN ADDITIONAL QUESTIONS ( LONG ANSWER [LA] TYPE - QUESTIONS)
- ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE - 2 - QUESTIONS)
- ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE 1 - QUESTIONS)
- ZEN ADDITIONAL QUESTIONS (MCQs)
- ZEN ADDITIONAL QUESTIONS (VERY SHORT ANSWER [VSA] TYPE QUESTIONS)